【数据结构】实验十:哈夫曼编码
实验十 哈夫曼编码
一、实验目的与要求
1)掌握树、森林与二叉树的转换;
2)掌握哈夫曼树和哈夫曼编码算法的实现;
二、 实验内容
1. 请编程实现如图所示的树转化为二叉树。
2. 编程实现一个哈夫曼编码系统,系统功能包括:
(1) 字符信息统计:读取待编码的源文件SourceFile.txt,统计出现的字符及其频率。
附:SourceFile.txt文件内容为
![]()
(2) 建立哈夫曼树:根据统计结果建立哈夫曼树。
(3) 建立哈夫曼码表:利用得到的哈夫曼树,将各字符对应的编码表保存在文件Code.txt中。
(4) 对源文件进行编码:根据哈夫曼码表,将SourceFile.txt中的字符转换成相应的编码文件ResultFile.txt。
实现提示:
(1) 字符信息统计:假设源文件SourceFile.txt中的字符只有大小写英文字母(同一个字母的大小写看作一个字符),则字符统计算法的实现过程可以归纳为:先定义一个含有26个元素的整形数组,用来存储各个字母出现的次数,最后还要排除其中出现次数为0的数组元素。
(2) 建立哈夫曼树:可参考教材算法。
(3) 建立哈夫曼码表:可参考教材算法。
(4) 对源文件进行编码:依次读入文件SourceFile.txt中的字符 c,在编码表 HC 中找到此字符,将字符c转换为编码表中存放的编码串,写入编码文件ResultFile.txt中,直到所有的字符处理完毕为止。
三、实验结果
1)请将调试通过的运行结果截图粘贴在下面,并说明测试用例和运行过程。
2)请将源代码cpp文件压缩上传。
题目1:
测试用例及运行结果:
测试用例输入的树为:
树通过孩子兄弟表示法转化的二叉树为:
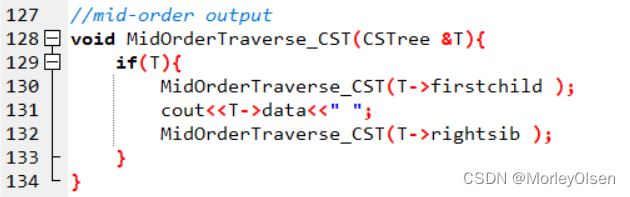
测试用例实验结果为:
根据最后三行输出(即二叉树的先序遍历和中序遍历,以及树的层序遍历)可知,输入的树可以转化为二叉树,且存储效果均良好。
运行过程:
首先通过主函数调用的函数顺序可知,运行过程为初始化树->通过输入创建树->preorder输出树->midorder输出树->floororder输出树->销毁树。
初始化树时,不需要做额外操作。
通过输入创建树时,主要使用队列实现。首先初始化每个结点的左孩子和右兄弟均为空,然后把当前结点加入队列。如果当前结点为根结点,则树从当前结点开始。否则,获取队列的队首结点,依次存储其左孩子和右兄弟。
preorder输出树时,通过if条件判断当前结点是否为空,然后采用根结点——左孩子——右兄弟的方法递归输出。
midorder输出树时,通过if条件判断当前结点是否为空,然后采用左孩子——根结点——右兄弟的方法递归输出。
floororder输出树时,主要通过队列输出。通过if条件判断当前结点是否为空,输出当前根结点的值,然后进行根结点排队。当队列非空时,先输出根结点e的左孩子p,再输出p的右兄弟,此时容易知道p和p的右兄弟在同一层。
销毁树时,通过if条件判断当前结点是否为空,然后采用左孩子——右兄弟——根结点的方法递归销毁,并依次将结点置为空。
实验代码:
//孩子兄弟表示法存储
#include
#include
#include
using namespace std;
typedef int ElemType;
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild,*rightsib;
}CSNode,*CSTree;
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef struct QNode{
CSTree data;
struct QNode *next;
}QNode;
typedef struct LinkQueue{
QNode *front,*rear;
}LinkQueue;
//构造空队列
void InitQueue_Sq(LinkQueue &Q){
Q.front = Q.rear = NULL;
}
//判断是否为空
int QueueEmpty(const LinkQueue &Q){
return (Q.rear == NULL && Q.front == NULL);
}
//插入元素进队尾
void EnQueue_Sq(LinkQueue &Q,CSTree &e){
QNode *p=(QNode*)malloc(sizeof(QNode));
if(!p){
exit(0);
}
p->data =e;
p->next =NULL;
if (QueueEmpty(Q)){
Q.front =Q.rear =p;
}
else{
Q.rear->next =p;
Q.rear=p;
}
}
//删除元素从队头
CSTree DeQueue_Sq(LinkQueue &Q,CSTree &s){
if(QueueEmpty(Q)){
return ERROR;
}
QNode *p=Q.front ;
s=p->data;//队头存的数据
if(Q.front==Q.rear){
Q.front=Q.rear=NULL;
}
else{
Q.front =p->next;
}
free(p);
return s;
}
//取队头元素
void GetHead_Sq(LinkQueue Q,CSTree &p){
if(QueueEmpty(Q)){
exit(0);
}
p=Q.front->data ;
}
//初始化树
void InitTree_CST(CSTree &T){
}
//构造树
void CreateTree_CST(CSTree &T){
T=NULL;
LinkQueue Q;
InitQueue_Sq(Q);
ElemType parent,child;
CSTree p,q,r=new CSNode;
for(cin>>parent>>child;child!=0;cin>>parent>>child){
p=(CSTree)malloc(sizeof(CSNode));
p->data=child;
p->firstchild =p->rightsib =NULL;
EnQueue_Sq(Q,p);//append p to Q
if(parent==-1){
T=p;//root node
}
else{
GetHead_Sq(Q,q);
while(q->data != parent){
DeQueue_Sq(Q,q);
GetHead_Sq(Q,q);
}
if(!(q->firstchild )){
q->firstchild =p;
r=p;
}
else{
r->rightsib =p;
r=p;
}
}
}
}
//pre-order output
void PreOrderTraverse_CST(CSTree &T){
if(T){
cout<data<<" ";
PreOrderTraverse_CST(T->firstchild );
PreOrderTraverse_CST(T->rightsib );
}
}
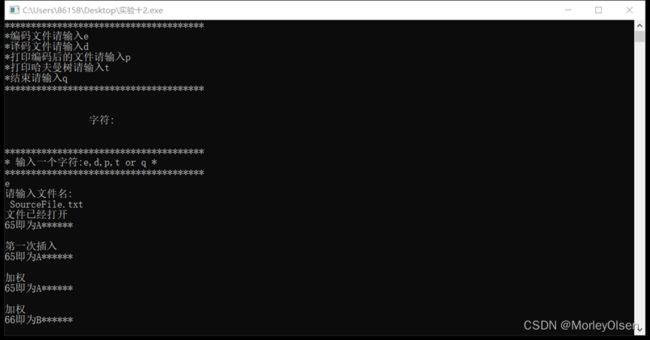
//mid-order output
void MidOrderTraverse_CST(CSTree &T){
if(T){
MidOrderTraverse_CST(T->firstchild );
cout<data<<" ";
MidOrderTraverse_CST(T->rightsib );
}
}
//layer-order output
void FloorTraverse_CST(CSTree &T){
LinkQueue Q;
InitQueue_Sq(Q);
if(T){
cout<data <<" ";
EnQueue_Sq(Q,T);//根结点排队
while(!QueueEmpty(Q)){
CSTree e,p;
e=(CSTree)malloc(sizeof(CSNode));
p=(CSTree)malloc(sizeof(CSNode));
DeQueue_Sq(Q,e);
p=e->firstchild ;
while(p){
cout<data<<" ";
EnQueue_Sq(Q,p);
p=p->rightsib ;
}
}
}
}
//销毁CST
void DestroyTree_CST(CSTree &T){
if(T){
DestroyTree_CST(T->firstchild );
DestroyTree_CST(T->rightsib );
free(T);
T=NULL;
}
}
//主函数
int main(){
CSTree T;
InitTree_CST(T);
cout<<"Input tree:"< 题目2
测试用例及运行结果:
测试用例1:AAABBC
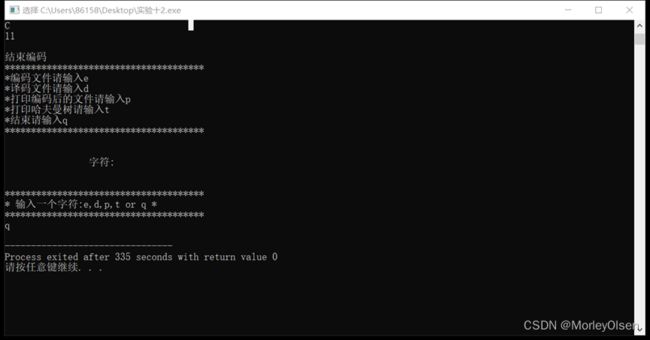
运行结果截图:
SourceFile.txt内容:
Code.txt内容:
ResultFile.txt内容:
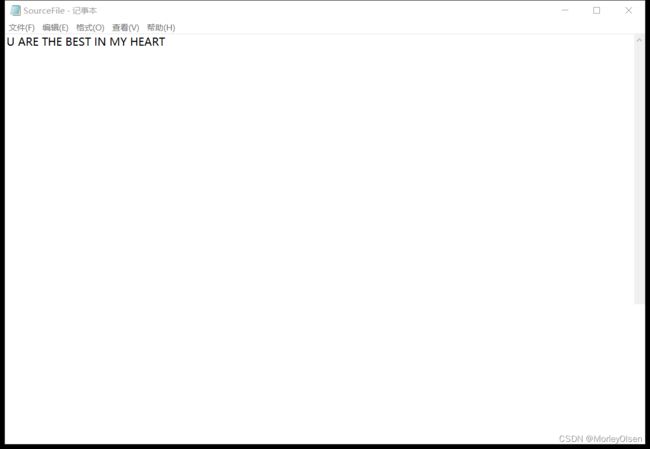
测试用例2:U ARE THE BEST IN MY HEART
运行结果截图:
SourceFile.txt内容:
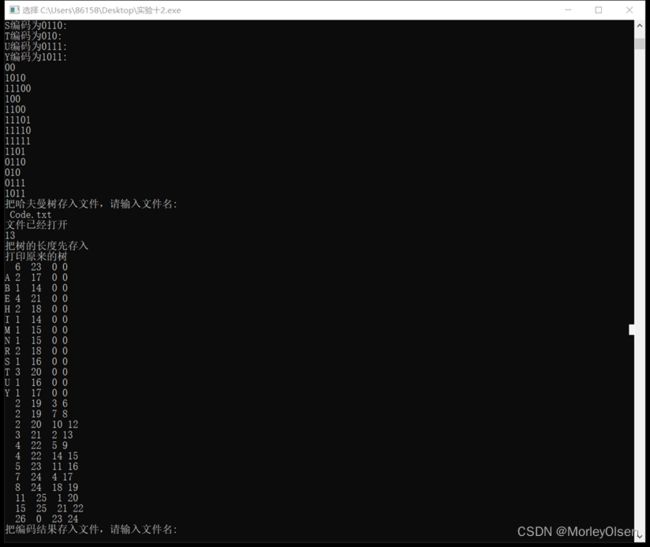
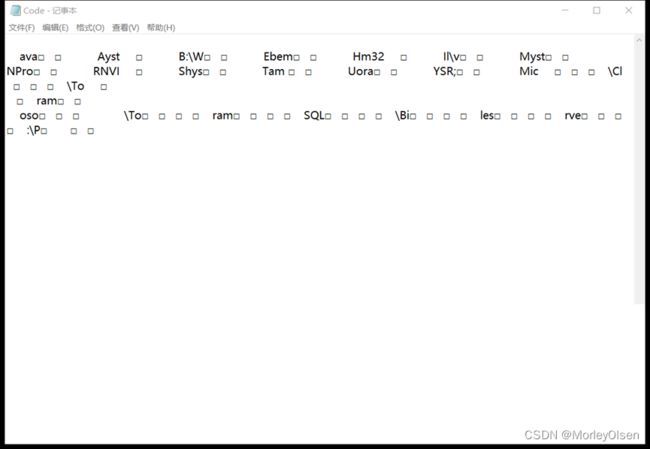
Code.txt内容:
ResultFile.txt内容:
运行过程:
读取SourceFile.txt文件->统计各个字符出现的频数->基于频数构建Huffman树->基于Huffman树建立Huffman表,即Code.txt文件->基于Huffman表对SourceFile.txt文件进行编码,结果为ResultFile.txt文件。
主要通过终端提示的字母信息进行相应操作。
实验代码:
#include
#include
#include
#include
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef struct HTNode
{
char leaf;
unsigned int weight;
unsigned int parent, lchild, rchild;
}HTNode, *HuffmanTree;
typedef char **HuffmanCode; //动态分配数组存储哈夫曼编码表
typedef struct Node
{
char leaf;
unsigned int weight;
struct Node * next;
}LeafNode, *LeafLink;
typedef struct
{
LeafLink head;
unsigned len;
}LeafLinkList;
int min1(HuffmanTree t, int i)
{ /* 函数void select()调用 */
int j, flag;
unsigned int k = UINT_MAX; /* 取k为不小于可能的值 */
for (j = 1; j <= i; j++)
if (t[j].weight*s2)
{
j = *s1;
*s1 = *s2;
*s2 = j;
}
}
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, LeafLinkList L)
{ /* w存放n个字符的权值(权值均需大于0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HC*/
int m, i, s1, s2, start;
int n = L.len;
unsigned c, f;
LeafLink ptr;
HuffmanTree p;
char *cd;
if (n <= 1)
return;
m = 2 * n - 1;
printf("表长为%d\t哈夫曼树含节点数为%d\n", n, m);
HT = (HuffmanTree)malloc((m + 1)*sizeof(HTNode)); /* 0号单元未用 */
ptr = L.head->next;
for (p = HT + 1, i = 1; i <= n; ++i, ++p, ptr = ptr->next)
{
(*p).leaf = ptr->leaf;
printf("%d\t", (*p).leaf);
(*p).weight = ptr->weight;
printf("%d\n", (*p).weight);
(*p).parent = 0;
(*p).lchild = 0;
(*p).rchild = 0;
}
for (; i <= m; ++i, ++p)
{
(*p).parent = 0;
(*p).leaf = 0;
}
for (i = n + 1; i <= m; ++i) /* 建哈夫曼树 */
{ /* 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2 */
select(HT, i - 1, &s1, &s2);
HT[s1].parent = HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
/* 从叶子到根逆向求每个字符的哈夫曼编码 */
HC = (HuffmanCode)malloc((n + 1)*sizeof(char*));
/* 分配n个字符编码的头指针向量([0]不用) */
cd = (char*)malloc(n*sizeof(char)); /* 分配求编码的工作空间 */
cd[n - 1] = '\0'; /* 编码结束符 */
for (i = 1; i <= n; i++)
{ /* 逐个字符求哈夫曼编码 */
start = n - 1; /* 编码结束符位置 */
for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
/* 从叶子到根逆向求编码 */
if (HT[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
HC[i] = (char*)malloc((n - start)*sizeof(char));
/* 为第i个字符编码分配空间 */
strcpy(HC[i], &cd[start]); /* 从cd复制编码(串)到HC */
}
free(cd); /* 释放工作空间 */
for (i = 1; i <= n; i++)
{
printf("%c编码为%s:\n", HT[i].leaf, HC[i]);
}
}
void InitLeafList(LeafLinkList &L)
{
L.head = (LeafLink)malloc(sizeof(LeafLink));
L.head->next = NULL;
L.len = 0;
}
void PrintList(LeafLinkList L)
{
LeafLink p;
p = L.head->next;
printf("打印链表\n");
printf("表长为%d\n", L.len);
while (p != NULL)
{
printf("%c or %d,%u\t", p->leaf, p->leaf, p->weight);
printf("打印一个节点\n");
p = p->next;
}
printf("打印结束\n");
printf("\n");
}
void EnLeafList(LeafLinkList &L, char ch)
{
LeafLink p, pre, temp;
int flag = 0;
pre = p = L.head;
printf("%d即为%c******\n\n", ch, ch);
if (p->next == NULL) //p->next=NULL则为第一次插入操作
{
printf("第一次插入\n");
temp = (LeafLink)malloc(sizeof(LeafNode));
temp->leaf = ch;
temp->weight = 1;
temp->next = NULL;
p->next = temp;
L.len++;
}
else
{
p = p->next;
while (p != NULL)
{
if (ch == p->leaf)
{
p->weight++;
printf("加权\n");
p = NULL;
flag = 1;
} //权重加一
else if (chleaf) //插入
{
printf("插入A\n");
temp = (LeafLink)malloc(sizeof(LeafNode));
temp->leaf = ch;
temp->weight = 1;
temp->next = p;
pre->next = temp;
L.len++;
flag = 1;
p = NULL;
}
else //继续寻找插入点
{
pre = p;
p = p->next;
}
}
if (p == NULL&&flag != 1) //若p=NULL则插到链尾
{
printf("插入B\n");
temp = (LeafLink)malloc(sizeof(LeafNode));
temp->leaf = ch;
temp->weight = 1;
temp->next = NULL;
pre->next = temp;
L.len++;
}
}
}
void EnCoding()
{
FILE *fp, *fr, *fc;
HuffmanTree HT;
HuffmanCode HC;
int i, n;
LeafLinkList L;
InitLeafList(L);
char filename[15];
char ch;
printf("请输入文件名:\n ");
scanf("%s", filename);
if (!(fp = fopen(filename, "r")))
{
printf("打开文件失败,请输入正确的文件名!! ");
exit(0);
}
ch = getchar(); //接收执行scanf语句时最后输入的回车符
printf("文件已经打开\n");
while (!feof(fp))
{
ch = fgetc(fp);
if (ch == -1)
{
printf("结束统计\n");
}
else
{
EnLeafList(L, ch);
}
}
PrintList(L);
HuffmanCoding(HT, HC, L);
n = L.len;
for (i = 1; i <= n; i++)
{
puts(HC[i]);
}
char TreeName[15];
printf("把哈夫曼树存入文件,请输入文件名:\n ");
scanf("%s", TreeName);
if (!(fr = fopen(TreeName, "wb")))
{
printf("打开文件失败,请输入正确的文件名!! ");
exit(0);
}
ch = getchar(); //接收执行scanf语句时最后输入的回车符
printf("文件已经打开\n");
//把哈夫曼树存入文件
printf("%d\n", n);
printf("把树的长度先存入\n");
_putw(n, fr); //把树的长度先存入
for (i = 1; i <= 2 * n - 1; i++)
if (fwrite(&HT[i], sizeof(struct HTNode), 1, fr) != 1)
printf("文件写入出错\n");
fclose(fr);
printf("打印原来的树\n");
for (i = 1; i <= 2 * n - 1; i++)
printf("%c %u %u %u %u\n", HT[i].leaf, HT[i].weight, HT[i].parent, HT[i].lchild, HT[i].rchild);
fclose(fr);
printf("把编码结果存入文件,请输入文件名:\n ");
char CodeFileName[15];
scanf("%s", CodeFileName);
if (!(fc = fopen(CodeFileName, "wb")))
{
printf("打开文件失败,请输入正确的文件名!! ");
exit(0);
}
ch = getchar(); //接收执行scanf语句时最后输入的回车符
printf("待编码的文件位置指针重新指向开始位置\n");
printf("对待编码文件进行编码,编码同步显示,并将结果存入指定的文件\n");
rewind(fp);
while (!feof(fp))
{
ch = fgetc(fp);
printf("%c\n", ch);
if (ch == -1)
{
printf("结束编码\n");
}
else
{
for (int tap = 0, i = 1; tap == 0 && i <= n;) //查找,该叶子对应的编码串
{
if (ch == HT[i].leaf) //找到,打印出对应的编码,并存入文件
{
printf("%s\n", HC[i]);
fputs(HC[i], fc); //将编码字符串存入文件
tap = 1;
}
else
{
i++;
}
}
}
}
fclose(fp); //关闭文件
fclose(fc); //关闭文件
}
int decode(FILE *fc, HuffmanTree HT, int n)
{
while (!feof(fc))
{
char ch = fgetc(fc);
if (ch == '0')
{
n = HT[n].lchild;
if (HT[n].leaf != 0)
{
printf("%c", HT[n].leaf);
return OK;
}
else
{
decode(fc, HT, n);
return OK;
}
}
else if (ch == '1')
{
n = HT[n].rchild;
if (HT[n].leaf != 0)
{
printf("%c", HT[n].leaf);
return OK;
}
else
{
decode(fc, HT, n);
return OK;
}
}
else return OK;
}
return ERROR;
}
//解码文件
void Decoding()
{
FILE *fc, *fr;
char CodeFileName[15], ch, TreeName[15];
int i;
printf("解码文件,请输入文件名(如*.dat):\n ");
scanf("%s", CodeFileName);
if (!(fc = fopen(CodeFileName, "r")))
{
printf("打开文件失败,请输入正确的文件名!! ");
exit(0);
}
ch = getchar(); //接收执行scanf语句时最后输入的回车符
printf("存放编码结果文件已经打开\n");
//读入哈夫曼树
HuffmanTree HT;
printf("取出对应的哈夫曼树文件,请输入文件名,\n");
scanf("%s", TreeName);
if (!(fr = fopen(TreeName, "rb"))) //打开存放哈夫曼树的文件
{
printf("打开文件失败,请输入正确的文件名!! ");
exit(0);
}
int n = _getw(fr); //将叶子数目取出
printf("叶子数目%d\n", n);
HT = (HuffmanTree)malloc((2 * n)*sizeof(HTNode)); /* 然后分配空间,0号单元未用 */
for (i = 1; i <= 2 * n - 1; i++)
if (fread(&HT[i], sizeof(struct HTNode), 1, fr) != 1)
printf("文件读出出错\n");
int length = 2 * n - 1; //总长度
printf("总结点数目为:%d\n", n);
printf("该文件译码后得到的源文件为:\n");
printf("**************************************\n");
while (!feof(fc))
{
decode(fc, HT, length);
}
printf("**************************************\n");
printf("\n\n");
}
int PreOrderPrint(HuffmanTree HT, int n, int count)
{
if (HT[n].lchild)
{
for (int i = 0; i