考研数据结构手记(3)-栈和队列
第三章 栈和队列
-
- 3.1 栈
-
- 3.1.1 栈的逻辑结构
-
- 习题1.1
- 3.1.2 栈的存储结构
-
- 3.1.2.1 顺序栈
- 3.1.2.2 链栈
- 习题1.2
- 3.1.3 栈的应用
-
- 3.1.3.1 括号匹配问题
- 3.1.3.2 表达式求值问题
-
- 中缀转后缀的手算方法
- 后缀表达式的手算方法
- 用栈实现后缀表达式的计算
- 用栈实现前缀表达式的计算:
- 中缀表达式转后缀表达式(机算)
- 用栈实现中缀表达式的计算:
- 3.1.3.3 栈的递归问题的应用
- 3.2 队列
-
- 3.2.1 队列的逻辑结构
- 3.2.2 队列的存储结构
-
- 3.2.2.1 顺序队列
- 3.2.2.2 链队
- 3.2.3 双端队列
- 3.2.4 队列的应用-树的层次遍历
- 3.3 输出序列问题
-
- 3.3.1 卡特兰数
3.1 栈
3.1.1 栈的逻辑结构
栈是一种只能在一端进行插入或删除操作的线性表。
栈:先进后出
习题1.1
已知程序如下:
int S(int n)
{
return (n<=0)?0:S(n-l)+n;
}
void main()
{
std::cout<<S(1);
}
程序运行时使用栈来保存调用过程的信息,自栈底到栈顶保存的信息依次对应的是main()→S(1)→S(0).
3.1.2 栈的存储结构
3.1.2.1 顺序栈
int stack[MAXSIZE];
int top = -1;
##定义栈的基本要素
stack[++top] = 1
stack[++top] = 2
stack[++top] = 3
stack[++top] = 4
##向栈中添加元素
x = stack[top--];
##元素出栈
栈中的元素编号是0~top,其他元素不属于栈中元素。
top == -1 ##栈空
top == MAXSIZE-1 ##栈满
3.1.2.2 链栈
## 链栈入栈操作
LNode *head = (LNode*)malloc(sizeof(LNode));
head->next = NULL;
top = (LNode*)malloc(sizeof(LNode));
top->next = NULL;
top->data = 'A';
top->next = head->next;
head->next = top;
## 链栈出栈操作
x = top->data;
head->next = top ->next;
free(x);
top = head->next;
## 栈空判断
head->next = NULL;
## 栈满判断
默认链栈不会栈满,可以时刻添加存储空间。
习题1.2
1.和顺序栈相比,链栈有一个比较明显的优势,即(A).
A.通常不会出现栈满的情况
B.通常不会出现栈空的情况
C.插入操作更容易实现
D.删除操作更容易实现
2.向一个栈顶指针为top的链栈(不带头结点)中插入一个x结点,则执行(C)
A. top->next=x
B.x->next=top->next; top->next=x
C. x->next=top; top=x
D.x->next=top,top-top->next
3.设栈的初始状态为空,当字符序列“n1_ ”作为栈的输入时,输出长度为3,且可用做C语言标识符的序列有( C)个.
A. 4
B. 5
C.3
D. 6
注解:
标识符的第一个字符必须是大小写英文字母或下画线,不能是数字。符合规定的标识符有n1_ ,n_1,_1n , _n1 四种形式。
"_n1"这种情况不可能出现,故选C.
3.1.3 栈的应用
3.1.3.1 括号匹配问题
{ ( ( ) ) [ ]}
用栈实现括号匹配:
依次扫描所有字符,遇到左括号入栈,遇到右括号则弹出栈顶元素检查是否匹配。
匹配失败情况:
①左括号单身②右括号单身③左右括号不匹配
3.1.3.2 表达式求值问题
中缀转后缀的手算方法
①确定中缀表达式中各个运算符的运算顺序
②选择下一个运算符,按照「左操作数右操作数运算符」的方式组合成一个新的操作数
③如果还有运算符没被处理,就继续②
"左优先"原则:只要左边的运算符能先计算,就优先算左边的,可以保证计算顺序的唯一性。
后缀表达式的手算方法
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算,
合体为一个操作数
注意:两个操作数的左右顺序
用栈实现后缀表达式的计算
①从左往右扫描下一个元素,直到处理完所有元素
②若扫描到操作数则压入栈,并回到①;否则执行③
③若扫描到运算符,则弹出两个栈项元素,执行相应运算,运算结果压回栈顶,回到①
用栈实现前缀表达式的计算:
①从右往左扫描下一个元素,直到处理完所有元素
②若扫描到操作数则压入栈,并回到①;否则执行③
③若扫描到运算符,则弹出两个栈项元素,执行相应运算,运算结果压回栈顶,回到①
按"左优先"原则确定运算符的运算次序,先弹出的元素是"右操作数"
按"右优先"原则确定运算符的运算次序,先弹出的元素是“左操作数"
中缀表达式转后缀表达式(机算)
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
①遇到操作数。直接加入后缀表达式。
②遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
③遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把当前运算符入栈。
用栈实现中缀表达式的计算:
初始化两个栈,操作数栈和运算符栈 若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)
3.1.3.3 栈的递归问题的应用
函数调用的特点:最后被调用的函数最先执行结束(LIFO)函数调用时,需要用一个栈存储:
①调用返回地址 ②实参 ③局部变量
递归调用时,函数调用栈可称为“递归工作栈”每进入一层递归,就将递归调用所需信息压入栈顶每退出一层递归,就从栈顶弹出相应信息。
3.2 队列
3.2.1 队列的逻辑结构
队列是一种插入元素只能在一端进行,删除元素只能在另一端进行的线性表。队列的逻辑结构属于线性表,只不过在操作上加了一些约束。可以插入元素的一端叫队尾(Rear),可以删除元素的—端叫队头(Front)。
队列:先进先出
3.2.2 队列的存储结构
3.2.2.1 顺序队列
## 初始化队列
int queue [maxSize];
int front = 0,rear = 0;
## 元素入队列
queue[++rear]=X;
## 元素出队列
X = queue [++front] ;
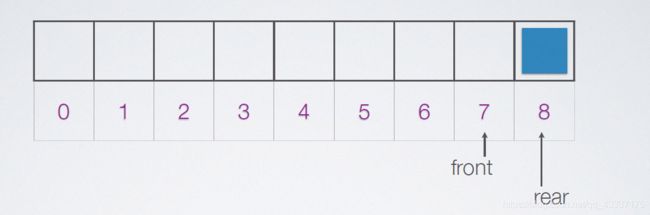
但是当把一个队列进行操作后变成上面这样的情况时,队列有空间但却没有办法让元素入队,所以发生了“假溢出”。
所以就把队列改良成环形:

入队:
rear = (rear+1)%maxSize;
queue[rear] = X;
出队∶
front =(front+1)%maxSize;
X = queue[front];
队空:
front == rear;
队满:
front == (rear +1)%maxSize;
3.2.2.2 链队
typedef struct{
LNode* front;
LNode* rear;
}queue;
3.2.3 双端队列
双端队列:允许从两端插入、两端删除的队列
输入受限的双端队列:
允许从两端删除、从一端插入的队列
输出受限的双端队列:
允许从两端插入、从一端删除的队列
3.2.4 队列的应用-树的层次遍历
3.3 输出序列问题
设栈S和队列Q的初始状态均为空,元素a、b、c、d、e、f、g依次进入栈S。若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是b、d、c、f、e、a、g,则栈S的容量至少是(3)
就是根据先进后出的顺序进行判断。
若元素a、b、c、d、e、f依次进栈,允许进栈、出栈操作交替进行,但不允许连续三次进行出栈操作,则不可能得到的出栈序列是(a、f、e、d、c、b)
入栈顺序与出栈顺序不符。
元素a,b,c,d,e依次进入初始为空的栈中,若元素进栈后可停留、可出栈,直到所有元素都出栈,则在所有可能的出栈序列中,以元素d开头的序列个数是(4)个
decba
dceba
dcbea
dcbae
3.3.1 卡特兰数
Cn= (2n)! / [(n+1)! n!]
n个数按照某种顺序入栈,并且可在任意时刻出栈,不同出栈序列的个数为Cn。




