基于符号抽象的程序分析

原文来自微信公众号“编程语言Lab”：基于符号抽象的程序分析
搜索关注“编程语言Lab”公众号（HW-PLLab）获取更多技术内容！
欢迎加入 编程语言社区 SIG-程序分析 参与交流讨论（加入方式：添加小助手微信 pl_lab_001，备注“加入SIG-程序分析”）。

分享嘉宾 | 姚培森@rainoftime

回顾整理 | 纪妙

作者介绍

姚培森 @rainoftime，浙江大学网络空间安全学院特聘研究员，研究领域为程序分析与验证、自动推理。

个人主页：https://rainoftime.github.io/

视频回顾

SIG-程序分析技术沙龙回顾｜基于符号抽象的程序分析

前言

软件已经无处不在，软件质量问题也越来越普遍，其造成的系统崩溃、安全漏洞等可能带来经济上的损失，甚至威胁我们的生命。程序分析是保障软件质量的基础技术和重要手段，已被广泛应用于提高软件的可靠性、安全性、性能等多个维度的质量。

今天，我们探讨一类特殊的程序分析方法，基于符号抽象的程序分析。首先我会简单回顾一下 抽象解释 —— 静态分析的核心理论。抽象解释的核心问题之一是，计算程序状态在给定抽象域内的最佳抽象。针对这个问题，我会介绍符号抽象框架以及几个和符号抽象有关的其他话题。

抽象解释

抽象解释是静态分析的核心理论 ¹，其关键想法是对程序的可达状态做一个上近似。

如下图，假设左边的黄色椭圆代表程序的可达状态 Reachable States，右边的黄色椭圆代表有缺陷的状态 Bad States。我们想验证这个程序是否有缺陷，即 Reachable States 是否可能和 Bad States 相交。

静态分析可以对程序的可达状态做推理，比如算出一个红色区域。最终红色区域可以完全覆盖左边的黄色区域，因此我们得到了一个上近似。而且我们看到左边红色区域和 Bad States 并不相交，因此我们成功地验证了这个程序是安全的。

1.1 抽象解释的应用

过去 20 多年来，抽象解释在工业界得到了很多应用，以下三个可能是比较有代表性的。

第一个是 Astrée，基于数值域抽象解释，已经成功用于验证航空航天等安全攸关场景的软件。

第二个是 TVLA，主要做形态分析，比如验证垃圾回收算法是否真的回收了内存垃圾。TVLA 把形态分析这个概念给发扬光大了，启发了很多后续工作，比如基于分离逻辑的形态分析。

第三个是 CodeSurfer/x86，它提出的 Value Set Analysis (VSA) 已经成为了二进制静态分析框架的标配。

此外，抽象解释在学术领域也获得多个荣誉，包括 2013 年 SIGPLAN 的程序语言成就奖， 2018 年的约翰·冯诺依曼奖等。

左图为 2013 年 SIGPLAN 程序语言成就奖，右图为 2018 年约翰·冯诺依曼奖

1.2 抽象域及其要素

抽象解释会通过抽象域来对程序的状态做数学近似，比如数值域、堆域、字符串域等。其中，数值域可以用来捕捉程序的数值信息，用于查找不同的程序缺陷，包括除零错误、整数溢出等。


由于抽象解释是对程序的可达状态做上近似，它往往伴随着一些精度问题。比如我们再次看这个图，右边的黄色区 Bad States 和红色区域 (静态分析的结果) 是相交的，但事实上 Bad States 和左边的黄色区域 Reachable States 并不相交，因此我们的静态分析存在误报。

1.3 最佳抽象

给定一个抽象域比如区间域，怎么计算程序在该抽象域上的、最精确的上近似呢？事实上，这也是抽象解释理论的一个核心问题：给定一个具体迁移函数 $F$ 以及抽象域 $A$，如何得到 $F$ 在 $A$ 上的最佳抽象 $F^{\#}$ （最精确的抽象迁移函数）？

抽象解释理论对 $F^{\#}$ 有一个声明式的定义，但是这个定义是“非构造性”的。通常我们没有自动化的算法，去应用最佳抽象迁移函数 $F^{\#}$，或者去得到 $F^{\#}$ 的一个表示。

最佳抽象的形式化定义：

符号抽象框架

为了解决以上问题，研究人员提出了符号抽象框架。

2.1 框架定义和实例

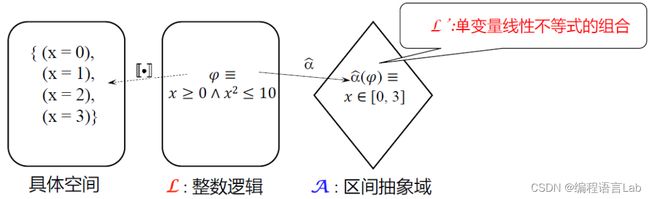
假设我们用逻辑约束 $\phi$ 来编码一个程序的具体状态，并且把抽象域 $A$ 看作一个比较受限的逻辑片段（比如 “区间逻辑”）。符号抽象的目标就是找到约束 $\phi$ 在抽象域 $A$ 上的、最精确的上近似 ²。

我们也可以从逻辑的角度来理解 ³。给定一个约束 $\phi$ 和一个逻辑片段 $L’$（对应于抽象域）, 找到约束 $\phi$ 在 $L’$ 中的最强逻辑后承（strongest logical consequence）。

下面是一个具体的例子:

考虑约束 $\phi \equiv x\ge 0\wedge x^2\le 10$，其中 $x$ 是整数变量。这个约束有四个可行解 $(x=0),(x=1),(x=2),(x=3)$。可以一眼看出来，约束 $\phi$ 在区间域的最佳近似是 $[0,3]$。但是，在一般情况下，我们应如何计算出一个约束的最佳区间近似呢？这就是符号抽象需要解决的问题。

2.2 框架意义和应用

通常，为了实现一个静态分析器，我们需要建模不同的程序指令 (比如加减乘除)，为其设计不同的抽象迁移函数、并将这些迁移函数组合起来。而使用符号抽象框架后，我们就可以用一个约束来精确编码一整块代码，并且自动得到对于该代码的最精确近似。

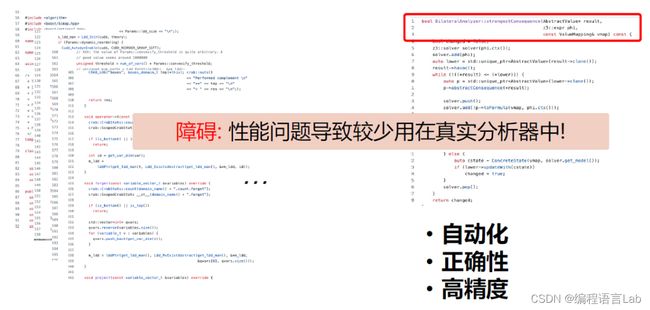
然而，由于符号抽象的性能问题，目前在真实的静态分析器中很少得到应用。当前的少量应用主要包括两块。

一是上层源代码的验证分析，包括数值属性、堆属性等的验证。对于数值验证，国防科大的陈立前教授就有相关工作 ⁴。目前这些工作主要面向一些相对小规模的程序验证。

其次是二进制分析，比如做控制流恢复 control flow recovery 等。在欧洲有几个团队一直有做相关的工作，GrammaTech 甚至已经将符号抽象用到二进制分析产品中。

但即便有工业级应用，符号抽象在形式化、编程语言、甚至抽象解释社区也都还不够普及。

延伸思考

下面分享一些引申思考。回到符号抽象的定义：$L$ 是表达力丰富的逻辑，抽象域 $A$ 对应于 $L$ 一个子集 $L’$。 给定 $\Phi \in L$，找到它在 $L’$ 的最强逻辑后承。

其实计算机科学中的很多问题都跟这个问题相关，下面我们举几个例子。

第一个是谓词抽象 predicate abstraction ⁵，它可以看作符号抽象的一个特殊实例。假设我们有一些谓词集合 $S=x>3,\dots ,x+y<10$，谓词抽象的抽象域 $L’$ 就是 $S$ 中命题的任意布尔组合，比如 $x>3orx+y<10$。在用于程序验证时，结合一些不动点迭代方式，我们还能算出 $L’$ 能表达的最强循环不变式。

第二个是量词消去 quantifier elimination。给定 $\Phi \in L$，假设抽象域 $L’$ 是只使用特定约束变量集合 $S\subseteq Vars(\Phi )$ 的约束。那么，存在量词消去 existential quantifier elimination 的目标就是计算 $\Phi$ 在 $L’$ 中的最强逻辑后承。

第三个是人工智能里面的 Forgetting 问题 ⁶，和量词消去问题类似。这是港科大 Fangzhen Lin 教授发明的概念，在逻辑 AI 领域很有名。

第四个是 线性规划 问题，它也可以看作符号抽象问题的一个实例。$L$ 即线性约束集合，$L^{\prime }:f(X)⩽c$ (其中，$f$ 是线性目标函数)。

个人认为符号抽象问题有超越静态分析、编程语言，甚至超越计算机科学领域的意义，具有深远的理论蕴含。而且针对相关问题的算法也有一些共通性，比如基于模型的泛化等。

总结与展望

最后，我们一起从 程序合成 的视角来理解符号抽象 (程序合成是指如何自动从规约中生成程序)。那么，回顾今天的主题，我们的规约是什么？我们应如何从这个规约中生成静态分析器呢？

参考文献

---

1. Patrick Cousot, and Radhia Cousot. “Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints.” In Proceedings of the 4th ACM SIGACT-SIGPLAN symposium on Principles of programming languages, pp. 238-252. 1977. ↩︎

2. Thomas Reps, Mooly Sagiv, and Greta Yorsh. “Symbolic implementation of the best transformer.” In International Workshop on Verification, Model Checking, and Abstract Interpretation, pp. 252-266. Springer, Berlin, Heidelberg, 2004. ↩︎

3. Thomas Reps, and Aditya Thakur. “Automating abstract interpretation.” In International Conference on Verification, Model Checking, and Abstract Interpretation, pp. 3-40. Springer, Berlin, Heidelberg, 2016. ↩︎

4. Jiahong Jiang, Liqian Chen, Xueguang Wu, and Ji Wang. “Block-wise abstract interpretation by combining abstract domains with smt.” In International Conference on Verification, Model Checking, and Abstract Interpretation, pp. 310-329. Springer, Cham, 2017. ↩︎

5. Susanne Graf, and Hassen Saidi. “Construction of abstract state graphs with PVS.” In International Conference on Computer Aided Verification, pp. 72-83. Springer, Berlin, Heidelberg, 1997. ↩︎

6. Fangzhen Lin, and Ray Reiter. “Forget it.” In Working Notes of AAAI Fall Symposium on Relevance, pp. 154-159. 1994. ↩︎