【深度学习】基于图形的机器学习:概述
一、说明
图神经网络(GNN)在数据科学和机器学习中越来越受到关注,但在专家圈之外仍然知之甚少。为了掌握这种令人兴奋的方法,我们必须从更广泛的图形机器学习(GML)领域开始。许多在线资源谈论GNN和GML,就好像它们是可互换的概念,或者好像GNN是一种灵丹妙药,使其他GML方法过时。事实并非如此。GML的主要目的之一是压缩大型稀疏图数据结构,以实现可行的预测和推理。GNN是实现这一目标的一种方法,也许是最先进的方法,但不是唯一的方法。理解这一点将有助于为本系列的后续部分奠定更好的基础,我们将更详细地介绍特定类型的GNN和相关GML方法。
在这篇文章中,我们将:
- 简要回顾一下图形数据结构
- 涵盖 GML 任务及其解决的问题类型
- 研究压缩的概念及其在驱动不同GML方法(包括GNN)方面的重要性
二、什么是图(graph)?
如果您正在阅读本文,您可能已经对图形数据结构有一些了解。如果没有,我建议阅读有关属性图的此资源或有关图形数据库概念的此资源。我将在这里做一个非常简短的回顾:
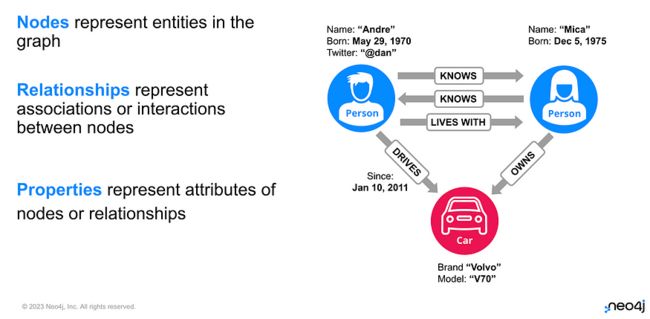
图由通过关系连接的节点组成。有几种不同的方法可以对图形数据进行建模。为简单起见,我将使用属性图模型,该模型有三个主要组件:
- 表示实体(有时称为顶点)的节点,
- 表示节点之间的关联或交互的关系(有时称为边或链接),以及
- 表示节点或关系的属性的属性。
图片来源:作者
三、什么是图机器学习(GML)?
图机器学习 (GML) 的核心是将机器学习应用于专门用于预测性和规范性任务的图形。GML 在供应链、欺诈检测、推荐、客户 360、药物发现等方面拥有各种用例。
理解GML的最佳方法之一是通过它可以完成的不同类型的ML任务。我在下面将其分解为有监督和无监督的学习。
3.1 受监督的 GML 任务
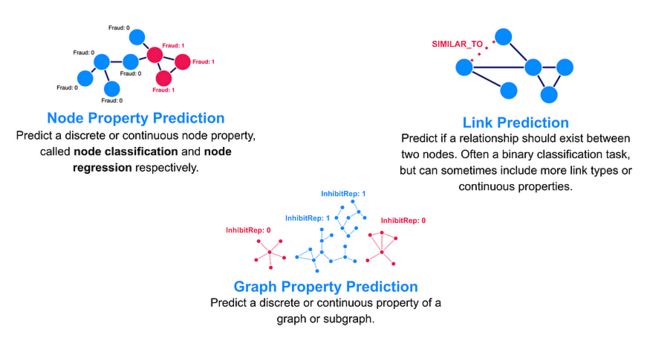
下图概述了监督学习中最常见的三个GML任务:
图片来源:作者
要进一步扩展:
- 节点属性预测: 预测离散或连续节点属性。人们可以将节点属性预测视为预测有关事物的形容词,例如金融服务平台上的帐户是否应归类为欺诈或如何对在线零售商店中的产品进行分类。
- 链路预测:预测两个节点之间是否存在关系,以及有关该关系的潜在一些属性。链接预测对于实体解析等应用程序很有帮助,在这些应用程序中,我们希望预测两个节点是否反映相同的底层实体;推荐系统,我们希望预测用户接下来想要购买或与之互动的内容;和生物信息学,用于预测蛋白质和药物相互作用等。对于每种情况,我们都关心预测实体之间的关联、相似性或潜在操作或交互。
- 图形属性预测:预测图或子图的离散或连续属性。图形属性预测在您希望将每个实体建模为单个图形以进行预测的域中非常有用,而不是将实体建模为表示完整数据集的较大图形中的节点。用例包括材料科学、生物信息学和药物发现,其中单个图形可以表示您想要进行预测的分子或蛋白质。
3.2 无监督的 GML 任务
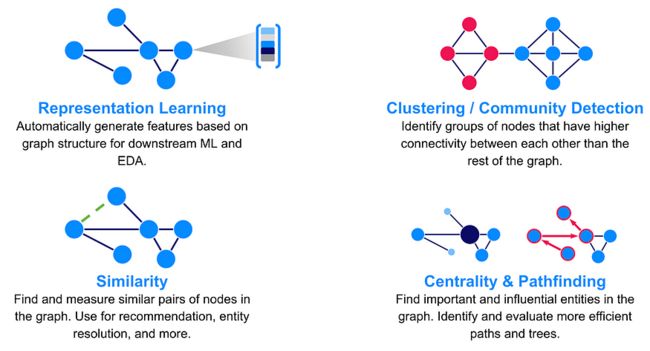
以下是无监督学习最常见的四个GML任务:
图片来源:作者
进一步详细说明这些:
- 表征学习:在保持重要信号的同时降低维数是GML应用的核心主题。图表示学习通过从图结构生成低维特征来明确地做到这一点,通常用于下游探索性数据分析 (EDA) 和 ML。
- 社区检测(关系聚类):社区检测是一种聚类技术,用于识别图中密集互连的节点组。社区检测在异常检测、欺诈和调查分析、社交网络分析和生物学方面具有各种实际应用。
- 相似性: GML中的相似性是指在图中查找和测量相似的节点对。相似性适用于许多用例,包括推荐、实体解析以及异常和欺诈检测。常见的相似性技术包括节点相似性算法、拓扑链路预测和 K-最近内博尔 (KNN)。
- 中心性和寻路:我将它们组合在一起,因为它们往往与 ML 任务的关联较少,而与分析度量的关联更多。但是,它们在技术上仍然适合这里,因此为了完整起见,我将介绍它们。中心性在图形中查找重要或有影响力的节点。中心性在许多用例中无处不在,包括欺诈和异常检测、推荐、供应链、物流和基础设施问题。路径查找用于查找图形中成本最低的路径或评估路径的质量和可用性。寻路可以使许多处理物理系统的用例受益,例如物流、供应链、运输和基础设施。
四、压缩如何成为 GML 的关键
我看到了Matt Ranger的这篇有趣的博客文章,它很好地解释了这一点:GML最重要的目标之一,在很大程度上也是自然语言处理,是压缩大型稀疏数据结构,同时保持重要的预测和推理信号。
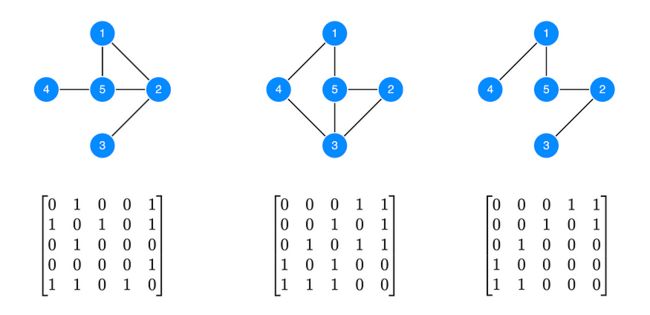
考虑一个由邻接矩阵表示的常规图形,一个方阵,其中每行和每列代表一个节点。如果关系从节点 A 到节点 B,则行 A 和列 B 交点处的单元格为 1;否则,为 0。下面是一些小的正则图及其邻接矩阵的插图。
图片来源:作者
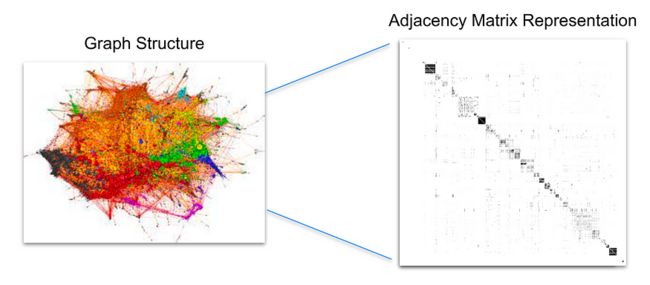
请注意,上述邻接矩阵中的许多单元格均为 0。如果将其缩放到大型图形,尤其是在实际应用中发现的图形,则零的比例会增加,邻接矩阵将变为大部分为零。
使用来自大型图形可视化工具和方法的推荐图视觉对象和来自Beck,Fabian等人的矩阵图像创建的 Last.fm 说明性示例。 通过多个层次结构的可视化比较来识别模块化模式
发生这种情况是因为随着这些图的增长,平均度中心性增长得更慢或根本不增长。在社交网络中,邓巴数等概念证明了这一点,邓巴数是对可以与之保持稳定社会关系的人数的认知限制。您也可以直观地了解其他类型的图表,例如金融交易图表或推荐系统的用户购买图表。随着这些图表的增长,一个人可以参与的潜在唯一交易或购买的数量增长速度远远快于他们这样做的能力。即,如果一个网站上有六种产品,一个用户购买其中的一半是可行的,但如果有数十万种,那就没有那么多了。结果,您最终会得到非常大且稀疏的数据结构。
如果你可以直接将这些稀疏数据结构用于机器学习,你就不需要GNN或任何GML——你只需将它们作为特征插入到传统的ML模型中。但是,这是不可能的。它不会扩展,甚至超过这个范围,它还会导致围绕收敛和估计的数学问题,从而使ML模型不明确且不可行。因此,GML 的基本关键是压缩这些数据结构;可以说,这是GML的全部意义所在。
五、如何完成压缩?— 图机器学习方法
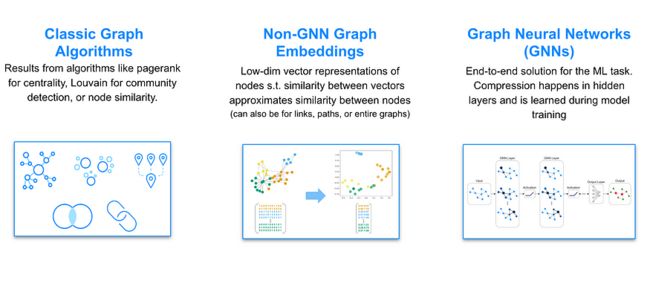
在最高级别,有三种GML方法可以实现这种压缩。
图片来源:作者
经典图形算法
经典的图形算法包括PageRank,Louvain和Dijkstra的最短路径。它们可以独立用于无监督的社区检测、相似性、中心性或寻路。经典算法的结果也可以用作传统下游模型的特征,例如线性和逻辑回归、随机森林或执行 GML 任务的神经网络。
经典的图算法往往很简单,易于上手,并且相对可解释和可解释。但是,与其他GML方法相比,它们可能需要更多的手动工作和主题专业知识(SME)。这使得经典的图算法成为实验和开发中的首选,以帮助了解什么在你的图上效果最好。对于更简单的问题,它们也可以在生产中做得很好,但更复杂的用例可能需要升级到另一种 GML 方法。
非GNN图嵌入
图嵌入是表征学习的一种形式。一些图嵌入技术利用GNN架构,而另一些则没有。后一组,即非GNN,是这种方法的重点。相反,这些嵌入技术依赖于矩阵分解/分解、随机投影、随机游走或散列函数架构。一些例子包括Node2vec(基于随机漫游),FastRP(随机投影和矩阵运算)和HashGNN(散列函数架构)。
图形嵌入涉及生成数字或二进制特征向量来表示节点、关系、路径或整个图形。其中最重要的是节点嵌入,是最基本和最常用的。基本思想是为每个节点生成一个向量,使得向量之间的相似性(例如点积)近似于图中节点之间的相似性。下面是一个小型Zachary空手道俱乐部网络的说明性示例。请注意如何将邻接矩阵压缩为每个节点的二维嵌入向量,以及这些向量如何聚类在一起以反映图形社区结构。大多数现实世界的嵌入将具有两个以上的维度(2 到 128 或更高)来表示具有数百万或数十亿个节点的更大的真实世界图,但基本直觉是相同的。
图片来源:作者
与上述相同的逻辑适用于关系、路径和整个图嵌入:嵌入向量中的相似性应近似于图结构中的相似性。这样可以在保持重要信号的同时完成压缩,使嵌入可用于各种下游 ML 任务。
与传统图形算法相比,非GNN嵌入可以从减少的手动工作量和所需的SME中受益。虽然非GNN嵌入通常需要超参数调优才能正确,但它们往往更容易在不同的图上自动化和泛化。此外,一些非GNN嵌入,如FastRP和HashGNN,可以很好地扩展到商品硬件上的大型图,因为它们不需要模型训练。与基于 GNN 的方法相比,这可能是一个巨大的好处。
但是,非GNN嵌入也有一些权衡。由于涉及更广义的数学运算,它们比经典图算法更不易于解释和解释。它们通常也是转导的,尽管Neo4j图数据科学的最新改进允许其中一些在某些应用程序中有效地进行归纳行为。我们将在本系列的后面更深入地介绍转导和感应设置;它与预测新的看不见的数据的能力有关,是GML的一个重要考虑点。
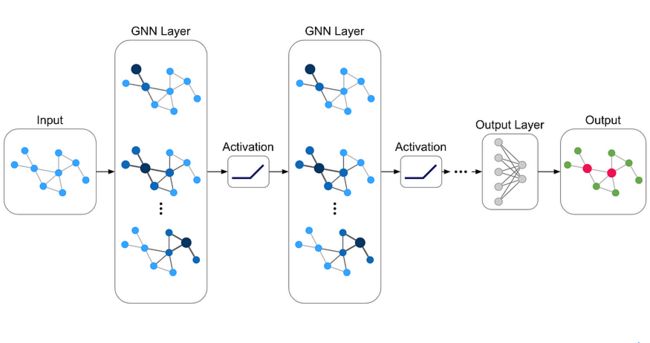
图神经网络 (GNN)
GNN 是一种神经网络模型,它将图数据作为输入,将其转换为中间嵌入,并将嵌入馈送到与预测任务对齐的最后一层。此预测任务可以是有监督的(节点属性预测、链接预测、图属性预测)或无监督的(聚类、相似性或只是用于表示学习的最终输出嵌入)。因此,与经典算法和非GNN嵌入不同,经典算法和非GNN嵌入将结果作为特征传递给下游ML模型,特别是对于监督任务,GNN是完全端到端的图形原生解决方案。
GNN 具有与完整的端到端解决方案相关的各种好处。值得注意的是,中间嵌入是在训练过程中学习的,理论上,它会自动从图中推断出最重要的信息。由于具有经过训练的模型,最新的GNN也是归纳的。
GNN也有一些弱点。这包括高复杂性、缩放困难以及低可解释性和可解释性。由于过度平滑和其他数学原理,GNN 也可能在深度方面受到限制。
我将在我的下一篇博客GNN:它们是什么以及它们为什么重要中更多地讨论GNN。同时,如果你想开始学习图机器学习,请查看Neo4j图数据科学。数据科学家和工程师可以在此处找到入门技术文档。
六、总结一下
这篇文章的最大收获:
- 图形机器学习 (GML) 是一个广泛的领域,具有许多用例应用程序,包含多个不同的监督和无监督 ML 任务
- GML的主要目的之一是压缩大型稀疏图结构,同时保持用于预测和推理的重要信号。
- GNN 是实现此压缩的多种 GML 方法之一。
扎克·布鲁门菲尔德