php image 平滑曲线,JavaScript折线转化为平滑曲线的一种方案
在前端的各种图表框架中,经常会有将一段折线平滑的需求,不仅能给用户带来一种柔和的感觉,还能美化界面,让折线看起来没那么生硬。这篇文章就来介绍一种折线平滑化的一种方案。
基础知识–三次贝塞尔曲线
在前端,能有用到曲线的地方,也就在绘图元素canvas中了。canvas提供了原生的两种绘制曲线的方法,二次贝塞尔曲线和三次贝塞尔曲线。本文介绍的这种方案便采用三次贝塞尔曲线来完成。
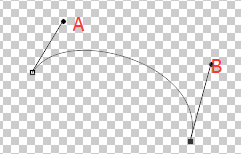
熟悉PhotoShop等绘图软件的朋友都知道,在PS中有一个工具叫钢笔工具,它是专门用来绘制曲线的。下面是一段用PS绘制出来的曲线
可以看到,这段曲线除了起点和终点之外,还有两个控制点A、B,更改他们的位置能相应的更改这段曲线的形状。
关于其中具体的计算方法及曲线的生成过程,可以参考文章:http://www.cnblogs.com/hnfxs/p/3148483.html
这里放一个文中生成曲线的gif图
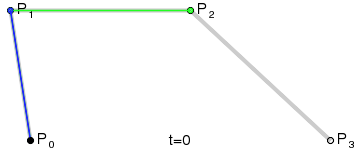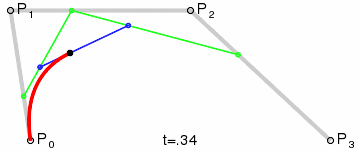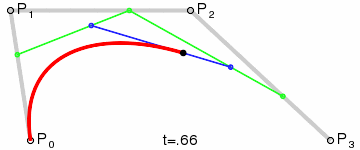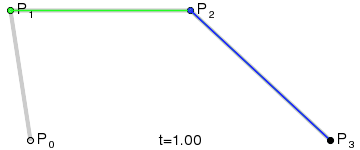
这个图中,P0为起点,P3为终点,P1、P2分别是曲线的两个控制点,红色线条是生成的曲线,其他的都是辅助线。
如上,其实不算是本文的重点内容,关于贝塞尔曲线,你只需记住以下几个重要特征:
1、一段三次贝塞尔曲线由四个点控制生成:起点、终点和两个控制点;
2、起点P0与控制点P1的连线与曲线相切,终点P3与控制点P2的连线也与曲线相切;
3、图中每条辅助线段都被一个点分为两段,且每条辅助线上两段的比例都是相同的。
折线平滑原理
在了解了三次贝塞尔曲线的原理之后,折线平滑的原理是很容易理解的。
在上面的gif图中,我们新增一个点P6,以及P3的另一个控制点P4,P6的控制点P5。
那么,从P0到P3,再从P3到P6,这之间的直线相连,也就构成了一段折线,我们的任务便是使P3至P6这段直线也曲线化。
并且为了保证两段曲线的连贯性,P3至P6这段曲线起点的切线必须与上一段曲线终点的切线共线。
有了以上这个分析,我们假设P4为P3的控制点,P5为P6的控制点,那么我们最终的任务便是寻找这两个控制点P4和P5。
所以任务最终化解为,只需要保证P2、P3、P4这三点之间的连线共线即可。
为了讨论的方便,在上图中,我们称
P0、P3、P6为折线的顶点;
P0也叫折线的起点,P6也叫折线的终点;
P1、P2、P4、P5都称为控制点;
可以看出,起点和终点只有一个控制点,其他顶点都有两个控制点。
有了如上的分析和假设,下面给出折线平滑化的一种方案:
1、任意顶点与控制点的连线始终平行于x轴;
2、控制点与顶点的距离,根据顶点的相邻顶点在x轴方向上的距离乘以某个系数来确定;
3、起点和终点的控制点为其本身;
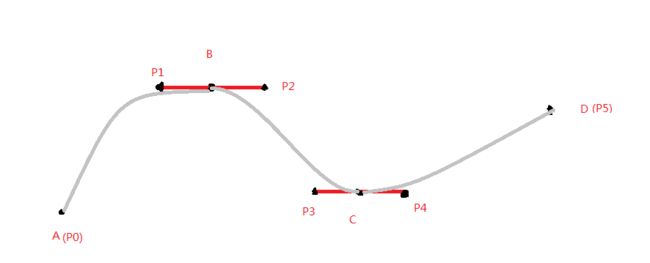
这个方案的大致意思就是下面这张图了
图中A、B、C、D为4个顶点,P0、P1、P2、P3、P4、P5为控制点,A为起点、D为终点。
方案强制控制点的连线平行于X轴,这样一来就保证了控制点与顶点的连线能够共线,再根据三次贝塞尔曲线的原理,就能将类似于上面这样的折线ABCD平滑化了。
方案的实现
看了这么多理论知识,我估计作为读者朋友的你早就腻了,脑子是不是不够用了啊?没关系,下面我就把我写好的代码放出来。
/**
* 绘制平滑的曲线
* @param pointList {Ycc.Math.Dot[]} 经过转换后的舞台绝对坐标点列表
*/
Ycc.UI.BrokenLine.prototype._smoothLineRender = function (pointList) {
// 获取生成曲线的两个控制点和两个顶点,N个顶点可以得到N-1条曲线
var list = getCurveList(pointList);
// 调用canvas三次贝塞尔方法bezierCurveTo逐一绘制
this.ctx.beginPath();
for(var i=0;i
this.ctx.moveTo(list[i].start.x,list[i].start.y);
this.ctx.bezierCurveTo(list[i].dot1.x,list[i].dot1.y,list[i].dot2.x,list[i].dot2.y,list[i].end.x,list[i].end.y);
}
this.ctx.stroke();
/**
* 获取曲线的绘制列表,N个顶点可以得到N-1条曲线
* @return {Array}
*/
function getCurveList(pointList) {
// 长度比例系数
var lenParam = 1/3;
// 存储曲线列表
var curveList = [];
// 第一段曲线控制点1为其本身
curveList.push({
start:pointList[0],
end:pointList[1],
dot1:pointList[0],
dot2:null
});
for(var i=1;i
var cur = pointList[i];
var next = pointList[i+1];
var pre = pointList[i-1];
// 上一段曲线的控制点2
var p1 = new Ycc.Math.Dot(cur.x-lenParam*(Math.abs(cur.x-pre.x)),cur.y);
// 当前曲线的控制点1
var p2 = new Ycc.Math.Dot(cur.x+lenParam*(Math.abs(cur.x-next.x)),cur.y);
// 上一段曲线的控制点2
curveList[i-1].dot2 = p1;
curveList.push({
start:cur,
end:next,
dot1:p2,
dot2:null
});
}
// 最后一段曲线的控制点2为其本身
curveList[curveList.length-1].dot2=pointList[pointList.length-1];
return curveList;
}
};
上面代码中的Ycc.UI是我框架的一个全局变量,不用理会。
重点关注函数getCurveList即可。看不懂的朋友多琢磨琢磨吧,明白了原理,代码实现很简单。
最后上一个示例链接:
结尾总结
最近工作忙,小站更新频率低,这篇文章年前起的头,现在才来完善,大伙见谅!
打赏作者
微信支付
支付宝