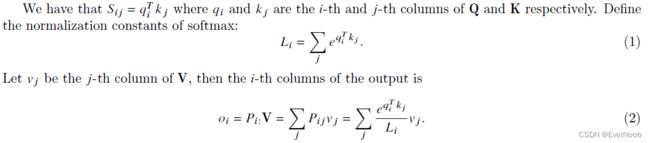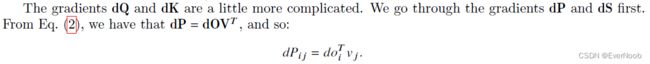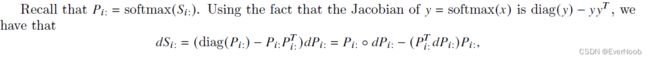FlashAttention

Sources

paper: https://arxiv.org/abs/2205.14135

an informal talk by the author Tri Dao: https://www.youtube.com/watch?v=FThvfkXWqtE

code repo: GitHub - HazyResearch/flash-attention: Fast and memory-efficient exact attention 

introduction to transformer: Transformer and Bert_EverNoob的博客-CSDN博客

Key Takeaways

Key features of FlashAttention (in the paper title): fast, memory-efficient, exact

Key algorithmic ideas

• tiling: avoid loading/unloading N*N matrices at once ==> one key here is how to break down softmax into linearly recoverable partials sums;
• recomputation: avoid saving intermediate results, compute them again during back-propagation instead.

The upshot: faster model training, better models with longer sequences (longer context for more accurate parsing).

Attention to FlashAttention

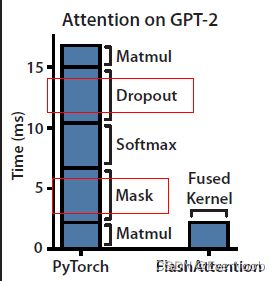
Regular Attention:

the heavy memory access is marked below:

a full version of the algorithm is:

the mask and dropout stages are not necessary, but they can be used to enhance training results; both of these perf. opt. steps introduce additional heavy memory costs. 

to reduce memory traffic, we want to:

1. compute softmax piecewise per tiling

2. skip saving intermediate results (S, P)

which is the most memory demanding being N*N

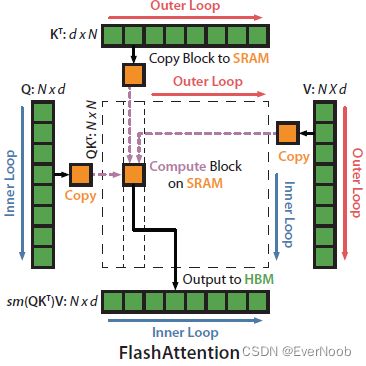
 We apply two established techniques (tiling, recomputation) to overcome the technical challenge of computing exact attention in sub-quadratic HBM accesses. We describe this in Algorithm 1. The main idea is that we split the inputs Q, K, V into blocks, load them from slow HBM to fast SRAM, then compute the attention output with respect to those blocks.

Tiling

By scaling the output of each block by the right normalization factor before adding them up, we get the correct result at the end.

 there is a mathematically equivalent parital sum:

and we only need to record max and partial exp. sum per block to break the interdependence among the blocks.

Recomputation

for backward pass:

the backward pass for standard attention is listed below, with the avoidable memory costs boxed out: 

notably for FlashAttention, we do not save P

how to compute the gradients with saved softmax normalization statistics is discussed below.

FlashAttention Forward and Backward Implmentation

Memory Efficient Forward Pass

Memory Efficient Backward Pass

==> the ":" denotes row-wise; the hollow dot denotes pointwise multiplication.

from here

The Jacobian matrix collects all first-order partial derivatives of a multivariate function that can be used for backpropagation. The Jacobian determinant is useful in changing between variables, where it acts as a scaling factor between one coordinate space and another.