一起学数据结构（2）——线性表及线性表顺序实现
目录
1. 什么是数据结构：
1.1 数据结构的研究内容：
1.2 数据结构的基本概念：
1.2.1 逻辑结构：
1.2.2 存储结构：
2. 线性表：
2.1 线性表的基本定义：
2.2 线性表的运用：
3 .线性表的顺序表示及实现（顺序表）：
3.1 顺序表的概念及结构：
3.2 顺序表的代码实现：
3.2.1 顺序表的创建、初始化及销毁：
3.3 顺序表的四个特殊操作（头插、头删、尾插、尾删）：
3.3.1 尾插：
3.3.2 尾删：
3.3.3 头插：
3.3.4 头删：
3.4 对顺序表的随机位置进行增删操作：
3.4.1 对顺序表的随机位置进行添加数据的操作：
3.4.2 对顺序表的随机位置进行删除数据的操作：
4. 代码总览：
4.1 头文件Seqlist.h:
4.2 函数功能实现文件 Seqlist.c
4.3 测试函数功能文件 test.c:
上一篇文章中，对数据结构中用于评判算法的两个标准，即：时间复杂度、空间复杂度进行简单的介绍及解释。本篇文章，会对：什么是数据结构？数据结构的基本概念进行简单的介绍。着重介绍线性表和线性表的顺序实现。
1. 什么是数据结构：
1.1 数据结构的研究内容：
计算机主要是被用于进行数值计算，这个过程可以分为以下几步：
1.从具体问题中抽象出数学模型。
2.设计相应的算法
3.对程序进行测试，调试等。
对于第一个步骤，也可以分为：分析问题、提取操作对象、找出操作对象之间的关系、用数学语言进行表述这四步。对于提取操作对象和找出操作对象之间的关系这两步，就是数据结构研究的主要内容
1.2 数据结构的基本概念：
首先给出数据结构的定义：
数据结构是相互之间一种或多种特定关系的数据元素的集合。或者说：数据结构是带“结构”的数据元素的集合，"结构“就是指数据元素之间存在的关系。对于数据结构，包含了逻辑结构和存储结构两个层次。
(注：本文只是对数据类型进行简单的介绍，所以，对于下面逻辑结构和存储结构，只给出概念与分类，其中包含的具体内容将会在后续的文章中进行介绍）
1.2.1 逻辑结构：
数据的逻辑结构是指从逻辑关系上描述数据 ，它与数据的存储无关，是独立于计算机的。数据结构的类型如下图所示：
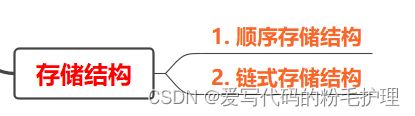
1.2.2 存储结构：
数据对象在计算机中的存储表示称为数据的存储结构，也成为物理结构。数据元素在计算机中有两种基本的存储结构，分别是顺序存储结构和链式存储结构：
2. 线性表：
2.1 线性表的基本定义：
对于线性表，一个很典型的例子就是26英文字母的字母表：
从字母表中可以看出看出线性表的一些性质，例如：虽然线性表中的数据并不相同，但是同一线性表中的元素必定具有相同的特性，即属于同一数据对象。线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。
2.2 线性表的运用：
对于线性表的运用，文章给出两个例子：
例1：一元多项式的运算：
在数学中，一个一元多项通常可以写成下面的形式：
在对一元多项式进行运算之前，首先要知道如何在计算机表示一元多项式。表示一元多项式，便是线性表的一个应用。
通过观察一元多项式可以发现：一元多项式的系数下标，与
的指数相同。因此，可以用线性表来存储一元多项式中各项系数，即：
这时，对于一元多项式中各项中，的指数便隐藏在各项的系数下标中。
此时，假设还有一个一元多项式
，运算与
这两个一元多项式的和，便可以通过上面的思想，用线性表来表示各项系数之和，即：
例子2：稀疏多项式的表示：
给定一个稀疏多项式：
对于稀疏多项式，如果再采用上面存储多项式中各项系数的方法，则需要开辟
个空间，但是上面的多项式，一共只有
个非零元素，所以，采用上面介绍的存储方法，会造成存储空间的极大浪费。
对于稀疏多项式的存储方法，应该存储每一项的系数和指数。如果把稀疏多项式改写成一元多项式的形式，即：
运用线性表对每一项的系数和指数保存，即：
由于本文主要是通过例子来介绍线性表，所以对于稀疏多项式的运算，文章不展开介绍，只给出运算方法及大体的运算规则：
假设由两个稀疏多项式、。对两式进行相加时，需要先创建一个新的数组，假设为C,在运算时，遵从以下规则：
分别从头遍历并且比较两个稀疏多项式，对于
相同的项，则两项系数相加，若系数之和不为
，则在数组C中记录相加项的系数
,对于不同的项，则先将较小的项添加到C中。
3 .线性表的顺序表示及实现（顺序表）：
3.1 顺序表的概念及结构：
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。这种表示也称作线性表的顺序存储结构或顺序映像。特点是：逻辑上相邻的元素，其物理此些许也是相邻的，并且在顺序表中，任一元素都可以随机存取。即：
3.2 顺序表的代码实现：
3.2.1 顺序表的创建、初始化及销毁：
顺序表可以分为两种，分别是：静态顺序表、动态顺序表，对于静态顺序表，其代码表示为：
#define N 100
typedef int SLDataType;
struct Seqlist
{
SLDataType arr[N]; //定长数组
int size; //有效数据个数
}Seqlist; 对于静态顺序表，有一个极大的缺陷，便是内存大小使用不够灵活。比如上面给出的代码，如果需要存储的数据的个数只有几个，则会造成极大的内存空间浪费，如果需要存储的数据的个数大于100，则超出了数组的最大存储范围。所以，为了解决上述问题，在创建顺序表时，一般创建对于内存使用更加灵活的动态顺序表，代码如下：
typedef int SLDataType;
typedef struct Seqlist
{
SLDataType* a; //动态开辟数组的方式，a表示数组首元素地址
size_t size; //数组中有效的数据个数
size_t capacity; //容量大小
}SL;使用动态顺序表后，对于内存空间的使用便灵活很多，例如，编写一个内存空间检查函数，每次向顺序表中添加数据元素时，先通过内存空间检查函数进行检查，当内存空间不够用时，可以通过动态内存管理函数
对已有的内存空间进行增容。
对于顺序表的初始化，将顺序表初始化函数命名为
,函数内容如下：
void SLInit(SL* ps)
{
ps->a = NULL;
ps->size = 0;
ps->capacity = 0;
}上面的代码只是给了初始化函数的大体框架，在实际使用中，并不会把顺序表中的三项内容全都初始化为，而是在初始化时，开辟一定的空间。例如在初始化时，给予
字节大小的空间：
void SLInit(SL* ps)
{
ps->a =(SLDataType*)malloc(sizeof(SLDataType)*4);
if (ps->a == NULL)
{
perror("malloc");
exit (-1);
}
ps->size = 0;
ps->capacity = 4;
}其中的
是动态内存管理函数的一种，对于动态内存管理函数的使用，可以参考下面给出的文章链接中的内容C语言——动态内存管理：_爱写代码的粉毛护理的博客-CSDN博客
语句用于判断是否成功的开辟了空间。
对于动态顺序表的销毁，直接使用
函数对动态开辟的空间进行释放即可。代码如下：
void SLDestroy(SL* ps)
{
free(ps);
ps->a = NULL;
ps->size = ps->capacity = 0;
}3.3 顺序表的四个特殊操作（头插、头删、尾插、尾删）：
3.3.1 尾插：
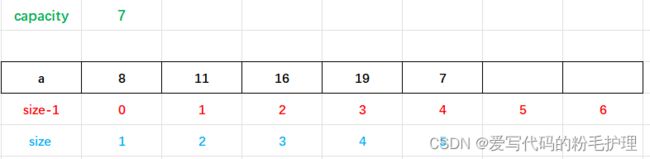
给出一个顺序表，其中的数组中存储的元素如图所示：
由上面对于顺序表的定义可知：
capacity表示顺序表的数组的容量大小
a表示数组，后面的数字表示这个数组中存储的元素
size表示数组中存储元素的个数
size-1用来表示数组下标
对上述数组进行尾插操作，假设第一次插入数字
，则：
进行尾插后，令用来表示数组中存储元素个数的变量
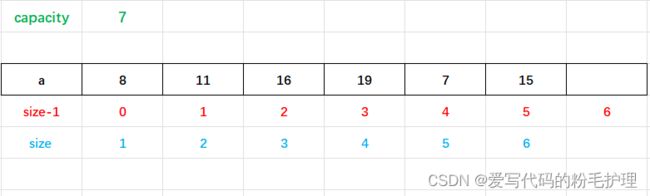
此时，再进行一次尾插，插入数字，则：
进行尾插后，同样令用来表示数组中存储元素格式的变量; 此时，
。表示顺序表中的数组的空间已经被占满，如果还需要进行尾插操作，则需要对数组的空间进行扩容。因为，为了避免上面的情况发生，应该在每次进行尾插操作之前，都对顺序表进行一次检查，如果
,则对数组的空间进行扩容，对于扩容空间的大小，一般扩为原来空间的
倍，代码如下：
void SLPushBack(SL* ps, SLDataType x)
{
if (ps->size == ps->capacity)
{
SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));
if(tmp == NULL)
{
perror("realloc");
}
ps->a = tmp;
ps->capacity = ps->capacity * 2;
}
ps->a[ps->size] = x;
ps->size++;
}对于上面给出的尾插代码，最核心的部分就是对内存空间进行扩容，即：
SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));对于理解用于扩容的代码，需要将内存空间和
的概念分清，只是代表了已经开辟的内存空间的个数，不会反应内存空间的大小，因此，在上面用于扩容的代码中，
只是表示将内存空间的数量扩大到倍，想到达到对内存空间的大小扩容到倍，需要再乘上存储的数据的类型，即
（注：对于用于扩容的函数，也可以在下面给出的文章中进行了解C语言——动态内存管理：_爱写代码的粉毛护理的博客-CSDN博客）
如果已经掌握了对动态内存管理函数的初步使用，会发现，尾插的代码中，再对内存空间进行扩容后，并没有用函数去释放内存空间。这是因为函数的返回值的特殊性质。这个性质同样也可以在上面给出的文章链接中进行了解，在本文中会进行简要的解释：
上面提到的函数的返回值的特殊性质，即：原地扩容、异地扩容。
对于原地扩容，如果对内存进行扩容时，后面有足够多的内存空间可以达到对已有内存空间进行扩容的目的，则函数返回值返回已有空间的首地址。
对于异地扩容，如果对内存进行扩容时，后面没有足够多的内存空间可以达到对已有内存空间进行扩容的目的，则函数会寻找一个新的空间，这个空间的地址是随机的，并且返回值返回这个新空间的首地址。这两个性质，可以由下面的代码进行演示：
int main()
{
int* p1 = (int*)malloc(12);
int* p2 = (int*)realloc(p1, 2);
printf("%p %p\n",p1, p2);
int* p3 = (int*)malloc(10);
int* p4 = (int*)realloc(p3, 200);
printf("%p %p",p3, p4);
return 0;
}结果如下：
可以验证，
的地址表示，此时是原地扩。
此时，
地址不同，是异地扩。
所以，函数对于扩容时不同情况的处理很灵活，不需要在扩容后用函数释放内存空间。为了测试尾插的功能是否正常，封装一个函数，插入
这几个数字：
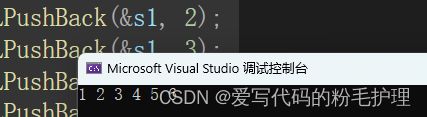
void test1()
{
SL s1;
SLInit(&s1);
SLPushBack(&s1, 1);
SLPushBack(&s1, 2);
SLPushBack(&s1, 3);
SLPushBack(&s1, 4);
SLPushBack(&s1, 5);
SLPushBack(&s1, 6);
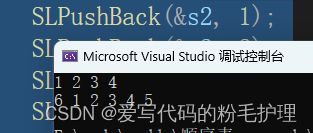
SLPrint(&s1);
}结果如下：
3.3.2 尾删：
尾删就是从末尾向前删除元素，原理比较简单，只需要让
即可
//尾删：
void SLPopBack(SL* ps)
{
ps->size--;
}利用下面的代码测试尾删的功能：
void test1()
{
SL s1;
SLInit(&s1);
SLPushBack(&s1, 1);
SLPushBack(&s1, 2);
SLPushBack(&s1, 3);
SLPushBack(&s1, 4);
SLPushBack(&s1, 5);
SLPushBack(&s1, 6);
SLPopBack(&s1);
SLPopBack(&s1);
SLPrint(&s1);
}结果如下：
3.3.3 头插：
在执行尾插操作时说到，每次插入前，需要检查以下数组的内存空间是否足够。在头插中，同样需要对内存空间进行检查，所以，为了方便操作，不如将尾插中用于检查数组内存空间的代码封装成一个函数。
void SLCheckCapacity(SL* ps)
{
if (ps->size == ps->capacity)
{
SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));
if (tmp == NULL)
{
perror("realloc");
}
ps->a = tmp;
ps->capacity = ps->capacity * 2;
}
}对于头插，只需要将已有的元素全部向后移动一位，再把想要插入的元素插入到数组的首个位置。此时，因为插入了一个元素，所以，顺序表中的
+1例如，头插一个数字
，可以用图表示为：
原数组：
全部元素向后挪动一位：
头插数字 ：
将上述过程用代码表示：
void SLPushFront(SL* ps, SLDataType x)
{
SLCheckCapacity(ps);
int end = ps->size - 1;
while (end >= 0)
{
ps->a[end+1] = ps->a[end];
end--;
}
ps->a[0] = x;
ps->size++;
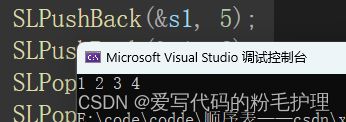
}用下列函数对头插功能进行设置：
void test2()
{
SL s2;
SLInit(&s2);
SLPushBack(&s2, 1);
SLPushBack(&s2, 2);
SLPushBack(&s2, 3);
SLPushBack(&s2, 4);
SLPushBack(&s2, 5);
SLPushFront(&s2, 6);
SLPrint(&s2);
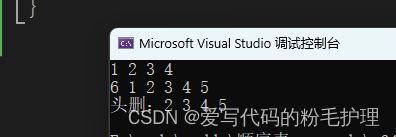
}结果如下：
（注：第一行的
是测试尾插的结果，头插的结果是第一行）
3.3.4 头删：
头删的过程与头插相反，进行头插的操作时，需要把元素整体向后移动，且移动的顺序是从后向前，对于头删，则是需要从前向后一次覆盖前面的数据。
void SLPopFront(SL* ps)
{
if (ps->size == 0)
{
return;
}
int start = 0;
int end = ps->size - 1;
while (start <= end)
{
ps->a[start] = ps->a[start+1];
start++;
}
ps->size--;
}用下面的函数测试头删的功能：
void test3()
{
SL s3;
SLInit(&s3);
SLPushBack(&s3, 1);
SLPushBack(&s3, 2);
SLPushBack(&s3, 3);
SLPushBack(&s3, 4);
SLPushBack(&s3, 5);
SLPopFront(&s3);
printf("头删：");
SLPrint(&s3);
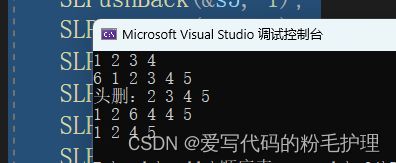
}结果如下：
3.4 对顺序表的随机位置
进行增删操作：
3.4.1 对顺序表的随机位置进行添加数据的操作：
对随机位置添加数据的操作，与头插的操作流程相似。基本可以分为以下几步：
1.判断这个位置对于数组下标而言是否合法，即
2.将位置以及后面的元素整体后移动一位。
3.将新的元素插入到数组中下标为
的位置
4.将
用图来表示上述过程，及：
将位置以及后续元素向后移动一位：
最后，向位置为的地方插入元素即可。因为多插入了一个元素，最后需要
代码如下：
void SLInsert(SL* ps, size_t i, SLDataType x)
{
if (i < 0 || i >(ps->size - 1))
{
printf("坐标非法");
exit(-1);
}
size_t end = ps->size - 1;
for (size_t end = ps->size - 1; end > i-1; end--)
{
ps->a[end + 1] = ps->a[end];
}
ps->a[i - 1] = x;
ps->size++;
}用下面的代码验证随机位置插入功能是否正常：
void test4()
{
SL s4;
SLInit(&s4);
SLPushBack(&s4, 1);
SLPushBack(&s4, 2);
SLPushBack(&s4, 3);
SLPushBack(&s4, 4);
SLPushBack(&s4, 5);
SLInsert(&s4, 3, 6);
SLPrint(&s4);
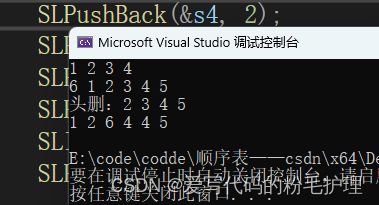
}结果如下：
（注：结果是最后一行数字所展示的效果）
3.4.2 对顺序表的随机位置进行删除数据的操作：
对于在顺序表的随机位置删除数据的操作可以分为以下几步：
1.检查位置对于数组下标是否合理，即
2.将位置后面的元素整体向前移动一位。
3. 因为删除了一个元素，所以
将上述过程用图进行表示：
将位置后面的元素整体向前移动一位：
最后
将上述过程用代码表示：
void SLErase(SL* ps, size_t i)
{
if (i <= 0 || (i > ps->size - 1))
{
printf("坐标非法");
}
size_t start = i-1;
while (start <= ps->size - 1)
{
ps->a[start] = ps->a[start + 1];
start++;
}
ps->size--;
}用下面的函数测试功能：
void test5()
{
SL s5;
SLInit(&s5);
SLPushBack(&s5, 1);
SLPushBack(&s5, 2);
SLPushBack(&s5, 3);
SLPushBack(&s5, 4);
SLPushBack(&s5, 5);
SLErase(&s5, 3);
SLPrint(&s5);
}结果如下：
（注：最后一行的数字对应着测试的功能的结果）
4. 代码总览：
4.1 头文件Seqlist.h:
#include
#include
#include
//#define N 100
//typedef int SLDataType;
//struct Seqlist
//{
// SLDataType arr[N];
// int size;
//}Seqlist;
typedef int SLDataType;
typedef struct Seqlist
{
SLDataType* a;
size_t size;
size_t capacity;
}SL;
//用于打印测试：
void SLPrint(SL* ps);
//用于初始化顺序表
void SLInit(SL* ps);
//用于销毁顺序表：
void SLDestroy(SL* ps);
//尾插：
void SLPushBack(SL* ps, SLDataType x);
//尾删
void SLPopBack(SL* ps);
//检测内存空间
void SLCheckCapacity(SL* ps);
//头插
void SLPushFront(SL* ps, SLDataType x);
//头删
void SLPopFront(SL* ps);
//随机位置插入
void SLInsert(SL* ps,size_t i ,SLDataType x);
//随机位置删除
void SLErase(SL* ps, size_t i);
4.2 函数功能实现文件 Seqlist.c
#include"Seqlist.h"
//初始化顺序表
void SLInit(SL* ps)
{
ps->a =(SLDataType*)malloc(sizeof(SLDataType)*4);
if (ps->a == NULL)
{
perror("malloc");
exit (-1);
}
ps->size = 0;
ps->capacity = 4;
}
//销毁顺序表
void SLDestroy(SL* ps)
{
free(ps->a);
ps->a = NULL;
ps->size = ps->capacity = 0;
}
//尾插：
void SLPushBack(SL* ps, SLDataType x)
{
SLCheckCapacity(ps);
ps->a[ps->size] = x;
ps->size++;
}
//用于打印数据
void SLPrint(SL* ps)
{
int i = 0;
for (i = 0; i < ps->size; i++)
{
printf("%d ", ps->a[i]);
}
printf("\n");
}
//尾删：
void SLPopBack(SL* ps)
{
ps->size--;
}
//检查内存空间：
void SLCheckCapacity(SL* ps)
{
if (ps->size == ps->capacity)
{
SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));
if (tmp == NULL)
{
perror("realloc");
}
ps->a = tmp;
ps->capacity = ps->capacity * 2;
}
}
//头插
void SLPushFront(SL* ps, SLDataType x)
{
SLCheckCapacity(ps);
int end = ps->size - 1;
while (end >= 0)
{
ps->a[end+1] = ps->a[end];
end--;
}
ps->a[0] = x;
ps->size++;
}
//头删：
void SLPopFront(SL* ps)
{
if (ps->size == 0)
{
return;
}
int start = 0;
int end = ps->size - 1;
while (start <= end)
{
ps->a[start] = ps->a[start+1];
start++;
}
ps->size--;
}
//随机位置插入：
void SLInsert(SL* ps, size_t i, SLDataType x)
{
if (i < 0 || i >(ps->size - 1))
{
printf("坐标非法");
exit(-1);
}
size_t end = ps->size - 1;
for (size_t end = ps->size - 1; end > i-1; end--)
{
ps->a[end + 1] = ps->a[end];
}
ps->a[i - 1] = x;
ps->size++;
}
//随机位置删除：
void SLErase(SL* ps, size_t i)
{
if (i <= 0 || (i > ps->size - 1))
{
printf("坐标非法");
}
size_t start = i-1;
while (start <= ps->size - 1)
{
ps->a[start] = ps->a[start + 1];
start++;
}
ps->size--;
}4.3 测试函数功能文件 test.c:
#include"Seqlist.h"
void test1()
{
SL s1;
SLInit(&s1);
SLPushBack(&s1, 1);
SLPushBack(&s1, 2);
SLPushBack(&s1, 3);
SLPushBack(&s1, 4);
SLPushBack(&s1, 5);
SLPushBack(&s1, 6);
SLPopBack(&s1);
SLPopBack(&s1);
SLPrint(&s1);
}
void test2()
{
SL s2;
SLInit(&s2);
SLPushBack(&s2, 1);
SLPushBack(&s2, 2);
SLPushBack(&s2, 3);
SLPushBack(&s2, 4);
SLPushBack(&s2, 5);
SLPushFront(&s2, 6);
SLPrint(&s2);
}
void test3()
{
SL s3;
SLInit(&s3);
SLPushBack(&s3, 1);
SLPushBack(&s3, 2);
SLPushBack(&s3, 3);
SLPushBack(&s3, 4);
SLPushBack(&s3, 5);
SLPopFront(&s3);
printf("头删：");
SLPrint(&s3);
}
void test4()
{
SL s4;
SLInit(&s4);
SLPushBack(&s4, 1);
SLPushBack(&s4, 2);
SLPushBack(&s4, 3);
SLPushBack(&s4, 4);
SLPushBack(&s4, 5);
SLInsert(&s4, 3, 6);
SLPrint(&s4);
}
void test5()
{
SL s5;
SLInit(&s5);
SLPushBack(&s5, 1);
SLPushBack(&s5, 2);
SLPushBack(&s5, 3);
SLPushBack(&s5, 4);
SLPushBack(&s5, 5);
SLErase(&s5, 3);
SLPrint(&s5);
}
int main()
{
test1();
test2();
test3();
test4();
test5();
return 0;
}