概率论与数理统计——多方法解决-双样本方差的F检验-Excel/SPSS
本篇将结合一个例题,借助Excel工具和SPSS,分别从不同的拒绝域位置和利用不同的函数,多方法地总结双样本的F检验的思路和方法。
参数假设检验的内容请参考《概率论与数理统计——参数假设检验》
多方法解决-双样本方差的F检验
- 解法一:双尾检验+比较统计量
-
- 第一步
- 第二步
- 第三步
- 第四步
- 解法二:双尾检验+比较统计量的概率
-
- 第四步
- 解法三:左右单尾检验结合+比较统计量
-
- 第一次检验:右单尾检验
- 第一步
- 第二步
- 第三步
- 第四步
- 第二次检验:左单尾检验
- 第一步
- 解法四:左右单尾检验结合+比较统计量的概率
- 解法五:利用Excel的数据分析工具
- 解法六:利用SPSS进行F检验
- 总结
【例题】
有A、B两个语料库,从中各抽取5篇,分别统计出每篇的句数,假设两个语料库的语篇句数是正态分布,以0.05的显著水平来检验两个语料库的语篇句数的变异程度是否一致。
| A | 20 | 18 | 12 | 24 | 26 |
|---|---|---|---|---|---|
| B | 24 | 22 | 18 | 22 | 14 |
要想检验两个样本的变异程度是否一致,就要看二者的方差是否一致,显然采用F检验。
解法一:双尾检验+比较统计量
第一步
根据问题的要求提出:
原 假 设 H 0 : σ 1 σ 2 = 1 备 择 假 设 H 1 : σ 1 σ 2 ≠ 1 原假设H_0:\frac{\sigma_1}{\sigma_2}=1\ \ \ \ \ \ 备择假设H_1:\frac{\sigma_1}{\sigma_2} \neq 1 原假设H0:σ2σ1=1 备择假设H1:σ2σ1=1
第二步
构造统计量:
F = S 1 2 / S 2 2 σ 1 2 / σ 2 2 F=\frac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2} F=σ12/σ22S12/S22
代入数据:
F = 4 2 / 3.5 8 2 1 = 1.25 F=\frac{4^2/3.58^2}{1}=1.25 F=142/3.582=1.25
第三步
设定显著水平:
α = 0.05 \alpha=0.05 α=0.05
第四步
该检验是双尾检验,利用Excel的FINV()函数,求得两个临界点为:
F α 2 = 9.065 F 1 − α 2 = 0.104 F_\frac{\alpha}{2}=9.065 \\ F_{1-\frac{\alpha}{2}}=0.104 F2α=9.065F1−2α=0.104
比较可得:
0.104 < 1.25 < 9.065 0.104<1.25<9.065 0.104<1.25<9.065
即:
F 1 − α 2 < F < F α 2 F_{1-\frac{\alpha}{2}}
故,统计量位于接受域。因此,拒绝 H 1 H_1 H1,接受 H 0 H_0 H0。
结论为:95%的把握肯定, A、B语料库的语篇句数的变异程度一致。
解法二:双尾检验+比较统计量的概率
前三步参考解法一
第四步
该检验是双尾检验,利用Excel的FTEST()函数,求得双尾概率为:
P ( F ) = 0.83 P(F)=0.83 P(F)=0.83
FTEST(array1,array2)函数返回的是F检验array1 和 array2 中的方差没有显著差异的双尾概率。
本方法的使用语句为:=FTEST({20,18,12,24,16},{24,22,18,22,14})。当然,在实际的操作中,可以将两个数组替换为对应的表格区域。
比较可得:
0.025 < 0.83 < 0.975 0.025<0.83<0.975 0.025<0.83<0.975
即:
P ( F 1 − α 2 ) < P ( F ) < P ( F α 2 ) P(F_{1-\frac{\alpha}{2}})
故,统计量位于接受域。因此,拒绝 H 1 H_1 H1,接受 H 0 H_0 H0。
结论为:95%的把握肯定, A、B语料库的语篇句数的变异程度一致。
解法三:左右单尾检验结合+比较统计量
这个方法的思路是,进行两次单尾检验,从而检验出 σ 1 σ 2 ≤ 1 \frac{\sigma_1}{\sigma_2}\le 1 σ2σ1≤1和 σ 1 σ 2 ≥ 1 \frac{\sigma_1}{\sigma_2}\ge 1 σ2σ1≥1同时显著成立,进而推导出 σ 1 σ 2 = 1 \frac{\sigma_1}{\sigma_2}=1 σ2σ1=1显著成立。
第一次检验:右单尾检验
第一步
根据问题的要求提出:
原 假 设 H 0 : σ 1 σ 2 ≤ 1 备 择 假 设 H 1 : σ 1 σ 2 > 1 原假设H_0:\frac{\sigma_1}{\sigma_2}\le 1\ \ \ \ \ \ 备择假设H_1:\frac{\sigma_1}{\sigma_2} > 1 原假设H0:σ2σ1≤1 备择假设H1:σ2σ1>1
第二步
构造统计量:
F = S 1 2 / S 2 2 σ 1 2 / σ 2 2 F=\frac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2} F=σ12/σ22S12/S22
代入数据:
F = 4 2 / 3.5 8 2 1 = 1.25 F=\frac{4^2/3.58^2}{1}=1.25 F=142/3.582=1.25
第三步
设定显著水平:
α = 0.05 \alpha=0.05 α=0.05
第四步
该检验是右尾检验,利用Excel的FINV()函数,求得临界点为:
F α = 6.388 F_\alpha=6.388 Fα=6.388
比较可得:
1.25 < 6.388 1.25<6.388 1.25<6.388
即:
F < F α F
故,统计量位于接受域。因此,拒绝 H 1 H_1 H1,接受 H 0 H_0 H0。
结论为:95%的把握肯定, σ 1 σ 2 ≤ 1 \frac{\sigma_1}{\sigma_2}\le 1 σ2σ1≤1。
第二次检验:左单尾检验
第一步
根据问题的要求提出:
原 假 设 H 0 : σ 1 σ 2 ≥ 1 备 择 假 设 H 1 : σ 1 σ 2 < 1 原假设H_0:\frac{\sigma_1}{\sigma_2}\ge 1\ \ \ \ \ \ 备择假设H_1:\frac{\sigma_1}{\sigma_2} < 1 原假设H0:σ2σ1≥1 备择假设H1:σ2σ1<1
第二步至第四步类比参考第一次检验
最后可以得到结论为:95%的把握肯定, σ 1 σ 2 ≥ 1 \frac{\sigma_1}{\sigma_2}\ge 1 σ2σ1≥1。
综合两次的检验结果可得:95%的把握肯定, σ 1 σ 2 = 1 \frac{\sigma_1}{\sigma_2}= 1 σ2σ1=1,即 A、B语料库的语篇句数的变异程度一致。
解法四:左右单尾检验结合+比较统计量的概率
该解法的思路和解法三基本相同,只是在检验时,比较的是统计量的概率。
统计量的概率可以通过FDIST()函数来实现。
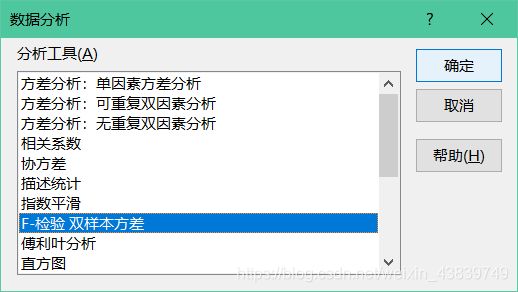
解法五:利用Excel的数据分析工具
该解法的思路是利用Excel的数据分析工具,得到双尾概率的单侧概率,进而将单侧概率与 α 2 \frac{\alpha}{2} 2α比较,进而得出结论。
然后在弹出的对话框里输入所要分析的两组数据的区域,并填写好参数 α \alpha α,选择好输出的位置,点击确定。
注意,此时我们需要的是双尾的单侧概率,此时的参数 α \alpha α应当是实际的 α 2 = 0.025 \frac{\alpha}{2}=0.025 2α=0.025。
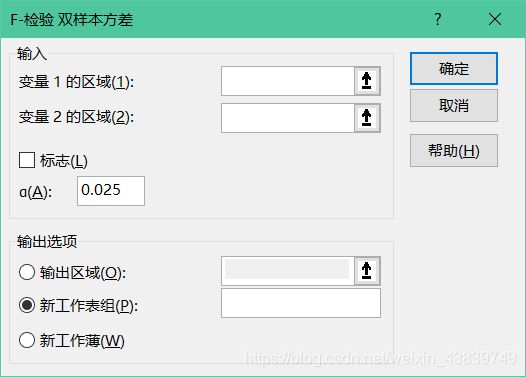
然后会产生下面的表格:
F-检验 双样本方差分析
| - | 变量1 | 变量2 |
|---|---|---|
| 平均 | 18 | 20 |
| 方差 | 20 | 16 |
| 观测值 | 5 | 5 |
| d f df df | 4 | 4 |
| F F F | 1.25 | |
| P ( F ≤ f ) P(F\le f) P(F≤f) | 0.41701 | |
| F F F单尾临界 | 9.60453 |
小数点的位数会根据单元格的数值格式的设定变化,并非产生的一定就是表中小数体现的位数。
先解释一下表里面的数据的含义,均值和方差不必多数;这里的观测值是样本的个数; d f df df是自由度,为样本的个数减一; F F F即根据公式构造的统计量的值; P ( F ≤ f ) P(F\le f) P(F≤f)即 F F F的单侧概率,相当于FTEST({20,18,12,24,16},{24,22,18,22,14})/2的结果; F F F单尾临界是指双尾检验的一尾的临界点。
所以,比较可得:
0.41701 > 0.025 0.41701>0.025 0.41701>0.025
故,拒绝 H 1 H_1 H1,接受 H 0 H_0 H0,即 σ 1 σ 2 = 1 \frac{\sigma_1}{\sigma_2}= 1 σ2σ1=1。
因此,有95%的把握肯定AB两个语料库的变异程度显著一致。
解法六:利用SPSS进行F检验
既然进行统计检验,当然少不了专业的SPSS。
用SPSS检验的结果如下:

其中 S i g > 0.05 Sig>0.05 Sig>0.05显然成立,因此可以判定两组数据的方差显著一致。
在SPSS中检验出的结果是1,也就是表明两组数据方差非常一致,几乎没有差别。例题的数据只是一个示例,并不符合实际的数据情况。
总结
这六种方法主要是从不同的软件出发,分别利用双尾检验或左右单尾检验的方式完成F检验,其中涉及到使用不同的Excel函数和Excel工具,这些函数和工具各有千秋,可以根据实际需求选择合适的方案。