数据结构与算法分析-C++描述 第4章 二叉树ADT（二叉查找树）

       二叉树（binary tree）是一棵每个节点都不能多于两个子节点的树。其递归结构如图所示：

       二叉树的一个性质是平均二叉树的深度要比节点个数N小得多，分析表明，这个深度是,对于特殊类型的二叉树，即二叉查找树（binary search tree），其深度的平均值为 。

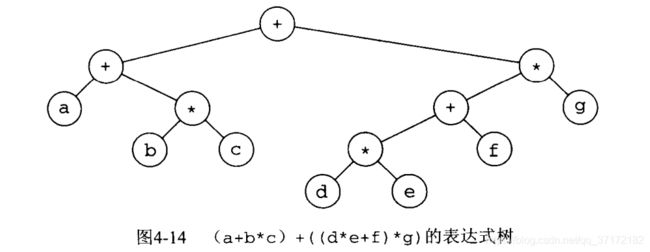
       二叉树有许多与搜索无关的重要应用，主要应用之一是在编译器的设计领域，一个例子--表达树（如图4-14）

可以通过中序遍历实现中缀表达式，可以通过后序遍历实现后缀表达式 。

       二叉查找树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。

        二叉查找树的性质：1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
                                         2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
                                         3）任意节点的左、右子树也分别为二叉查找树；
                                         4）没有键值相等的节点；

     实例：二叉查找树的常用遍历：前序遍历、中序遍历、后序遍历；增加、删除、打印、清空方法；最大值、最小值、前驱节点、后驱节点等。

1、tree.h

//tree.h
#ifndef TREE_H_
#define TREE_H_

#include 
#include

using namespace std;

template
struct Node{
	dataType data;
	Node *left;
	Node *right;
	Node *parent;
	Node(dataType &d, Node *l, Node *r, Node *p):data(d), left(l), right(r), parent(p){};
};

template
class Tree{
private:
	Node *root;
public:
	Tree():root(NULL){};
	~Tree()
	{
		destroy();
	};
	void preOrder()
	{	
		preOrder(root);
	};
	void inOrder()
	{
		inOrder(root);
	};
	void postOrder()
	{
		postOrder(root);
	};
	Node* search(dataType d)
	{
		search(root, d);
	};
	Node* iterativeSearch(dataType d)
	{
		iterativeSearch(root, d);
	}
	dataType min()
	{
		Node *node = min(root);
		if(node != NULL)
		{
			return node -> data;
		}
		return (dataType)NULL;
	};
	
	dataType max()
	{
		Node *node = max(root);
		if(node != NULL)
		{
			return node -> data;
		}
		return (dataType)NULL;
	};
	
	//successor : min node bigger than the given node
	Node* successor(Node *node)
	{
		//if node has right child, successor is the min node bigger than given node itself
		if(node -> right != NULL)
		{
			return min(node -> right);
		}
		//if not, case 1 node is left child, successor is the parent node
		Node *temp = node -> parent;
		//case 2 : node is right child, successor is the lowest parent node
		while(temp != NULL && node == temp -> right)
		{
			node = temp;
			temp = temp -> parent;
		}
		return temp;
	};
	
	//presuccessor : max node less than the given node
	Node* presuccessor(Node *node)
	{
		//if node has left child, presuccessor is the max node in given node
		if(node -> left != NULL)
		{
			return max(node -> left);
		}
		//if not, #1 node is right child, presuccessor is the parent node, #2 presuccessor the lowest parent node
		Node *temp = node -> parent;
		while(temp != NULL && node == temp -> left)
		{
			node = temp;
			temp = temp -> parent;
		} 
		return temp;
	};
	
	void insert(dataType d)
	{
		Node *temp = NULL;
		if((temp = new Node(d, NULL, NULL, NULL)) == NULL)
		{
			return;
		}
		insert(root, temp);
	};
	void remove(dataType d)
	{
		Node *temp, *node;
		//judge whether d is in the Tree
		if(((temp = search(root, d))) != NULL)
		{
			if((node = remove(root, temp)) != NULL)
			{
				delete node;
			}
		}
		
	};
	void destroy()
	{
		destroy(root);
	};
	void print()
	{
		if(root != NULL)
		{
			print(root, root -> data, 0);
		}
	};
private:
	void preOrder(Node *node) const;
	void inOrder(Node *node) const;
	void postOrder(Node *node) const;
	Node* search(Node *node, dataType d) const;
	Node* iterativeSearch(Node *node, dataType d) const;
	Node* min(Node *node);
	Node* max(Node *node);
	void insert(Node* &node, Node *d);
	Node* remove(Node* &node, Node *d);
	void destroy(Node* &node);
	void print(Node *node, dataType d, int direction);
};

//preOrder : root -> left -> right
template
void Tree::preOrder(Node *node) const
{
	if(node != NULL)
	{
		cout << node -> data << " ";
		preOrder(node -> left);
		preOrder(node -> right);
	}
}

//inOrder : left -> root -> right
template
void Tree::inOrder(Node *node) const
{
	if(node != NULL)
	{
		inOrder(node -> left);
		cout << node -> data << " ";
		inOrder(node -> right);
	}
}

//postOrder : left -> right -> root
template
void Tree::postOrder(Node *node) const
{
	if(node != NULL)
	{
		postOrder(node -> left);
		postOrder(node -> right);
		cout << node -> data << " ";
	}
}

//binary search without iteration
template
Node* Tree::search(Node *node, dataType d) const
{
	if(node == NULL || node -> data == d)
	{
		return node;
	}
	if(d < node -> data)
	{
		search(node -> left, d);
	}
	else
	{
		search(node -> right, d);
	}
}


//binary search with iteration
template
Node* Tree::iterativeSearch(Node *node, dataType d) const
{
	while((node != NULL) && (node -> data != d))
	{
		if(d < node -> data)
		{
			iterativeSearch(node -> left, d);
		}
		else
		{
			iterativeSearch(node -> right, d);
		}
	}
	return node;
}

//find the minimum node in Tree (left -> .. -> left)
template
Node* Tree::min(Node *node)
{
	if(node == NULL)
	{
		return node;
	}
	while(node -> left != NULL)
	{
		node = node -> left;
	}
	return node;
}

//find the maxmium node in Tree (right -> ... -> right)
template
Node* Tree::max(Node *node)
{
	if(node == NULL)
	{
		return node;
	}
	while(node -> right != NULL)
	{
		node = node -> right;
	}
	return node;
}

//insert data into Tree
template
void Tree::insert(Node* &node, Node *d)
{
	Node *temp = NULL;
	Node *n = node;
	//judge the position of d
	while(n != NULL)
	{
		temp = n;
		//update left part if d < temp
		if(d -> data < temp -> data)
		{
			n = n -> left;
		}
		//update right part if d > temp
		else
		{
			n = n -> right;
		}
	}
	//insert node		
	d -> parent = temp;
	if(temp == NULL)
	{
		node = d;
	}
	else if(d -> data < temp -> data)
	{
		temp -> left = d;
	}
	else
	{
		temp -> right = d;
	}
}

//remove node d from node
template
Node* Tree::remove(Node* &node, Node *d)
{
	Node *temp1 = NULL;
	Node *temp2 = NULL;
	if((d -> left == NULL) || (d -> right == NULL))
	{
		temp2 = d;
	}
	else
	{
		temp2 = successor(d);
	}
	if(temp2 -> left != NULL)
	{
		temp1 = temp2 -> left;
	}
	else
	{
		temp1 = temp2 -> right;
	}
	if(temp1 != NULL)
	{
		temp1 -> parent = temp2 -> parent;
	}
	if(temp2 -> parent == NULL)
	{
		node = temp1;
	}
	else if(temp2 == temp2 -> parent -> left)
	{
		temp2 -> parent -> left = temp1;
	}
	else
	{
		temp2 -> parent -> right = temp1;
	}
	if(temp2 != d)
	{
		d -> data = temp2 -> data;
	}
	return temp2;
}

//destroy the Tree
template
void Tree::destroy(Node* &node)
{
	if(node == NULL)
	{
		return;
	}
	if(node -> left != NULL)
	{
		destroy(node -> left);
	}
	if(node -> right != NULL)
	{
		destroy(node -> right);
	}
	delete node;
	node = NULL;
}

//print the Tree structure
template
void Tree::print(Node *node, dataType d, int direction)
{
	if(node != NULL)
	{
		//root : direction = 0
		if(direction == 0)
		{
			cout << setw(2) << node -> data << " is root " << endl;	
		}
		else
		{
			cout << setw(2) << node -> data << " is " << d << " 's " << setw(12) << (direction == 1 ? " right child " : " left child ") << endl;
		}
		// left : direction = -1
		print(node -> left, node -> data, -1);
		//right : direction = 1
		print(node -> right, node -> data, 1);
	}
}

#endif

2、main.cpp

//main.cpp
#include
#include"tree.h"

using namespace std;

int main()
{
	int arr[8] = {5, 3, 2, 7, 4, 8, 1, 6};
	Tree *tree = new Tree();
	cout << "******* insert *******" << endl;
	for(int i = 0; i < 8; i++)
	{
		tree -> insert(arr[i]);
	}
	cout << "******* print *******" << endl;
	tree -> print();
	
	cout << "******* preOrder *******" << endl;
	tree -> preOrder();
	cout << endl;
	
	cout << "******* inOrder *******" << endl;
	tree -> inOrder();
	cout << endl;
	
	cout << "******* postOrder *******" << endl;
	tree -> postOrder();
	cout << endl;
	
	cout << "******* min *******" << endl;
	cout << "the min data in Tree is " << tree -> min() << endl;
	
	cout << "******* max *******" << endl;
	cout << "the max data in Tree is " << tree -> max() << endl;
	
	cout << "******* remove *******" << endl;
	tree -> remove(4);
	
	cout << "******* inOrder *******" << endl;
	tree -> inOrder();
	cout << endl;
	
	cout << "******* destroy *******" << endl;
	tree -> destroy();
	
	cout << "done " << endl;
	return 0;
}

practice makes perfect!

参考博客：二叉查找树(二)之 C++的实现