Java版二叉树的前序遍历查找、中序遍历查找和后序遍历查找
文章收藏的好句子:任何挫折,如果无法彻底击败你,那一定会使你更强。
目录
1、二叉树的节点查找
1、1 前序遍历查找
1、2 中序遍历查找
1、3 后序遍历查找
1、二叉树的节点查找
1、1 前序遍历查找
在Java版的数据结构和算法(四)这篇文章中,我们学了二叉树的前序遍历、中序遍历和后序遍历,有了前面的基础,本篇文章我们就来说说二叉树的前序遍历查找、中序遍历查找和后序遍历查找,那么看起这篇文章来就会相对好理解很多。
这里我们先说说前序遍历的查找思路:
(1)先判断当前结点的数值是否等于要查找节点的数值,如果相等,则返回当前结点;如果不相等,则判断当前结点的左子节点是否为空。
(2)如果当前节点的左子节点不为空,则向左子节点递归前序查找。
(3)如果左子节点递归前序查找能找到该结点,则返回;否继续判断,当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找;如果查找完一整棵树还是没有找到,则返回 null。
看到这里,有的读者可能会说,我还是很懵啊,没关系,我们这里举个例子,上面的前序遍历的查找思路就更清晰了;我们先画出一颗二叉树,如图1所示:
首先我们画的图1这棵二叉树是有规则的,你们看父节点的序号都比子节点的序号小,同一父节点的左子节点比右子节点小;好,假设我们这里要找序号为5的人物,我们来列举一下查找步骤:
(1)一开始将要查找的节点的序号对比根节点的序号,发现1不等于5,于是往根节点的左子节点进行递归前序查找。
(2)将根节点的左子节点的序号(序号为2)和要查找的节点的序号进行对比,发现2不等于5,于是将序号为2的节点的左子节点(序号为4)进行递归前序查找。
(3)将该节点(序号为4)的序号与要查找的节点的序号进行对比,发现4不等于5,又发现序号为4的节点是叶子节点,于是结束序号为4的节点的递归前序遍历。
(4)到了这里,序号为2的节点的左子节点的递归前序查找已经结束了,于是进行序号为2的节点的右子节点(序号为5)的递归前序查找,发现序号为2的节点的右子节点的序号于要查找的节点的序号相等,最终将序号为2的节点的右子节点返回,结束查找。
假设我们要前序查找去找一个不存在的人物呢?比如说序号为8的人物,它的查找思路跟查找序号为5的节点的思路是一样的,只是查找序号为5的节点不用遍历图1中的整棵树进行查找,而查找序号为8的节点则需要遍历图1中的整棵树进行查找,这里我不再列举查找序号为8的人物的前序遍历查找思路。
好了,我们这里用代码实现一把,分别用前序遍历查找去找序号为5和序号为8的人物;
(1)写一个节点类 FigureNode :
public class FigureNode {
private int no;
private String name;
private FigureNode left;
private FigureNode right;
public FigureNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
public String getName() {
return name;
}
public int getNo() {
return no;
}
public FigureNode getLeft() {
return left;
}
public void setLeft(FigureNode left) {
this.left = left;
}
public FigureNode getRight() {
return right;
}
public void setRight(FigureNode right) {
this.right = right;
}
}(2)写一个测试类 Test :
public class Test {
private FigureNode root;
public static void main(String[] args) {
Test test = new Test();
test.createBinaryTree();
test.preOrderSeach(5);
System.out.println("*****************");
test.preOrderSeach(8);
}
// 创建一棵二叉树
private void createBinaryTree() {
FigureNode figureNode = new FigureNode(1,"如来佛祖");
FigureNode figureNode2 = new FigureNode(2,"观音菩萨");
FigureNode figureNode3 = new FigureNode(3,"牛魔王");
FigureNode figureNode4 = new FigureNode(4,"孙悟空");
FigureNode figureNode5 = new FigureNode(5,"猪八戒");
FigureNode figureNode6 = new FigureNode(6,"红孩儿");
FigureNode figureNode7 = new FigureNode(7,"铁扇公主");
root = figureNode;//根节点的人物是如来佛祖
root.setLeft(figureNode2);//根节点的左子节点是序号为2的节点
root.setRight(figureNode3);//根节点的右子节点是序号为3的节点
figureNode2.setLeft(figureNode4);//序号为2的左子节点是序号为4的节点
figureNode2.setRight(figureNode5);//序号为2的右子节点是序号为5的节点
figureNode3.setLeft(figureNode6);//序号为3的左子节点是序号为6的节点
figureNode3.setRight(figureNode7);//序号为3的右子节点是序号为7的节点
}
// 前序遍历查找,以根节点为当前节点进行查找
private void preOrderSeach(int no) {
if (root != null) {
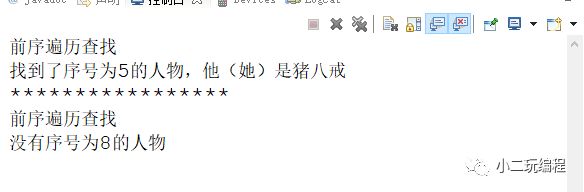
System.out.println("前序遍历查找");
FigureNode result = preOrderSeach(root, no);
if (result == null) {
System.out.println("没有序号为" + no + "的人物");
} else {
System.out.println("找到了序号为" + no + "的人物,他(她)是"
+ result.getName());
}
} else {
System.out.println("这是一棵空的二叉树");
}
}
// 前序遍历查找
private FigureNode preOrderSeach(FigureNode node, int no) {
if (node.getNo() == no) {// 比较当前节点
return node;
}
FigureNode res = null;
// 判断当前节点的左子节点是否为空
if (node.getLeft() != null) {
// 左递归前序查找 找到节点 则返回
res = preOrderSeach(node.getLeft(), no);// 递归前序查找
}
// 如果不为空说明进行 “左递归前序查找” 时查找到了该节点
if (res != null) {
return res;
}
// 当前的结点的右子节点是否为空
if (node.getRight() != null) {
// 右递归前序查找
res = preOrderSeach(node.getRight(), no);
}
// 如果不为空说明进行 “右递归前序查找” 时查找到了该节点
return res;
}
}程序运行结果如下所示:
1、2 中序遍历查找
前序遍历的查找思路:
(1)判断当前结点(假设A节点)的左子节点是否为空,如果不为空,则递归中序查找。
(2)如果当前节点(假设A节点)的左子节点的递归中序查找已经找到,则返回;如果没有找到,就和当前节点(假设A节点)比较,如果是则返回当前结点,否则判断当前节点(假设A节点)的右子节点是否为空。
(3)如果当前节点(假设A节点)的右子节点是不为空,则进行当前节点(假设A节点)的右子节点的递归中序查找;如果当前节点(假设A节点)的右子节点的递归中序查找已经找到,则返回;如果找完一整棵树还是没有找到,则返回 null。
我们这里也举个例子,也用图1的二叉树进行中序遍历查找,假设我要找的是序号为7的人物和序号为8的人物,这里我只写出序号为7的人物的查找思路,序号为8的人物的查找思路是和查找序号为7的人物的思路是一样的,有兴趣的读者可以自己分析一把序号为8的人物的查找思路,好,我们现在开始进行分析查找序号为7的人物的思路:
(1)一开始看到序号为1的根节点,发现根节点的左子节点不为空,然后就往根节点的左子节点(序号为2)进行中序遍历查找。
(2)发现序号为2的节点的左子节点不为空,又往序号为2的节点的左子节点(序号为4)进行中序遍历查找。
(3)发现序号为4的节点是叶子节点,那么就会拿该叶子节点的序号和要查找的节点的序号进行比较,4不等于7,于是序号为2的节点的左子节点的递归中序遍历已经结束。
(4)这时候拿序号为2的节点的序号和要查找的节点的序号进行比较,2不等于7,于是判断序号为2的节点右子节点是否为空,发现不为空,又进行序号为2的右子节点(序号为5)的递归中序遍历查找。
(5)发现序号为5的节点是叶子节点,那么就会拿序号为5的节点的序号和要查找的节点的序号进行比较,5不等于7,序号为2的节点的右子节点的递归中序遍历查找结束,根节点的左子节点(序号为2)递归中序遍历查找也跟着结束。
(6)这时候就拿根节点的序号和要查找的节点的序号进行比较,1不等于7,于是就判断根节点的右子节点是否为空,发现不为空,又进行根节点的右子节点(序号为3)的递归中序遍历查找。
(7)发现序号为3的节点的左子节点不为空,然后进行序号为3的节点的左子节点(序号为6)的递归中序遍历查找。
(8)发现序号为6的节点是叶子节点,于是拿该叶子节点的序号和要查找的节点的序号进行比较,6不等于7,这时候序号为3的节点的左子节点的递归中序遍历查找结束,然后又拿序号为3的节点的序号和要查找的节点的序号进行比较,3不等于7。
(9)这时候去判断序号为3的节点的右子节点是否为空,发现不为空,又进行序号为3的节点的右子节点(序号为7)的递归中序遍历查找。
(10)发现序号为7的节点是叶子节点,于是拿该叶子节点的序号和要查找的节点的序号进行比较,发现7等于7,立即返回该叶子节点,查找全过程结束。
好,对图1中的二叉树序号为7和序号为8的人物的中序遍历查找,我们也用代码实现一把:
(1)我们还是继续用上面前序遍历查找的节点类 FigureNode,这里我们只序号添加一个测试类 Test2 即可 :
public class Test2 {
private FigureNode root;
public static void main(String[] args) {
Test2 test = new Test2();
test.createBinaryTree();
test.infixOrderSearch(7);
System.out.println("*****************");
test.infixOrderSearch(8);
}
// 创建一棵二叉树
private void createBinaryTree() {
FigureNode figureNode = new FigureNode(1,"如来佛祖");
FigureNode figureNode2 = new FigureNode(2,"观音菩萨");
FigureNode figureNode3 = new FigureNode(3,"牛魔王");
FigureNode figureNode4 = new FigureNode(4,"孙悟空");
FigureNode figureNode5 = new FigureNode(5,"猪八戒");
FigureNode figureNode6 = new FigureNode(6,"红孩儿");
FigureNode figureNode7 = new FigureNode(7,"铁扇公主");
root = figureNode;//根节点的人物是如来佛祖
root.setLeft(figureNode2);//根节点的左子节点是序号为2的节点
root.setRight(figureNode3);//根节点的右子节点是序号为3的节点
figureNode2.setLeft(figureNode4);//序号为2的左子节点是序号为4的节点
figureNode2.setRight(figureNode5);//序号为2的右子节点是序号为5的节点
figureNode3.setLeft(figureNode6);//序号为3的左子节点是序号为6的节点
figureNode3.setRight(figureNode7);//序号为3的右子节点是序号为7的节点
}
// 中序遍历查找,以根节点为当前节点进行查找
private void infixOrderSearch(int no) {
if (root != null) {
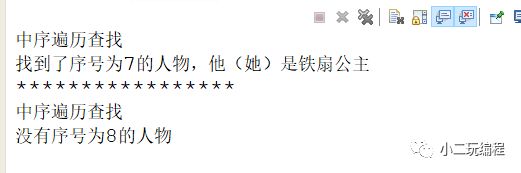
System.out.println("中序遍历查找");
FigureNode result = infixOrderSearch(root, no);
if (result == null) {
System.out.println("没有序号为" + no + "的人物");
} else {
System.out.println("找到了序号为" + no + "的人物,他(她)是"
+ result.getName());
}
} else {
System.out.println("这是一棵空的二叉树");
}
}
// 中序遍历查找
private FigureNode infixOrderSearch(FigureNode node, int no) {
FigureNode res = null;
// 判断当前节点的左子节点是否为空
if (node.getLeft() != null) {
// 左递归中序查找 找到节点 则返回
res = infixOrderSearch(node.getLeft(), no);
}
// 如果不为空说明进行 “左递归中序查找” 时查找到了该节点
if (res != null) {
return res;
}
if (node.getNo() == no) {// 比较当前节点
return node;
}
// 当前的结点的右子节点是否为空
if (node.getRight() != null) {
// 右递归中序查找
res = infixOrderSearch(node.getRight(), no);
}
// 如果不为空说明进行 “右递归中序查找” 时查找到了该节点
return res;
}
}程序运行结果如下所示:
1、3 后序遍历查找
前序遍历的查找思路:
(1)判断当前结点(假设A节点)的左子节点是否为空,如果不为空,则递归后序查找。
(2)如果递归后序遍历查找当前结点(假设A节点)的左子节点已经找到,就返回;如果递归后序遍历查找当前结点(假设A节点)的左子节点没有找到,那么就判断当前结点(假设A节点)的右子节点是否为空,如果不为空,则递归后序遍历查找当前结点(假设A节点)的右子节点,如果找到,就返回。
(3)如果递归后序遍历查找当前结点(假设A节点)的右子节点还是没有找到,就和当前节点进行比较,如果找到则返回;如果后序遍历查找完一棵二叉树还是没有找到,则返回 null。
好,我们也举个例子,用图1的二叉树进行后序遍历查找,假设我要找的是序号为6的人物和序号为8的人物,序号为8的人物查找思路我就不写了,我只写序号为6的后序遍历查找思路;
(1)一开始我们看到的是根节点(序号为1),先判断根节点的左子节点是否为空,发现不为空,于是进行根节点的左子节点(序号为2)的递归后序遍历查找。
(2)然后又判断序号为2的节点的左子节点是否为空,发现不为空,又进行序号为2的节点的左子节点(序号为4)的递归后序遍历查找。
(3)发现序号为4的节点是叶子节点,于是拿该叶子节点的序号和要查找的节点的序号做比较,4不等于6,这时候序号为2的节点的左子节点的递归后序遍历查找结束。
(4)判断序号为2的节点的右子节点是否为空,发现不为空,于是进行序号为2的节点的右子节点(序号为5)的递归后序遍历查找。
(5)发现序号为5的节点是叶子节点,于是拿该叶子节点的序号和要查找的节点的序号进行比较,5不等于6。
(6)这时候序号为2的节点的右子节点的递归后序遍历查找已经结束,于是拿序号为2的节点的序号和要查找的节点的序号进行比较,2不等于6。
(7)也这个时候根节点的左子节点的递归后序遍历查找已经结束,又判断根节点的右子节点是否为空,发现不为空,于是进行根节点的右子节点(序号为3)的递归后序遍历查找。
(8)判断序号为3的左子节点是否为空,发现不为空,于是进行序号为3的节点的左子节点(序号为6)的递归后序遍历查找。
(9)发现序号为6的节点是叶子节点,于是拿该叶子节点的序号和要查找的序号进行比较,7等于7,于是返回该叶子节点,结束全程递归后序查找。
好了,对图1中的二叉树序号为6和序号为8的人物的后序遍历查找,我们也还是用代码实现一把:
(1)我们还是继续用上面前序遍历查找的节点类 FigureNode,这里我们只序号添加一个测试类 Test3 即可 :
public class Test3 {
private FigureNode root;
public static void main(String[] args) {
Test3 test = new Test3();
test.createBinaryTree();
test.postOrderSearch(6);
System.out.println("*****************");
test.postOrderSearch(8);
}
// 创建一棵二叉树
private void createBinaryTree() {
FigureNode figureNode = new FigureNode(1, "如来佛祖");
FigureNode figureNode2 = new FigureNode(2, "观音菩萨");
FigureNode figureNode3 = new FigureNode(3, "牛魔王");
FigureNode figureNode4 = new FigureNode(4, "孙悟空");
FigureNode figureNode5 = new FigureNode(5, "猪八戒");
FigureNode figureNode6 = new FigureNode(6, "红孩儿");
FigureNode figureNode7 = new FigureNode(7, "铁扇公主");
root = figureNode;// 根节点的人物是如来佛祖
root.setLeft(figureNode2);// 根节点的左子节点是序号为2的节点
root.setRight(figureNode3);// 根节点的右子节点是序号为3的节点
figureNode2.setLeft(figureNode4);// 序号为2的左子节点是序号为4的节点
figureNode2.setRight(figureNode5);// 序号为2的右子节点是序号为5的节点
figureNode3.setLeft(figureNode6);// 序号为3的左子节点是序号为6的节点
figureNode3.setRight(figureNode7);// 序号为3的右子节点是序号为7的节点
}
// 后序遍历查找,以根节点为当前节点进行查找
private void postOrderSearch(int no) {
if (root != null) {
System.out.println("后序遍历查找");
FigureNode result = postOrderSearch(root, no);
if (result == null) {
System.out.println("没有序号为" + no + "的人物");
} else {
System.out.println("找到了序号为" + no + "的人物,他(她)是"
+ result.getName());
}
} else {
System.out.println("这是一棵空的二叉树");
}
}
// 后序遍历查找
private FigureNode postOrderSearch(FigureNode node, int no) {
FigureNode res = null;
// 判断当前节点的左子节点是否为空
if (node.getLeft() != null) {
// 左递归后序查找 找到节点 则返回
res = postOrderSearch(node.getLeft(), no);
}
// 如果不为空说明进行 “左递归后序查找” 时查找到了该节点
if (res != null) {
return res;
}
// 当前的结点的右子节点是否为空
if (node.getRight() != null) {
// 右递归后序查找
res = postOrderSearch(node.getRight(), no);
}
// 如果不为空说明进行 “右递归后序查找” 时查找到了该节点
if (res != null) {
return res;
}
if (node.getNo() == no) {// 比较当前节点
return node;
}
return res;
}
}程序运行结果如下所示:
小结:从目前来看后序遍历查找所用的比较次数是最少的,推荐使用后序遍历查找,有兴趣的读者可以试验一把。