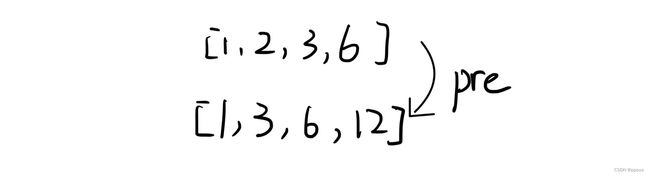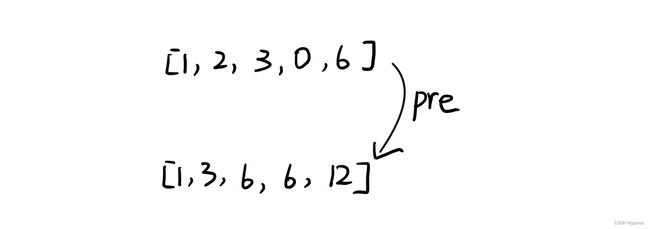【前缀和】560.和为 K 的子数组

Halo，这里是Ppeua。平时主要更新C++，数据结构算法，Linux与ROS…感兴趣就关注我bua！

题目:

示例:

题解：

解法一:

暴力解法:我们很容易想到通过两个for循环去遍历数组中所有和的可能,之后来判断有几个满足K.他的代码十分的简单,所以这里直接给出.

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.size(); ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
};

这里通过一个start与end来控制子数组区间.若为K则计数++.

我们仔细观察这样的做法.可以很容易的发现,**我们可以通过前缀和来解决两层循环的问题.**于是就有了解法二:利用前缀和来解决此类问题.

解法二:

不熟悉前缀和的uu们可以看看这篇文章:[前缀和]((138条消息) 【高精度加减乘除法、一维二维前缀和&&差分】思路讲解及代码实现_ppeua的博客-CSDN博客)

这里就直接开始推导了,这里利用的是一维的前缀和方法.

定义:**pre[i]**表示从0~i的所有数组元素之和.

那么根据前缀和的定义:j~i区间内的元素之和可以表示为:pre[i]-pre[j-1],我们要判断的就是这个结果能不能等于K.

所以现在的求解就简化为下面这个式子:

我们对两边式子进行简单的数学推导可以得到.

这样我们可以通过一个hash来存储值,之后只要验证当前遍历的这个前缀和-k的结果是否出现在hash当中.若出现则+上其出现的次数.

代码较为简单:

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
       for(int i=1;i<nums.size();i++)
       {
        nums[i]+=nums[i-1];
       }
       unordered_map<int,int>mp;
       mp[0]=1;
       int res=0;

       for(int i=0;i<nums.size();i++)
       {
        
        if(mp.find(nums[i]-k)!=mp.end())
        {
            res+=mp[nums[i]-k];
        }
        mp[nums[i]]++;
       }
       return res;
    }
};

有两个很重点的问题:

1. 为什么mp[0]=1?

   为了应对 nums[0] +nums[1] + … + nums[i] == k,也就是从下标 0 累加到下标 i刚好满足的情况.

   举个例子:k为6

   

​ 当这种情况下,第一次遍历到原数组为3,前缀和数组为6的位置的时候.此时pre-k=0,是刚好满足情况的.所以需要先预设一个mp[0]=1的情况.

2. 为什么是res+=mp[nums[i]-k]:

   举个例子:K仍为6

​

​ 这道题的答案是4,当遍历到第一个6的位置上时,得到第一个答案.遍历到第二个位置时,得到第二个答案.这两种情况都是:pre-k=0

遍历到12时得到第三个答案,此时pre-k=6.那么此时只有三个答案嘛?不是的,12-第一个6是一个答案.12-第二个6也是一个答案.

遍历到第二个位置时,得到第二个答案.这两种情况都是:pre-k=0

遍历到12时得到第三个答案,此时pre-k=6.那么此时只有三个答案嘛?不是的,12-第一个6是一个答案.12-第二个6也是一个答案.

所以:res+=mp[nums[i]-k],是为了直接加上相同情况的可能.