图解LeetCode——剑指 Offer 07. 重建二叉树
一、题目
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
二、示例
2.1>示例 1:
【输入】preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
【输出】[3,9,20,null,null,15,7]
2.2> 示例 2:
【输入】preorder = [-1], inorder = [-1]
【输出】 [-1]
限制:
0<= 节点个数 <=5000
三、解题思路
根据题目描述,我们需要通过题目给出的一棵树的前序遍历和中序遍历,来重建这棵二叉树。那么首先我们需要知道这两种遍历的方式是怎么样的:
【前序遍历】首先访问
根结点,然后遍历左子树,最后遍历右子树。
【中序遍历】首先遍历左子树,然后访问根节点,最后遍历右子树。
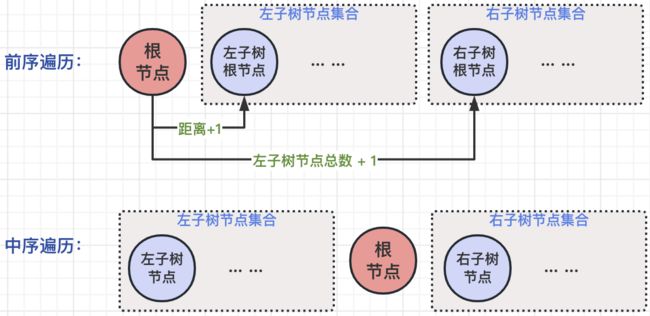
那么,我们首先需要做的就是,通过前序遍历和后序遍历的遍历方式,来找到最近两层节点的关系,即:node、node.left和node.right;如下图所示,假设根节点所在前序遍历数组preorder的下标为:index,根据前序遍历规则我们可以得出如下结论:
【子树根节点所在
preorder数组中的位置】index
【左子树根节点所在preorder数组中的位置】index + 1
【右子树根节点所在preorder数组中的位置】index + 左子树节点总和 + 1
而我们怎么获得左子树节点总和呢?这时候,我们就可以根据中序遍历规则来计算出来了,我们假设某一个子树中序遍历数组为inorder,那么根节点所在位置是pos,某子树范围在[start, end]之间,那么就可以得出如下结论:
【左子树节点总和】pos - start
主要逻辑说完了,由于我们可以根据中序遍历+子树根节点位置划分左子树节点集合与右子树节点集合,那么通过递归调用就可以重塑这棵二叉树了。
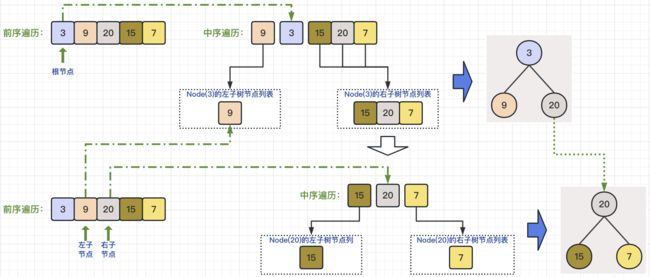
解题思路说完了,我们还是举例来看一下重塑二叉树的过程。输入preorder = [3,9,20,15,7], inorder = [9,3,15,20,7],请参数如下图中的图解所示,看一下具体的处理过程:
四、代码实现
public class Solution {
int[] preorder;
HashMap mark;
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder == null || inorder == null) return null;
this.preorder = preorder;
mark = new HashMap();
for(int i = 0; i < inorder.length; i++)
mark.put(inorder[i], i);
return childNode(0, 0, inorder.length-1);
}
public TreeNode childNode(int root, int start, int end) {
if (start > end) return null;
TreeNode node = new TreeNode(preorder[root]);
// 【子树根节点位置】index
int index = mark.get(preorder[root]);
// 【右子树根节点位置】index + 1
node.left = childNode(root+1, start, index-1);
// 【左子树根节点位置】index + 左子树长度(index-start)+ 1
node.right = childNode(root+index-start+1, index+1, end);
return node;
}
} 今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」