数据结构---树和二叉树
这里写目录标题
- 树和二叉树的定义
-
- 树的定义
- 树的基本术语
- 线性结构和树形结构的比较
- 二叉树的定义
-
- 起因
- 定义
- 案例引入
-
- 前缀码编码
- 表达式的实现
- 二叉树的抽象类型定义
- 二叉树的性质和存储结构
-
- 二叉树的性质
- 二叉树的特殊形式
-
- 满二叉树
- 完全二叉树
- 完全二叉树的两个性质
- 二叉树的存储结构
-
- 顺序存储结构
- 链式存储结构
- 遍历二叉树
-
- 简介
- 先序
- 中序
- 后序
- 一级目录
-
- 二级目录
- 二级目录
- 二级目录
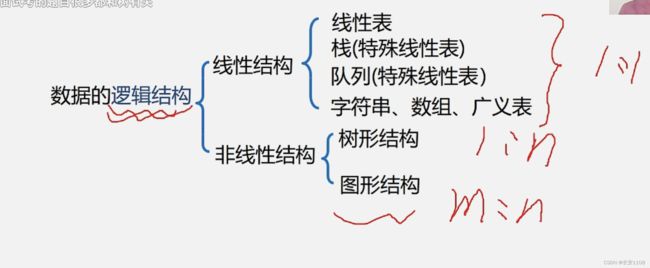
树和二叉树的定义
树的定义
,图中树的深度是四层
孩子:结点子树的根结点
双亲:与孩子反过来
例如:B是A的孩子;A是B的双亲
子孙:某节点子树中的任一个结点
祖先:从根到该结点所“途径"的"所有“结点,例如,H的祖先是A、D

一棵树也是森林,把一棵树的根结点去掉,就变成了三棵树,就是一个普通的森林,
森林加上一个双亲结点,就变成了一颗树
线性结构和树形结构的比较
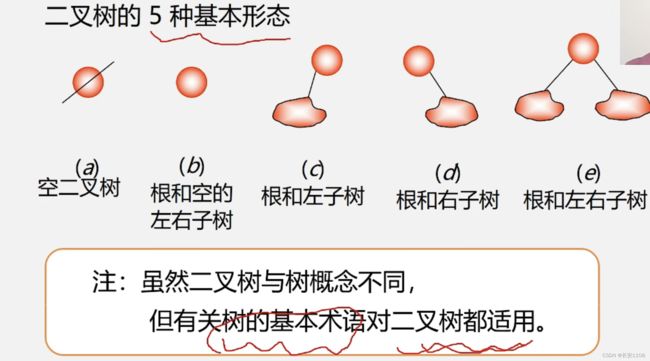
二叉树的定义
起因
定义

注意 子树有左右之分,并且次序不能颠倒,根可以有空的左右子树
注意
二叉树:哪怕其中一个子树是空的 那么另一个子树也得在自己位置 并且区分左右
树:不区分左右,其中一个子树为空时,另一个只有一个位置
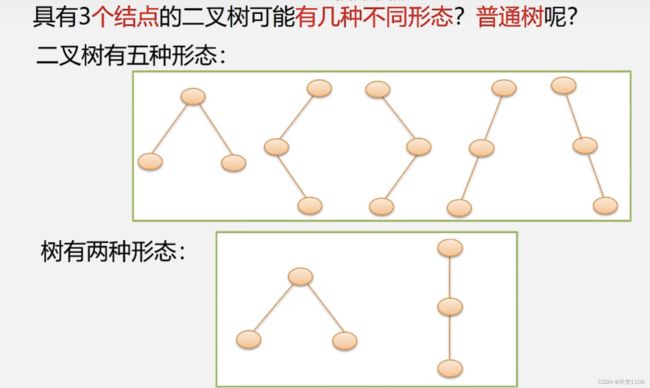
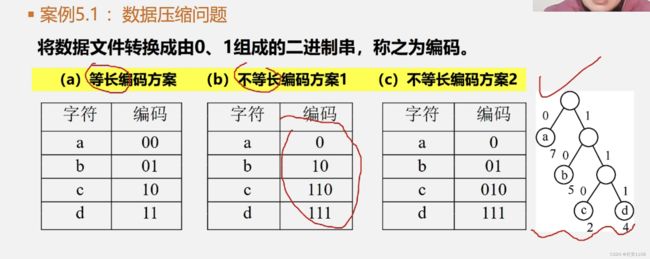
案例引入
前缀码编码
表达式的实现
二叉树的抽象类型定义


创建二叉树时,根据definition来构造 而definition的值分别对应着三个不同的遍历方式
二叉树的性质和存储结构
二叉树的性质

直接假设二叉树是满二叉树 也就是直接计算最多情况下的结点数,就是“至多”的结点数
第i层 那就是求等比数列的常数项 也就是a1*(q的n-1次方) a1是1

每层至少一个
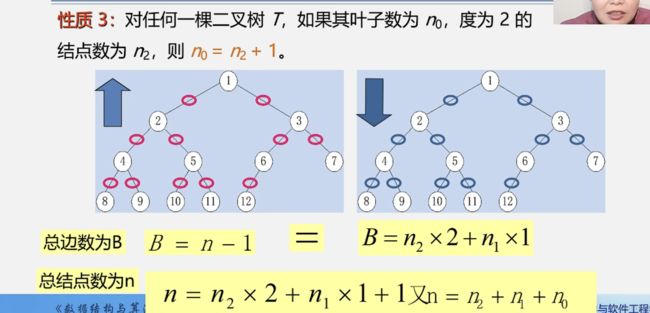
证明:1.以总边数为桥梁
2.从下往上分析:每个结点头上都连着一个边,只有根结点没有,所以 总边数B=n-1(n是总结点数)
3.从上往下分析:B=2n2+1n1
(n2、n1、分别表示度为2和度为1的结点数)
4.以B为桥梁 带入n=n2+n1+n0
二叉树的特殊形式
满二叉树


满二叉树 必须每个位置都有结点 每层都要满 叶子结点必须都在最后一层
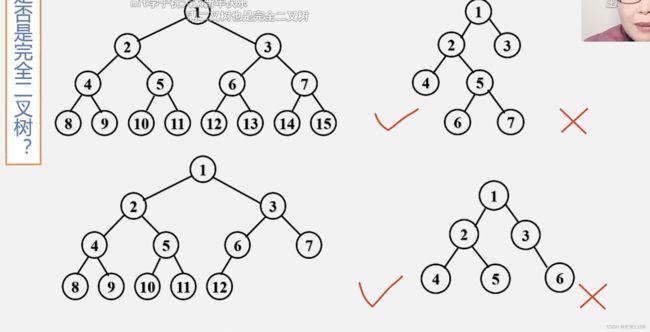
完全二叉树
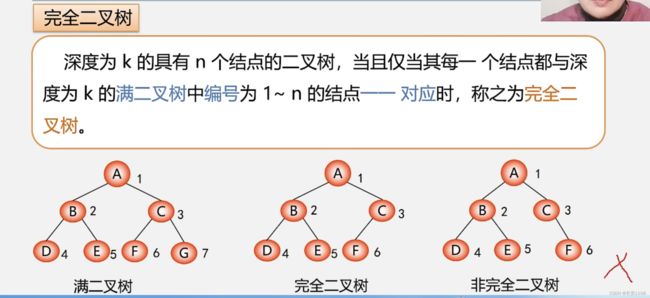
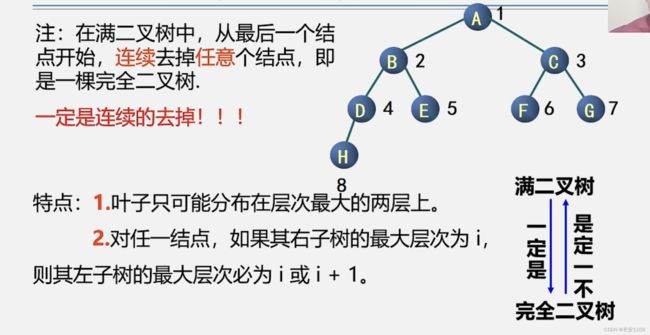
要从满二叉树中连续的去掉元素而不修改 也就是编号位置不能变 结点中存放的元素也不能变 就是将完全二叉树映射到满二叉树时 没有异常的地方 可以残缺 但不可以异常 并且 一定要从左往右是连续的 不能有缺口
完全二叉树的两个性质
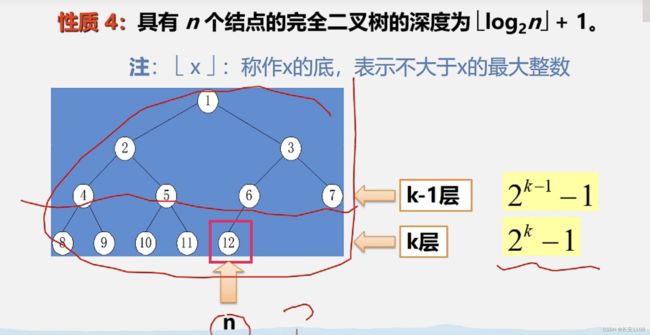
因为是完全二叉树 去掉最后一层 就是满二叉树 补全最后一层 也是满二叉树 所以 可以利用满二叉树的性质来构造一个不等式,
去掉最后一层 就是满二叉树 那么不等式左边就是k-1层时的总结点数
补全最后一层 就是满二叉树 那么不等式右边就是k层时的总结点数
之后简化不等式 最后一步将小于号改成去小于x的最大整数

因为是完全二叉树 去掉最后一层 就是满二叉树 补全最后一层 也是满二叉树 所以 可以利用满二叉树的性质来构造一个不等式,之后简化不等式 最后一步将小于号改成去小于x的最大整数
总结来说 除了根结点
其他结点:双亲结点的编号是【i/2】
左孩子结点是2i
右孩子结点是2i+1
如果左右孩子的编号超出了最大结点数 那么就是孩子不存在
二叉树的存储结构
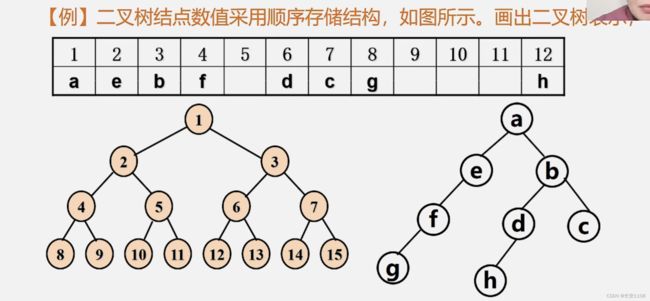
顺序存储结构
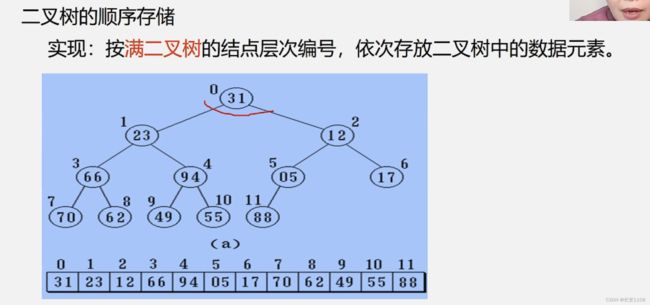
按照满二叉树的位置定义编号 再定义一个数组 编号对应数组下标

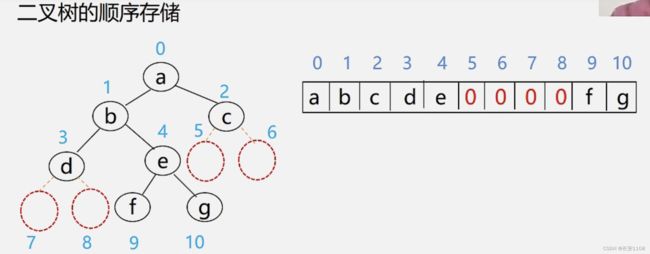
空值 数组位置不能缩进 仍然保留 数值为空
所以就造成了空间的浪费

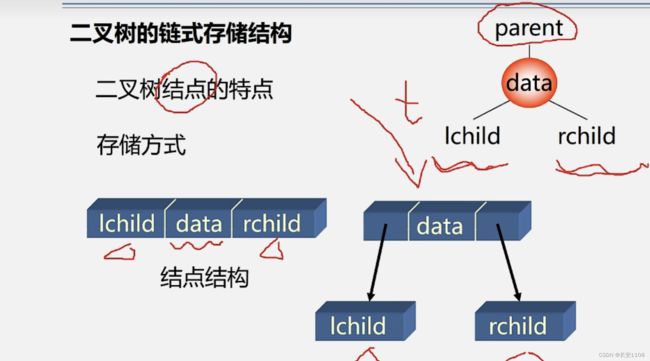
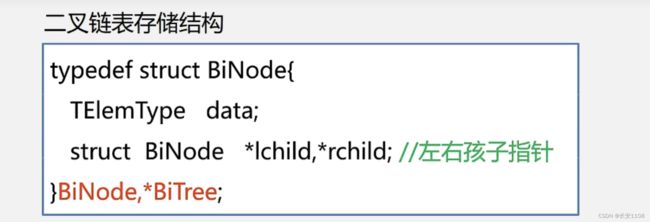
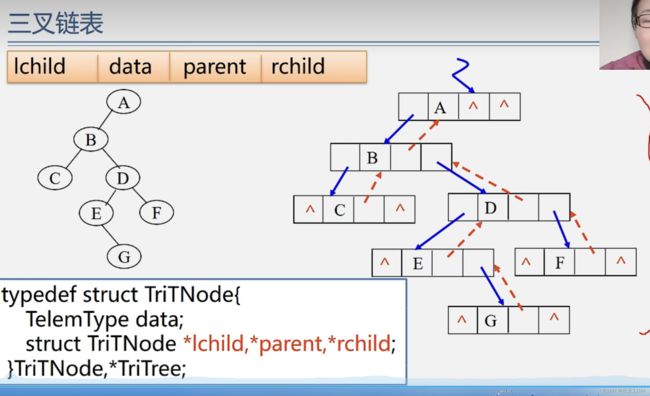
链式存储结构


除了根节点 其他结点一定有双亲 那么每个双亲肯定会牺牲一个链域来存放孩子的地址 所以 空指针数目是2n-(n-1)
遍历二叉树
简介


遍历每一个子树时 将子树也按照整棵树的遍历方式遍历 ,也就是以根结点为参考 转换根结点的参考
先序

先以整个树为参考 先访问根结点
之后访问左子树:这时将左子树的B 看成根结点 继续采用先序的访问方式来访问B的左子树 依次类推 直到访问到左右子树为空的叶子结点 从而完成对左子树的访问
最后访问右子树:这时将右子树中的D看成根结点 继续采用先序的访问方式来访问D的左子树 依次类推递归 直到访问到左右子树为空的叶子结点 从而完成对右子树的访问
中序
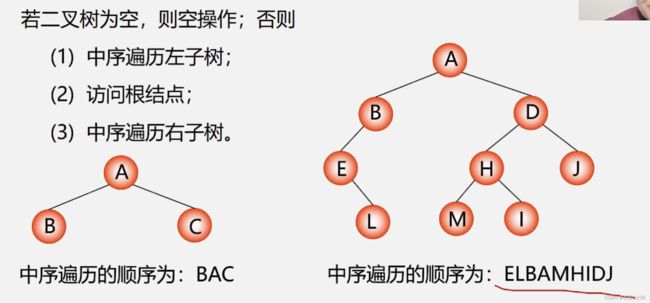
先访问左子树:这时将左子树的B 看成根结点 继续采用先序的访问方式来访问B的左子树 依次类推 直到访问到左右子树为空的叶子结点 从而完成对左子树的访问
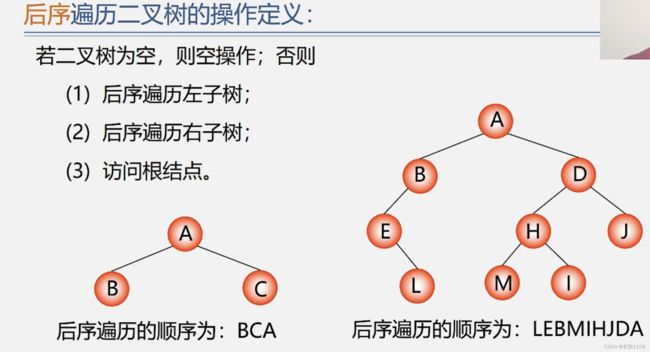
后序
案例