数据挖掘项目:金融银行风控信用评分卡模型(上篇)
数据来自Kaggle的Give Me Some Credit,有15万条的样本数据,网上的分析说明有很多,本人结合其他大佬的方法,对数据进行细致的分析,主要分析在EDA环节,之后尝试使用toad这个评分卡的库,以及使用quct结合卡方检验分箱的方法,使用AUC和KS,结合交叉验证对比分析哪个效果更好。
目录
由于整篇文章的篇幅过长,因此分为上下两部分。
- 上篇
- 理解数据
- 探索性数据分析
- 数据预处理
- 特征工程
- 下篇
- 使用toad进行woe分箱,并进行模型评估
- 手写卡方分箱,并进行模型评估
- 评分卡建立
1.1背景介绍
银行领域评分卡一般分为四种,A、B、C、F卡:
A卡表示为贷前评分卡。
B卡表示为贷中评分卡。
C卡表示为贷后评分卡。
F卡表示为反欺诈评分卡。
1.2基本的项目流程
典型的信用评分模型主要的开发流程如下所示:
(1)数据获取,包括获取存量客户及潜在客户的数据。存量客户是指已经在证劵公司开展相关融资业务的客户,包括个人客户和机构客户;潜在客户是指
(2)数据预处理,主要工作包括数据清洗,缺失值处理,异常值处理,主要是为了将获取的原始数据转化为可用作模型开发的数据。
(3)EDA探索性数据分析,该步骤主要是获取样本总体的大概情况,描述样本总体情况的指标主要有直方图和箱线图等等。
(4)变量选择,主要是通过统计学的方法,筛选出对违约状态影响最显著的指标。常见的特征筛选方法,一般分为三种:过滤法、嵌入法、包装法。过滤法一般采用sklearn当中的方差过滤和卡方过滤。嵌入法是一种让算法自己决定使用哪些特征的方法。包装法和嵌入法很像,但包装法需要使用一个目标函数作为黑盒来帮助选择特征。一般来说对于评分卡模型,还会使用woe值和IV值筛选特征。
(5)模型开发,该步骤主要包括变量分段、变量的WOE(证据权重)变换和逻辑回归估算三部分。
(6)模型评估,一般评分卡中常用的评估方法,有Accuracy计算准确性、画出ROC曲线、计算AUC数值、还有KS值、最后做一个交叉验证看模型的稳定性。
(7)最后一步就是形成评分卡
2.1数据获取
## 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression as LR ##调用sklearn逻辑回归
from imblearn.over_sampling import SMOTE ## 处理数据不平衡问题
import seaborn as sns
# 画图显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = Falsedata = pd.read_csv(r"rankingcard.csv",index_col = 0) ##首先导入训练集数据
test = pd.read_csv(r"cs-test.csv",index_col = 0) ##导入测试集数据2.2探索数据
#观察数据类型
data.head()## 查看训练集数据
test.head()# 观察数据维度
print(data.shape)
print(test.shape)
(150000, 11)
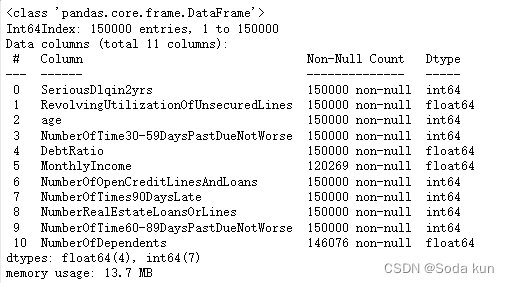
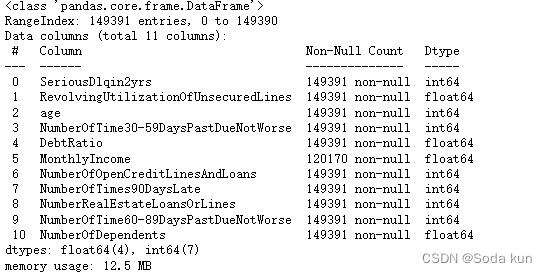
(101503, 11)data.info() ##查看里面的基本情况,字符类型以及缺失值情况下面可以看到数据的大致情况。数据属于个人消费类贷款,只考虑信用评分最终实施能够使用到的数据应从如下一些方面获取数据:
基本属性:包括借款人当时的年龄。
偿债能力:包括了借款人的月收入、负债比率。
信用往来:两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90天或以上的逾期次数
财产状况:包括了开放式信贷和贷款数量、不动产贷款或额度数量
贷款属性:暂无
其他因素:包括了借款人的家属数量(不包括本人在内)
时间窗口:自变量的观察窗口为过去两年,因变量表现窗口为未来两年。
标签如下所示:
SeriousDlqin2yrs:指在过去两年中至少有一次逾期90天或更长时间的信用违约情况。是本数据集的目标变量。
RevolvingUtilizationOfUnsecuredLines:指信用卡和个人信贷余额与可用信贷额度之比。
age:指借款人的年龄。
NumberOfTime30-59DaysPastDueNotWorse:指在过去两年中出现了30-59天的逾期但没有更严重的逾期情况的次数。
DebtRatio:指负债比率,即每月债务支付、赡养费用和生活费用除以每月总收入。
MonthlyIncome:指借款人的月收入。
NumberOfOpenCreditLinesAndLoans:指借款人未偿还的信用额度。
NumberOfTimes90DaysLate:指在过去两年中出现了90天或更长时间的逾期情况的次数。
NumberRealEstateLoansOrLines:指不包括家庭住房在内的房地产贷款和额外的抵押贷款次数。
NumberOfTime60-89DaysPastDueNotWorse:指在过去两年中出现了60-89天的逾期但没有更严重的逾期情况的次数。
NumberOfDependents:指借款人在家庭中需要抚养的家属人数。
##去除重复值,注意去除的是重复的行,因为对于150000行的数据,
##存在两组完全一样的数据几乎不太可能,有可能是录入错误
data.drop_duplicates(inplace = True) ##删除重复值,并且替换
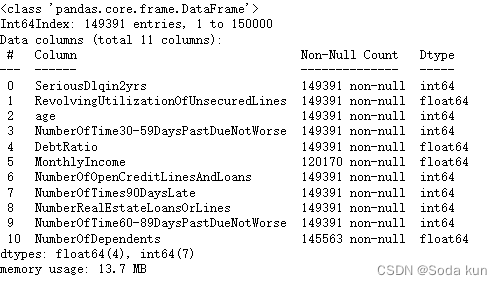
data.info()##删除后一定要记得恢复索引!
data.index = range(data.shape[0])2.3 EDA 探索性数据分析
2.3.1 缺失值分析
##探索一下模型的缺失值
data.isnull().sum() ##用isnull语句+sum语句,返回布尔值相加,得到每列缺失值的数目data.isnull().sum()/len(data) ##判断每一列缺失值所占的比值2.3.2 数据平衡性
## 画饼图
figure,ax = plt.subplots(figsize = (12,4))
data.SeriousDlqin2yrs.value_counts().plot.pie(autopct = '%1.1f%%')正样本(好客户)占比93.3%,负样本(坏客户)占比6.7%。
说明客户一般为好客户。我们需要捕捉的是坏客户,但由于比例太过悬殊,此时样本不平衡,需要后续进行处理。
2.3.3 异常值分析
通过对数据进行分析,发现有很多和业务理解不相同的数据。
同时根据前面训练集和测试集的对比,可以发现在测试集当中同样存在这样的异常值,所以对这样的所谓异常值不能简单的剔除。
如果是实际工作当中出现这样的问题,需要和业务人员进行确认,如果在比赛中遇到,那就要做好分箱,结合业务和woe进行分析。
信用卡和个人信贷余额与可用信贷额度之比-RevolvingUtilizationOfUnsecuredLines
fig = plt.figure(figsize = (14,4))
ax1 = fig.add_subplot(1,2,1)
sns.distplot(data['RevolvingUtilizationOfUnsecuredLines'],kde = True) ##画出直方图
ax1 = fig.add_subplot(1,2,2)
sns.boxplot(y=data['RevolvingUtilizationOfUnsecuredLines']) ## 画出箱线图
plt.show()我的理解是,正常情况下信用卡和个人信贷余额与可用信贷额度之比的取值范围应该是[0,1]。
而这些异常数据有可能是没有除以总额度造成的,或者是其他情况,需要借助具体的业务进行分析。
一般认为贷款额度与总额度比例小于1是合理的情况。因此先分析比例小于时,贷款额度与总额度比例和好坏客户之间的关系。
这里需要自己定义个函数get_compare_plot,可以画出不同自定义分箱的bardete图像,如果对定义函数有疑问可以大家一起探讨。
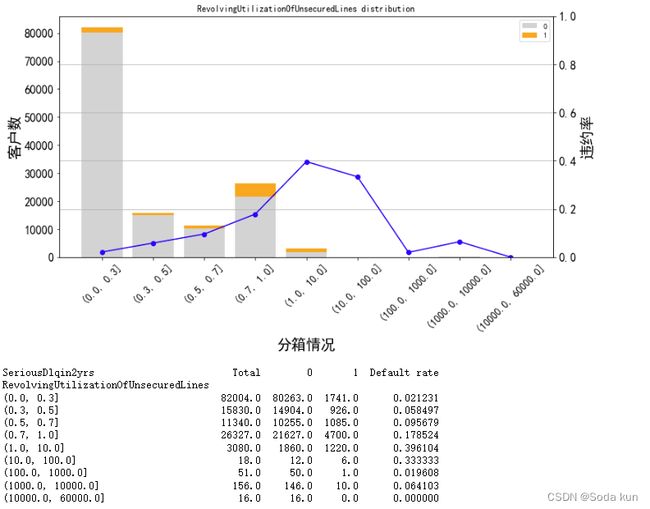
cut_num = [0,0.3,0.5,0.7,1,10,100,1000,10000,60000]
get_compare_plot(data,feature_plot = 'RevolvingUtilizationOfUnsecuredLines',cut_num=cut_num,is_qcut=False)这里可以看到,当Revol(贷款额度与总额度比例) 小于1时,随着该比例的增加,客户违约率也在增加,符合业务逻辑。
正常来说,应该是随着比例的增加,客户违约率也会增加,但是在大于10后,该规律发生了改变,
并且可以通过客户数可以发现数据大于10的客户数突然要小了很多,因此对其进行进一步分析。
如果要提高模型预测的准确性,可以这里对测试集中Revol特征的客户数进行对比,因为篇幅的原因这里不作过多的展示。
对[1,10]之间进行分析,找到下滑最好的一个分割点。
cut_num=[]
for i in np.arange(-1,10,1):
cut_num.append(i)
get_compare_plot(data,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)对1-10分析后,可以看到,从1-2开始违约率是在逐渐下降的,这不符合正常的规律性,应该是Revol越大,违约率越大。
而且发现在1-2时,样本个数比之后都大很多,之后违约率有了特别大的提升,大概率是因为样本数变少,具有随机性。
所以对[1,2]之间的数据进行细分。
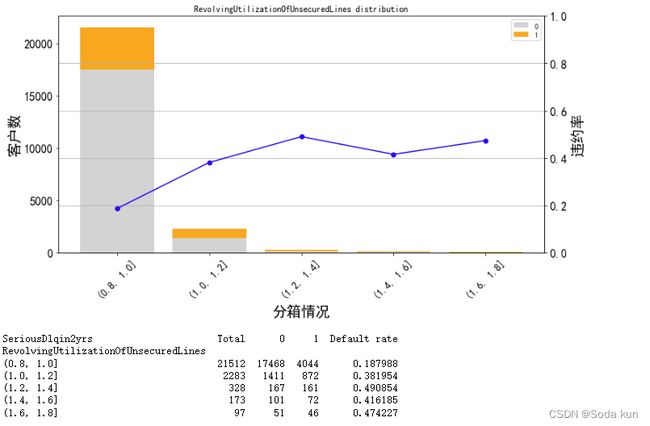
cut_num=[]
for i in np.arange(0.8,2,0.2):
cut_num.append(i)
get_compare_plot(data,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)之间对0-2之间做过分析,因此从0.8开始。可以发现数据走势差不多。
通过和之前的分析对比来看,Revol在0~2内,违约率增加。超过2之后,客户数量迅速下降和违约率也有降低的趋势。因此,可以认为Revol=2,
是我们要找的阈值。大于2的为异常值,小于2的为正常值。
print("贷款以及信用卡可用额度与总额度比例大于2的比重为:",100*(data['RevolvingUtilizationOfUnsecuredLines']>2).sum()/len(data),"%")
贷款以及信用卡可用额度与总额度比例大于2的比重为: 0.24834160023026822 %。
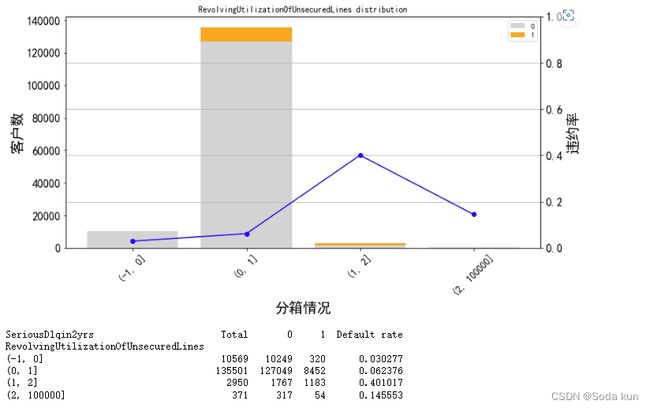
最终自己针对Revol的一个分箱结果如下,为之后的toad分箱和手动分箱都提供一个参考。
cut_num=[-1,0,1,2,100000]
get_compare_plot(data,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)以上是对Revol这个特征的一个比较全面的分析,通过不断分组探索数据的阈值,找出比较适合的切分点。
这里最后的数据处理,仍然存在问题,即可能会引入数据噪声,因为不清楚总额度具体值为多少。
以下的特征依旧会这么处理,分析数据的合理性,找出阈值,寻找异常值进行记录,后续处理的时候可进行删除等操作。
年龄-age分析
fig = plt.figure(figsize = (14,4))
ax1 = fig.add_subplot(1,2,1)
sns.distplot(data['age'],kde=True)
ax1 = fig.add_subplot(1,2,2)
sns.boxplot(y=data['age'])
plt.show()这里年龄的分布比较接近正态分布,通过对比训练集和测试集可以发现训练集中年龄有等于0的情况,而测试集里是从21开始。据我了解,银行能贷款的最低年龄为18岁,而年龄为0这个情况几乎不符合实际情况,所以后续处理的时候进行删除。
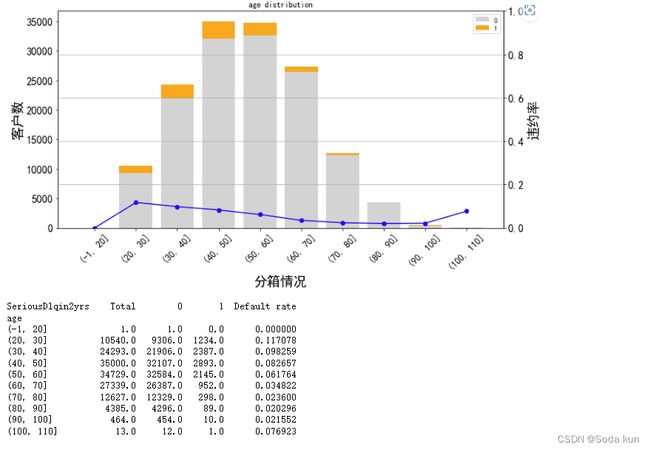
cut_num=[-1,20,30,40,50,60,70,80,90,100,110]
get_compare_plot(data,feature_plot="age",cut_num=cut_num,is_qcut=False)把年龄从-1-110每10岁分一组。发现随着年龄的增加,客户违约率在逐渐降低。
1.(年龄越大,越不容易违约)但在100-110这个阶段,违约率上升,因为样本数突然减少,可以看出违约人数也就1个人。
2.将年龄大于100的和90一起变成20人一箱。
3.因为测试集中也没有0岁的,所以将0岁的异常值删除(在后续删除)。
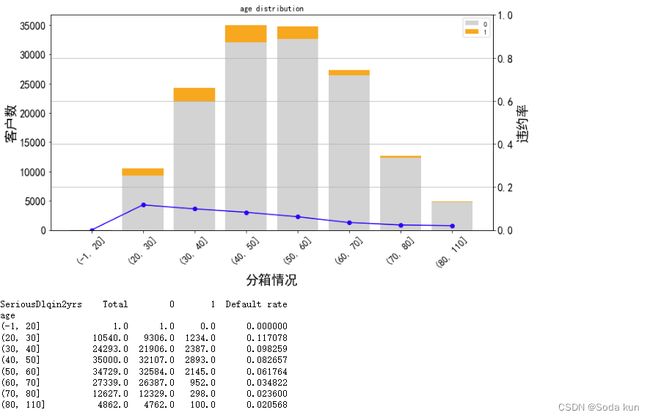
年龄最终分箱情况
cut_num=[-1,20,30,40,50,60,70,80,110]
get_compare_plot(data,feature_plot="age",cut_num=cut_num,is_qcut=False)过去两年内出现35-59天|60-89天|90天以上|逾期但是没有发展得更坏的次数
这里找出在限定范围内(两年内2*365),每种情况出现的最多次数。
- 30~59天24次。
- 60~89天最多的违规次数为12次。
- 90天以上最多的违规次数为8次。
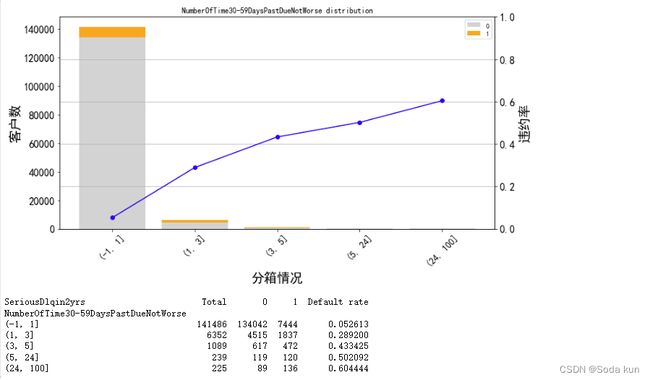
针对30-59天进行分箱分析
cut_num=[-1,1,3,5,24,100] ##因为5-24之间的人数很少,所以直接分成一箱
get_compare_plot(data,feature_plot="NumberOfTime30-59DaysPastDueNotWorse",cut_num=cut_num,is_qcut=False)可以看出,大于24次的人数只有225,针对这些人数可以进行删除,对150000的样本不会有太大影响。逾期的次数越多,客户违约率就越高,符合正常逻辑。
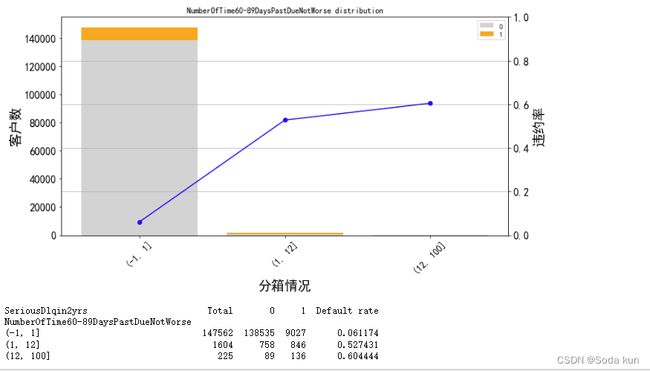
针对60-89天进行分箱分析
cut_num=[-1,1,12,100] ##因为1-12人数较少,所以分成一箱
get_compare_plot(data,feature_plot="NumberOfTime60-89DaysPastDueNotWorse",cut_num=cut_num,is_qcut=False)感觉像是同一批人。逾期的次数越多,客户违约率就越高,符合正常逻辑。
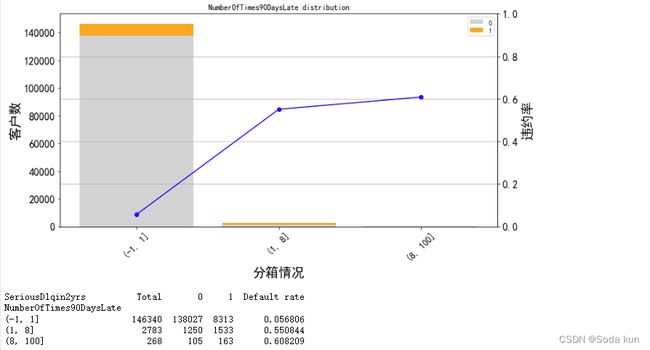
针对大于90天数据进行分析
cut_num=[-1,1,8,100]
get_compare_plot(data,feature_plot="NumberOfTimes90DaysLate",cut_num=cut_num,is_qcut=False)逾期的次数越多,客户违约率就越高,都符合正常逻辑。
负债率-DebtRatio
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(data['DebtRatio'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=data['DebtRatio'])
plt.show()负债率主要集中在“0附近”,正常来说,负债率应该是小于1的。但却有很多的值大于1,甚至上万,即存在异常值。
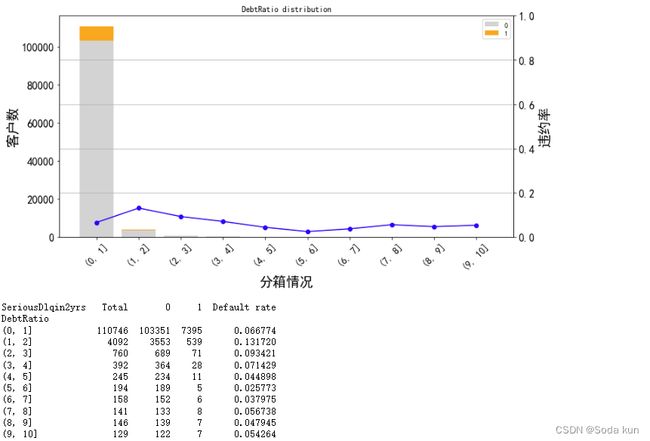
cut_num=[-1,0,0.3,0.5,0.7,1,10,100,1000,1000000]
get_compare_plot(data,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)负债率在0-1之间,随着负债率的增加,违约率也在增加。其中1达到最大0.11
当负债率为0时,有着较高的违约率,这点需要从业务上去理解。可能是因为若无负债(每月偿还债务,赡养费,生活费用除以月总收入),比较不靠谱。
当负债率达到10时,随着负债率的增加,违约率无显著的变化规律。这里对大于10继续进行分析。
cut_num=[10,100,1000,100000]
get_compare_plot(data,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)可以发现,在10以后违约率很低,只有0.05左右。
cut_num=[]
for i in np.arange(0,11,1):
cut_num.append(i)
get_compare_plot(data,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)针对0.10中进行分箱,可以发现相比0,1箱其他客户数都很小了,而且从2开始违约率和客户数都变小。所以阈值暂认为是2。
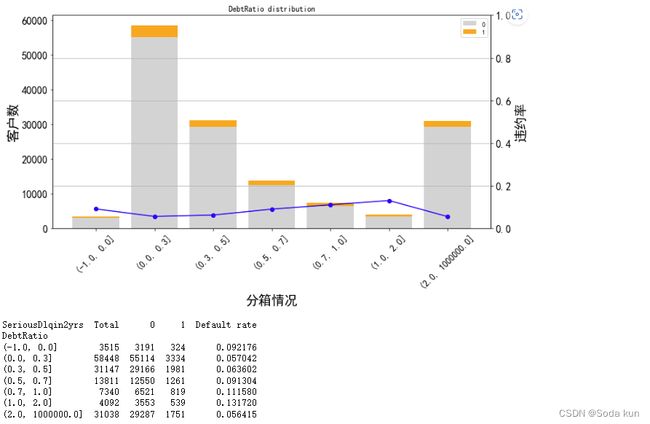
最终针对负债率的分析结果如下:
cut_num=[-1,0,0.3,0.5,0.7,1,2,1000000]
get_compare_plot(data,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)从这里可以看出,最后一箱随着负债率的提升,而负债率却下降,所以这里我猜测有可能是因为取数的时候,某些数据没有做除法。
月薪- MonthlyIncome
a=data['MonthlyIncome'].isnull().sum()/len(data)*100
print('月薪缺失值比例为%.2f%%'%(a))月薪缺失值比例为19.56%
对于缺失大于15%的数据连续性数据可以尝试使用随机森林进行填充。
cut_num=[0,1000,5000,10000,15000,20000,100000,1000000,10000000]
get_compare_plot(data,feature_plot="MonthlyIncome",cut_num=cut_num,is_qcut=False)对于月薪来说,一般会认为月薪越多,其违约率越小。但是因为月薪的数据跨度太大,所以之后结合toad再进行仔细分析。
开放式贷款和信贷数量-NumberOfOpenCreditLinesAndLoans
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(data['NumberOfOpenCreditLinesAndLoans'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=data['NumberOfOpenCreditLinesAndLoans'])
plt.show()通过直方图可以发现数据基本符合正态分布,并且数据存在一些异常值。
最终的分箱结果:
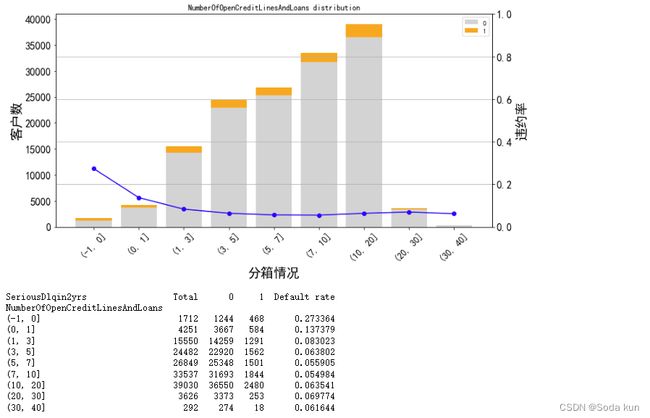
cut_num=[-1,0,1,3,5,7,10,20,30,40]
get_compare_plot(data,feature_plot="NumberOfOpenCreditLinesAndLoans",cut_num=cut_num,is_qcut=False)随着信贷数量增加,客户违约率在不断降低,最后基本保持在0.06左右。即信贷数量越多,说明该客户越值得信赖。
这里可以认定大于30的为异常值,因为30-40的样本量突然下降。
但也可以通过箱线图看出,30-40的值为连续的,没有断点。这里先不按照异常值进行处理。
抵押贷款和房地产贷款数量-NumberRealEstateLoansOrLines
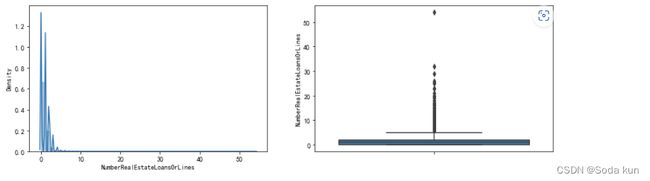
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(data['NumberRealEstateLoansOrLines'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=data['NumberRealEstateLoansOrLines'])
plt.show()通过直方图能看到数据是极度右偏的分布,另外箱线图上也能明显地看到离群点。
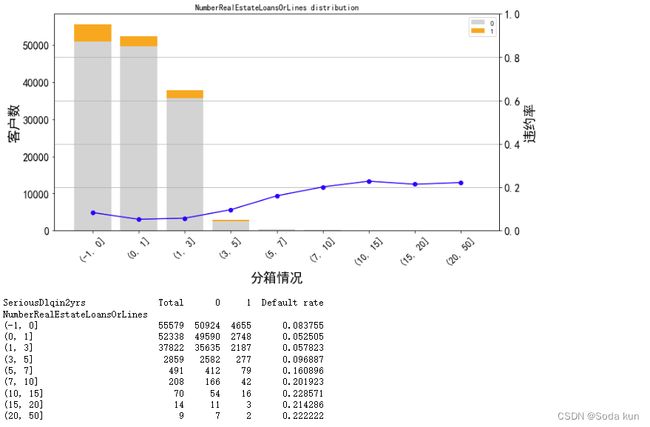
## 将大于20的分成一箱
cut_num=[-1,0,1,3,5,7,10,15,20,50]
get_compare_plot(data,feature_plot="NumberRealEstateLoansOrLines",cut_num=cut_num,is_qcut=False)当抵押贷款和房地产贷款数量为0时,客户有一定的违约率,跟之前的负债率一样。
当抵押贷款和房地产贷款数量大于0之后,随着数量的增加,客户违约率也在不断增加,说明整体的趋势应该是随数量增加而增大的。
但是大于10之后,随数量增加,客户数越小,所以决定将大于7的分成一箱,并且单调性和前面保持一样。
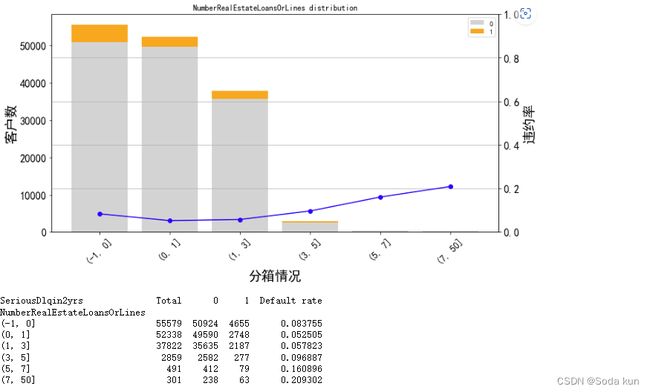
## 将大于7的分成一箱
cut_num=[-1,0,1,3,5,7,50]
get_compare_plot(data,feature_plot="NumberRealEstateLoansOrLines",cut_num=cut_num,is_qcut=False)家属人数(配偶,子女等)-NumberOfDependents
a=data['NumberOfDependents'].isnull().sum()/len(data)*100
print('家属人数缺失值比例为%.2f%%'%(a))家属人数缺失值比例为2.56%。家属人数存在缺失值,这里可看到缺失值的比例为2.62%。数值不大,可以使用众数填充。
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(data['NumberOfDependents'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=data['NumberOfDependents'])
plt.show()最终分箱结果:
## 将大于5的可分为一箱处理
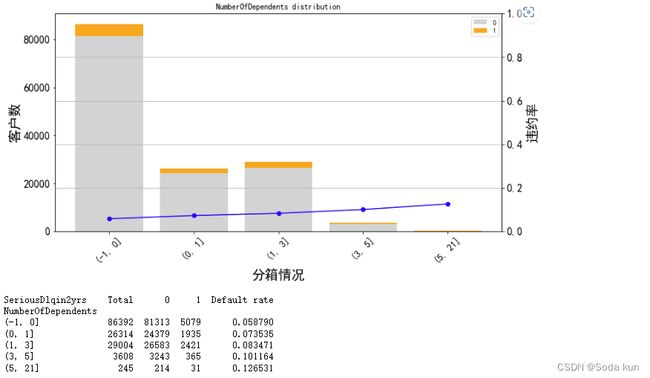
cut_num=[-1,0,1,3,5,21]
get_compare_plot(data,feature_plot="NumberOfDependents",cut_num=cut_num,is_qcut=False)随着家属人数增加,客户违约率增加。因为家属人数增加,家庭开销增加,需要的开销也就增加。当单身时(家属人数为0)客户违约率最小为0.058。 大于5的可以分成一箱。
总结:因为是比赛数据,所以结合业务情况在找数据中异常值的时候,没有做太多的异常值删除等操作,原因是在测试集当中也出现了同样的问题,为保证在测试集中良好的表现,所以只针对测试集中不存在的数据,比如年龄为0等这样的情况进行异常值删除。在实际业务情况下,我认为应该对这些问题积极和业务人员进行沟通。
2.4 数据预处理
这里对一些之前整理过的异常值处理,填补缺失值和数据不平衡处理的方法。
2.4.1 缺失值处理
##使用家属人数的均值对家属人数中的缺失值进行填补,inplace=true表示覆盖原数据
data["NumberOfDependents"].fillna(data["NumberOfDependents"].mean(),inplace = True)data.info() ##查看NumberOfDependent这一列填补上def fill_missing_rf(X,y,to_fill):
##使用随机森林填补一个特征的缺失值的函数
##参数:
##X:要填补的特征矩阵
##y:完整的,没有缺失值的标签
##to_fill:字符串,要填补的那一列的名称
#构建我们的新特征矩阵和新标签
df = X.copy()
fill = df.loc[:,to_fill]
df = pd.concat([df.loc[:,df.columns!=to_fill],pd.DataFrame(y)],axis = 1)
#找出我们的训练集和测试集
Ytrain = fill[fill.notnull()]
Ytest = fill[fill.isnull()]
Xtrain = df.iloc[Ytrain.index,:]
Xtest = df.iloc[Ytest.index,:]
#用随机森林回归来填补缺失值
from sklearn.ensemble import RandomForestRegressor as rfr
rfr = rfr(n_estimators=100).fit(Xtrain,Ytrain)
Ypredict = rfr.predict(Xtest)
return Ypredict##创建函数所需要的参数,并将参数导入到函数之中,产出结果:
X = data.iloc[:,1:] ##将特征赋予到x中
y = data["SeriousDlqin2yrs"] ##标签赋予到y中,也可以用 y =data.iloc[:,0]
X.shapey_pred = fill_missing_rf(X,y,"MonthlyIncome") ##将参数赋予到随机森林中##确认我们的结果合理之后,就可以将数据进行覆盖
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_preddata.info() ##检查全部都填满2.4.2 删除之前分析年龄为0的异常值
##观察异常值,年龄最小的值居然只有0,这不符合现实银行的业务需求,即使是儿童账户也要至少8岁,我们可以查看一下年龄为0的人有多少
(data["age"]==0).sum()只有1个人
##发现只有一个人年龄为0,可以判断这是录入失误造成的,可以当成是缺失值来处理,直接删除掉这个样本
data = data[data["age"]!=0]另外,有三个指标看起来很奇怪:"NumberOfTime3059DaysPastDueNotWorse"、"NumberOfTime60-89DaysPastDueNotWorse"、"NumberOfTimes90DaysLate"这三个指标分别是“过去两年内出现35-59天逾期但是没有发展的更坏的次数”,“过去两年内出现60-89天逾期但是没有发展的更坏的次数”,“过去两年内出现90天逾期的次数”。这三个指标,在99%的分布的时候依然是2,最大值却是
98,看起来非常奇怪。一个人在过去两年内逾期35~59天98次,一年6个60天,两年内逾期98次这是怎么算出来的?我们可以去咨询业务人员,请教他们这个逾期次数是如何计算的。如果这个指标是正常的,那这些两年内逾期了98次的客户,应该都是坏客户。在我们无法询问他们情况下,我们查看一下有多少个样本存在这种异常:
data.loc[:,"NumberOfTimes90DaysLate"].value_counts()data.loc[:,"NumberOfTime30-59DaysPastDueNotWorse"].value_counts()data.loc[:,"NumberOfTime60-89DaysPastDueNotWorse"].value_counts()data = data[data.loc[:,"NumberOfTimes90DaysLate"] < 90]data.index = range(data.shape[0]) ##恢复索引
data.info()2.5 特征衍生
构建两个新的特征:总违约率和每个月的支出
## 代表了客户在过去2年内逾期30-59天、60-89天和90天以上的总次数。
data['AllNumlate']=data['NumberOfTime30-59DaysPastDueNotWorse']+data['NumberOfTime60-89DaysPastDueNotWorse']+data['NumberOfTimes90DaysLate']
## 代表了客户每月债务还款额的大小。
data['Monthlypayment']=data['DebtRatio']*data['MonthlyIncome']2.5.1 解决样本不平衡问题
#探索标签的分布
X = data.iloc[:,1:]
y = data.iloc[:,0]y.value_counts()0 139292 1 9873
import imblearn
from imblearn.over_sampling import SMOTE
##imblearn是专门处理不平衡数据集的库,在处理样本不平衡问题中性能高过sklearn很多
#imblearn里面也是一个个的类,也需要进行实例化,fit拟合,和sklearn用法类似
X.copy().fillna(-1).reset_index(drop=True)
y = y.reset_index(drop=True)
sm = SMOTE(random_state=42) ##实例化
X,y = sm.fit_sample(X,y) ##返回已经上采样完毕过后的特征矩阵和标签
n_sample_ = X.shape[0]处理数据中正负样本比例不均衡,为了尽可能捕捉坏样本。这里采用SMOTE算法对数据进行上采样。
print(X.shape)
print(Y.shape)
pd.Series(y).value_counts()1 139292 0 139292 Name: SeriousDlqin2yrs, dtype: int64
本篇总结:
通过对数据进行探索性分析,更加了解数据,从中观察出数据的一些规律和问题,这样在后续的预处理过程中,也能有些思路。
以上是对数据分析和处理的过程,但其中还有很多的细节处理不到位,或者对业务理解上有偏差,如果大家有更好的见解可以多多指正,谢谢!
接下来是对数据进行分箱。使用toad这个专门的评分卡库自动分箱并构建逻辑回归模型来进行预测,并利用ROC-AUC和KS进行评估。再和使用手动分箱的方式进行对比,最后建立评分卡。
数据挖掘项目:金融银行风控信用评分卡模型(下篇)_Soda kun的博客-CSDN博客