数据结构: 第四章 串
文章目录
- 一、串的定义和实现
-
- 1.1串的定义和基本操作
-
- 1.1.1串的定义
- 1.1.2串的基本操作
- 1.1.3小结
- 1.2串的存储结构
-
- 1.2.1顺序存储
- 1.2.2链式存储
- 1.2.3基于顺序存储实现基本操作
- 1.2.4小结
- 二、串的模式匹配
-
- 2.1什么是字符串的模式匹配
- 2.2朴素模式匹配算法
- 2.3KMP算法
- 2.4求next数组
- 2.5KMP算法的进一步优化
一、串的定义和实现
所谓串其实就是字符串,该小节我们会先学习串的定义和相关基本操作。也就是要探讨它的逻辑结构和基本运算(数据结构三要素:逻辑结构、存储结构、数据的运算)
1.1串的定义和基本操作
1.1.1串的定义
串,即字符串(String)是由零个或多个字符组成的有序序列。
一般记为S=‘a1a2…an’(n>=0)
其中,S是串名,单引号括起来的字符序列是串的值,ai可以是字母、数字或者其他字符串,串中字符的个数n称为串的长度。n=0时的串称为空串。

ps:不同的编程语言对字符串的引号规定不同,java和c是双引号,python是单引号
子串:串中任意个连续的字符组成的子序列

主串:包含子串的串。
字符在主串中的位置:字符在串中的序号(需要注意的是,字符编号从1开始)

子串在主串中的位置:子串的第一个字符在主串中的位置

空串vs空格串:如下图,M的单引号里面啥也没有,是一个空串,长度为0。而N两个单引号之间是有几个空格字符的(我们这里是打了三个空格),所以N这个字符串,它的长度是3而不是0

字符串这种数据结构,它的逻辑特性看起来和我们之前学习的线性表非常相似,线性表也是由多个数据元素组成的有序序列,事实上,串也是一种特殊的线性表

串和线性表区别就是:普通的线性表,里面存放的数据元素可以是各种各样的数据类型,而串(字符串)这种数据结构,它的各个数据元素一定是字符

1.1.2串的基本操作
![]()
StrAssign(&T,chars):赋值操作,把串T赋值为chars
StrCopy(&T,S):复制操作,由串S复制得到串T
StrEmpty(S):判空操作,若S为空串返回True,否则返回False
StrLength(S):求串长,返回串S的元素个数
ClearString(&S):清空操作,将S清为空串
DestroyString:销毁串,将串S销毁(回收存储空间)
Concat(&T,S1,S2):串联接,用T返回由S1,S2联接组成的新串
![]()
SubString(&Sub,S,pos,len):求子串,用Sub返回串S的第pos个字符起长度为len的子串
![]()
Index(S,T):定位操作,若主串S中存在与串T值相同的子串,返回它在主串S中第一次出现的位置,否则函数值为0

StrCompare(S,T):比较操作。若S>T,则返回值>0;若S=T,则放值=0;若S
1.1.3小结
1.2串的存储结构
1.2.1顺序存储
//静态数组实现(定长顺序存储)
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN];//每个分量存储一个字符
int length;//串实际长度
}SString;
如果用这种方式,当你声明一个静态的字符串,系统会为你开辟如下空间来存放你的各个字符,每个字符(char类型)占1字节。当然了,也需要一小片空间来存放length变量。

而我们知道,这种静态数组的缺点就是数组长度不可变。我们现在预设的大小是255,如果后面遇到长度大于255的,存不下了,想拓展这个数组是不可能的。所以我们又称之为定长的顺序存储(本身还是一个静态数组,和线性表一样),该中方式,内存空间在使用结束系统会自动回收。
如果想实现可变大小,就可以用动态数组的方式来实现,也就是在你的结构体里面定义一个基地址的指针,然后用malloc申请一整片连续的存储空间,让基地址指针指向这片空间的起始地址。
//动态数组实现(堆分配存储)
typedef struct{
char *ch;//按串长分配存储区,ch指向串的基地址
int length;//串的长度
}HString;
HString S;
S.ch=(char*)malloc(MAXLEN*sizeof(char));
S.length=0;
需要注意的是,malloc函数申请的内存空间属于堆区,所以这周实现方式又称为堆分配存储(本身还是一个动态数组)
堆区的内存空间,你需要手动的free掉之前malloc的空间
下面是串顺序存储的4个实现方案

ps:对于方案二,虽然是节省了末尾的一个空间,但是由于char[0]作为存储长度的空间,char类型只有1字节,也就是8比特位,所以只能存储0-255的数,如果字符串长超过就会有问题了。
教材中的方案4,是方案1和方案2的结合,我们舍弃char[0]的位置,这样第i个数正好对应i下标。而且用int类型的length存储字符串长度范围会比char类型存储长度更大。
1.2.2链式存储
链式存储和线性表也一样的,如下
typedef struct StringNode{
char ch;//每个结点存1个字符
struct StringNode *next;
}StringNode,*String;
我们用每一个如上的结点来存一个字符和一个指针来指向下一结点。需要注意的是,我们这里一个char是一个字符,char大小只有1字节,但是一个指针大小4字节。这就意味着,你用1字节空间存储实际想要的信息,却还要花4字节空间存储一个辅助信息,这种情况就称为存储密度低
ps:存储密度低也就是实际有用的信息所占的比例非常小
如何解决存储密度低的问题呢?我们可以让每一个结点存储多个字符,如下:
typedef struct StringNode{
char ch[4];//每个结点存多个字符
struct StringNode* next;
}StringNode,*String;

这里是结点中定义的是ch[4],也就是每个结点存4字符,你也可以改成别的数字,让一个结点存的更多。
这样的话,每个结点中实际有用的信息所占的空间比例就高了,即存储密度提高了。所以,如果要用链式存储实现串,一般来说推荐该中方式。
1.2.3基于顺序存储实现基本操作
SubString(&Sub,S,pos,len):求子串,用Sub返回串S的第pos个字符开始,长度为len的子串
举个例子,如下图我们存储了wangdao这七个字符串,我们传pos=4,len=3过去,也就是要4号下标,长度为3的子串gda,如下图:

#define MAXLEN 255
typedef struct{
char ch[MAXLEN];
int length;
}SString;
//求子串
bool SubString(SString &Sub,SString S,int pos,int len){
//子串范围越界
if(pos+len-1>S.length)
return false;
for(int i=pos;i<pos+len;i++)
{
Sub.ch[i-pos+1]=S.ch[i];
}
Sub.length=len;
return true;
}
StrCompare(S,T):比较操作,若S>T,则返回值>0;若S=T,则返回值=0;若S
如何比较两个字符串大小?比如有两个字符串S和T,从它们第一个字符开始比较,如果相同则比较它们下一个字符,如果不相同,则哪个字符大哪个字符串就大——先出现更大字符的那个字符串更大,还有一种情况就是两个字符串扫描过的字符都相同则长度长的串更大,比如abc和abcd,abcd更大
//比较操作,若S>T,则返回值>0;若S=T,则返回值=0;若S
int StrCompare(SString S,SString T){
for(int i=1;i<S.length&&i<=T.length;i++)
{
if(S.ch[i]!=T.ch[i])
return S.ch[i]-T.ch[i];
}
//扫描过的所有字符都相同,则长度大的串更大
return S.length-T.length;
}
Index(S,T):定位操作,若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置,否则函数值为0
怎么确定位置呢?举个例子,我们现在有S和T两个字符串,要在主串S中找出串T相同的子串:
假设S和T如下,T长度为3:
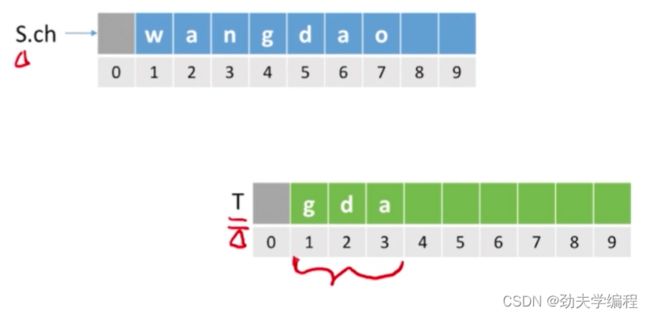
我们可以用刚才实现的两个基本操作,用第一个取子串的操作,我们从主串S中取下长度为3的子串,如下

再用刚才讲的比较操作,看从S中取下的子串是否与T相等
如果不等,我们就在S中往后一位,继续取长度为3的子串与T对比

然后以此类推,直到在S中找到一个子串和T相等,然后返回子串第一个字符的位序即可。

int Index(SString S,SString T){
int i=1,n=StrLength(S),m=StrLength(T);
SString sub;//用于暂存子串
while(i<=n-m+1){
SubString(sub,S,i,m);
if(StrCompare(sub,T)!=0){
i++;
}
else{
return i;//返回子串在主串中的位置
}
}
return 0;//S中不存在与T相等的子串
}
1.2.4小结
二、串的模式匹配
2.1什么是字符串的模式匹配
模式匹配算法听起来好像很nb,其实并没有什么。我们来看两个例子就知道啥是模式匹配了。
你用word文档的时候,是不是经常使用一个搜索功能:就是你输入一段文字,然后word给你搜这段文字。
还有就是你用搜索引擎的时候,是不是也经常会输入一段文字,然后搜索引擎给你在网页里面匹配和这个文章相同的子串。
这就是字符串的匹配模式,其实就是要在字符串里面搜索某一段内容
从一整段字符串中搜索内容,被搜索的字符串我们称为主串。
而我们想搜索的内容,称为模式串,需要注意,模式串不一定能在主串中找到。
子串:是主串的一部分,是一定可以在主串中找到的。
所谓字符串的模式匹配,就是指我们在主串中找到与模式串相同的子串,并返回子串的位置。

2.2朴素模式匹配算法
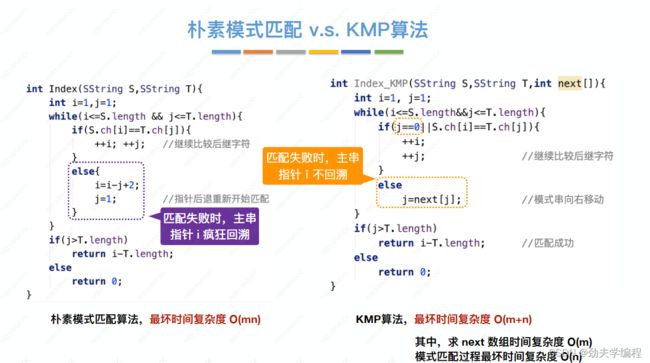
既然它都说是朴素了嘛,朴素的宗旨就是最简单,就是暴力解决。
比如我们下面两个字符串:主串S和模式串T
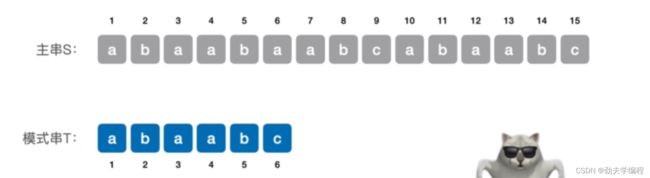
模式串T长度是6,我们就把主串中所有长度为6的子串与它进行比较呗。
我们从主串中找出第一个长度为6的子串,该子串和模式串进行对比,如果不匹配,就再对比下一个。如果下一个子串还不匹配,就再下一个,以此类推。。。。
我们把所有的这些子串都和模式串进行一个对比,这样肯定是没有遗漏的进行一个匹配了。但是也有可能当我们对比完最后一个子串发现没有子串和模式串匹配,这种情况就是匹配失败。

长度为n的主串,长度为m的子串有n-m+1个
学的比较扎实的同学会发现,我们之前学习串的Index函数不就是朴素模式匹配的思想吗?如下图:

接下来我们将介绍,如何直接通过操作数组下标来实现朴素模式匹配算法:
现有主串S和模式串T:

我们设置两个扫描指针i和j,这两个指针指到哪,我们就把字符对比到哪
如上动态图所示,刚开始要对比的就是主串的第一个字符和模式串的第一个字符,如果这两个字符相等,就让i和j往后移。然后重复进行比较和后移操作,直到我们发现最后一个位置i和j指向的字符不等。
不等就说明匹配失败了,第一个子串和这个模式串是没有匹配上的,那么我们就该匹配第二个子串位置了,而第二个子串的起始位置应该是在2号位
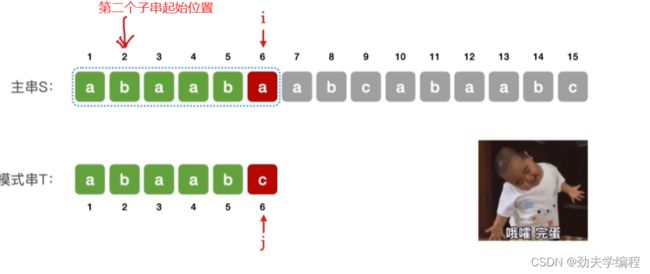
所以,在我们处理时,如果发现当前的子串匹配失败,那么我们主串的扫描指针i应该让它指向下一个子串的第一个位置,而模式串的指针j应该回到模式串的第一个位置。
写成代码就是i=i-j+2; j=1;
j当前的值说明了我们现在匹配到了子串的第几个字符,我们让i-j就得到了目前子串的前一个位置,再+2就是下一个子串的第一个位置。
因此,当前子串匹配失败后i=i-j+2,i会变成2,而j会变成1。
然后就是开始匹配第二个子串和模式串T,发现第2个字符就不一样

匹配第三个子串,发现第2个字符不一样

匹配第四个子串,发现六个字符都可以匹配成功,因为每次匹配成功i++; j++,所以此时j会超出模式串的长度

所以,若j>T.Length,则当前子串匹配成功,返回当前子串第一个字符的位置,也就是i-T.Length
我们这里给出朴素模式算法的代码实现:
int Index(SString S,SString T){
int i=1;j=1;
while(i<=S.length&&j<=T.length){
if(S.ch[i]==T.ch[i]){
i++;//继续比较后续字符
j++;
}
else{
i=i-j+2;//指针后退后重新开始匹配
j=1;
}
}
if(j>T.Length)
return i-T.Length;
else
return 0;
}
下面来分析一下该算法的最坏时间复杂度:假设主串长度为n,模式串长度m
如下例:主串S和模式串T都是除了最后一个是b其他全是a,

按照朴素模式匹配算法的规则,我们得先匹配主串第一个子串和模式串,一个字符一个字符依次往后对比。你会发现前面的字符都可以匹配,但是比到最后一个字符就匹配失败了。

接下来比较第二个字符串,让i到2的位置,j到1的位置。然后依次比较,又是到最后一个字符才发现比较失败。


后面以此类推,每个子串都要比较m个字符,一共n-m+1子串,时间复杂度O((n-m+1)*m)=O(nm)

2.3KMP算法
上小节我们学习了朴素模式匹配算法,KMP算法其实就是基于朴素模式匹配算法的优化。

举个例子:
现假设我们第一个子串在第六个字符匹配失败,那我们按照朴素模式匹配算法是不是就该匹配第二个子串了?
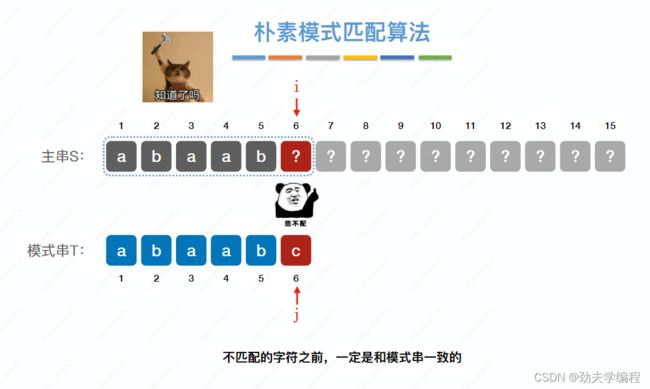
但是朴素模式匹配忽略了一个重要的信息:如果是第6个字符匹配失败,那么前5个字符一定是匹配成功的。
那么进入第二个子串的匹配:我们由第一个子串知道,第二个子串第1个字符是b,那么与模式串T第一个字符不匹配。那么第二个字符的第5个字符(图中6号位置)和第6个字符(图中7号位置)在本轮匹配中也就不用检查了

进入第三个子串的匹配:我们知道第三个子串第二个字符与模式串不匹配,后面也不用检查了。

进入第四个子串的匹配:我们发现第四个子串前两个已知的字符都是可以匹配的,那么就需要进行检查第四个子串的第3-6个字符了(图中6号下标到9号下标)

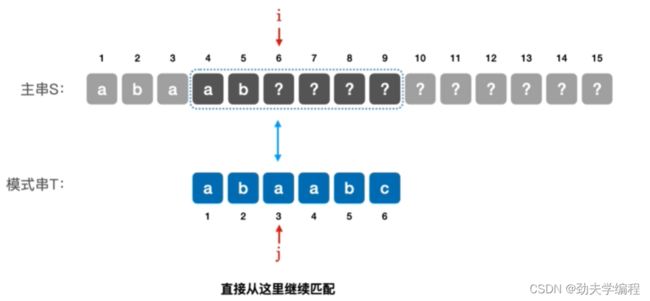
---------------------------我是分隔符------------------------------------
再来捋一遍:当我们匹配到某一个字符,该字符发生了失配。该字符前面的字符信息我们是可以确定的,它和模式串一定是保持一致的。
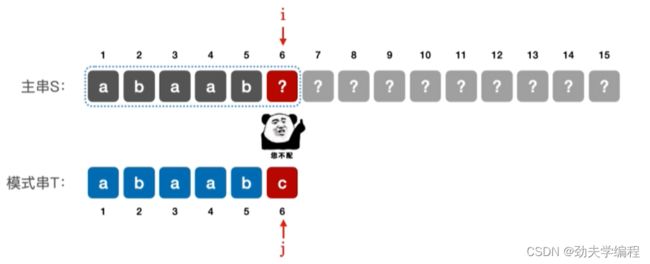
比如我们模式串abaabc,那么第一个子串第6个字符失配,我们就可以确定前5个字符为abaab,那么以第二个元素开头的子串和以第三个元素开头的子串就不用匹配了,直接匹配第四个元素开头的子串。
现确定主串S前5个元素为abaab
如果是第二个元素开头的子串,第一个字母是b,与模式串第一个字符a不匹配
如果是第三个元素开头的子串,前两个字母是aa,与模式串前两个字符ab不匹配
而对于第四个子串来说,我们也没必要对比第四个子串的前两个字符,因为我们可以确定这两个元素肯定是和模式串能匹配的

现在暂时还不能确定的是我们模式串的第三元素和主串里面刚才失配的元素是否匹配
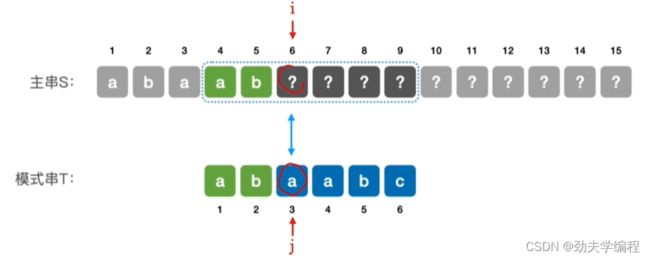
因此对于模式串T='abaabc’来说,当第6个元素匹配失败时,可令主串指针i不变,模式串指针j=3,也就是从模式串的第三个元素开始匹配。
因此可以看到,我们利用好模式串本身的信息,可以跳过很多没必要的对比。对于当前的模式串和主串来说,我们是跳过了中间的几个子串,也跳过了第四个子串前两个字符,直接从第四个子串第三字符开始比较,如下图:
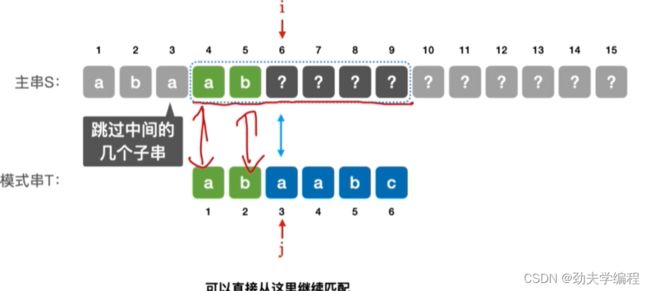
这就是KMP算法的思想,要利用好模式串本身隐含的一些信息,然后要确定模式串某个元素发生失配时,我们要如何处理。
显然,这里得到的结论并不依赖于主串,只和模式串有关。和我们匹配的是主串的哪个位置并没有关系
再来具体应用一下,如果我们现在从主串的第五个位置开始尝试匹配。同样的,我们匹配到该子串最后一个元素时发生失配,我们可以知道前面几个字符肯定是一样的

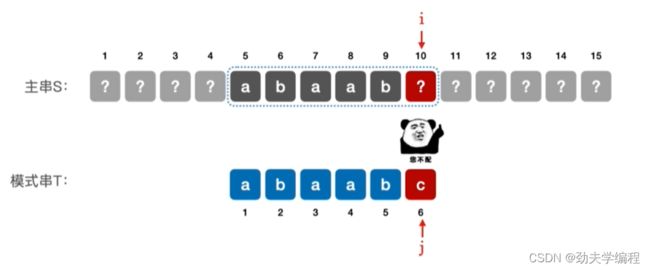
那么根据刚才的结论,第六个字符失配时,主串指针i不变,模式串指针j变成3
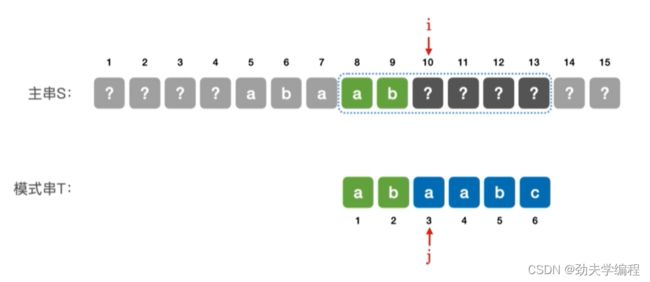
也就是直接跳过了中间几个子串的对比,然后当前这个子串也是从第三个元素开始往后匹配。
因为刚才发生失配的元素到底是什么我们不知道,因此,它有可能和我们模式串第三个元素能匹配上。
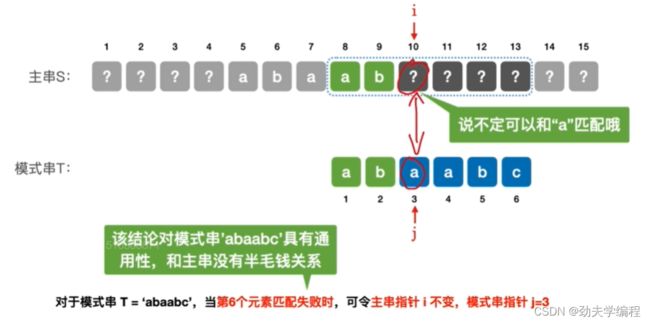
到这里,我们探讨的是这个模式串的第六个元素发生失配的情况我们该怎么办,接下来顺着这个思路我们把其他情况考虑一下。
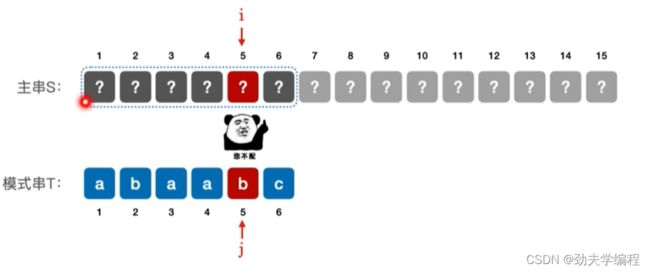
对于模式串T=‘abaabc’,当第5个元素匹配失败,怎么办?
第五个元素发生失配,那么前面4个元素信息我们是知道的
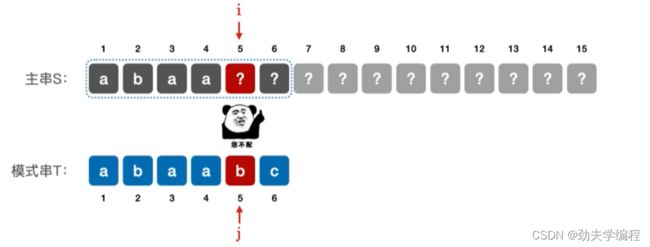
那么第二个子串能否匹配呢?显然也是不可以的,第二个子串第一个元素就失败了
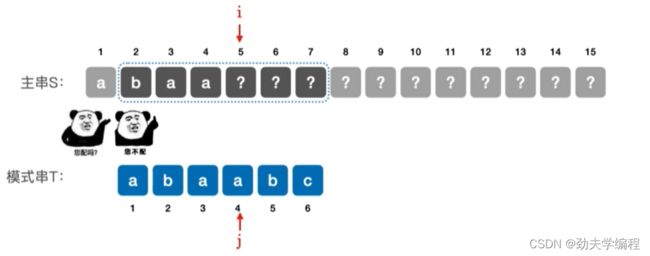
再看第三个子串,第三个子串第二个元素匹配失败

再看第四个子串,发现前面已知的信息是可以匹配上的。
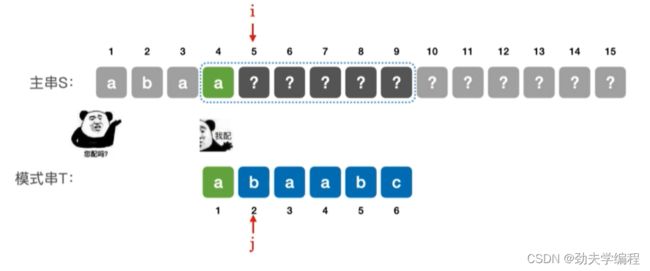
而刚才发生失配的字符我们不知道是什么,所以我们接下来从图中5号位置开始往后比较即可。
因此对于模式串T='abaabc’来说,当第5个元素匹配失败时,可令主串指针i不变,模式串指针j=2,也就是从模式串的第二个元素开始匹配。
对于模式串T=‘abaabc’,当第4个元素匹配失败,怎么办?
第四个元素匹配失败,前面3个元素的信息我们是可以知道的
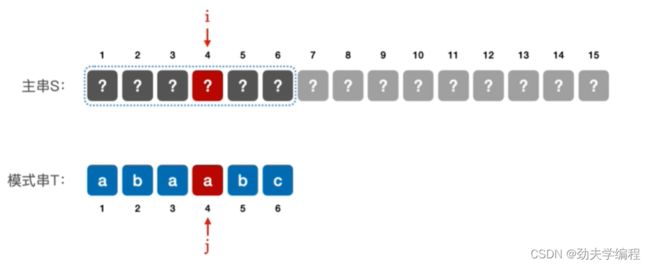
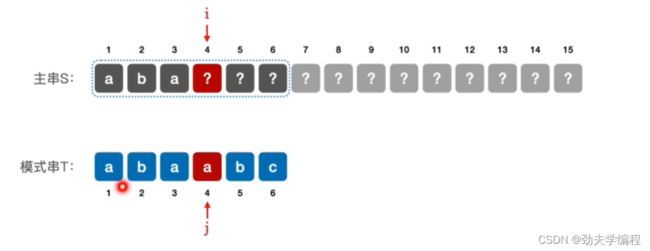
看第二个子串,发现第一个元素就无法匹配
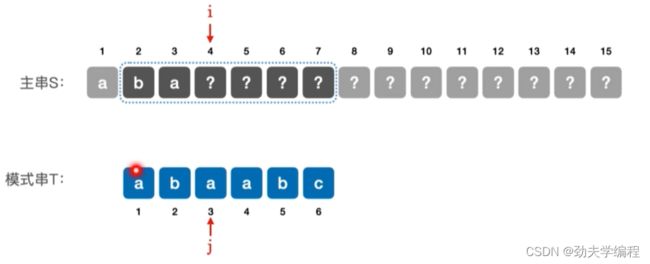
看第三个子串,发现已知的信息是可以和模式串匹配的。

接下来我们就从模式串j=2的位置往后匹配即可
因此对于模式串T='abaabc’来说,当第4个元素匹配失败时,可令主串指针i不变,模式串指针j=2,也就是从模式串的第二个元素开始匹配。
对于模式串T=‘abaabc’,当第3个元素匹配失败,怎么办?
第三个元素失配,那么前两个元素信息是已知的

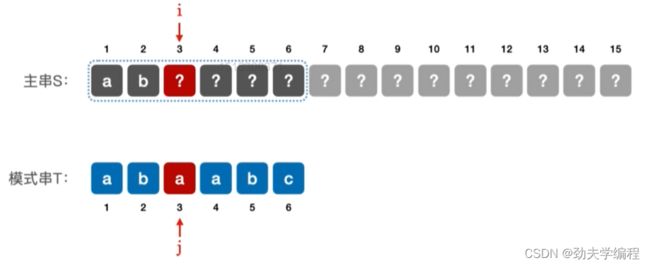
看第二个子串能否匹配,发现第一个元素就无法匹配

看第三个子串能否匹配,发现没有已知信息了。所以要从第三个子串第一个元素往后匹配

因此对于模式串T='abaabc’来说,当第3个元素匹配失败时,可令主串指针i不变,模式串指针j=1,也就是从模式串的第一个元素开始匹配。
对于模式串T=‘abaabc’,当第2个元素匹配失败,怎么办?

所以我们只能把下一个子串和模式串进行对比

因此对于模式串T='abaabc’来说,当第2个元素匹配失败时,可令主串指针i不变,模式串指针j=1,也就是从模式串的第一个元素开始匹配。
对于模式串T=‘abaabc’,当第1个元素匹配失败,怎么办?
那就直接下一个子串进行匹配呗!

和之前的几种情况不同的是,刚才的某个元素发生失配我们的主串指针i是不变的,j改变。
代码中怎么操作?我们先让j=0,也就是指向模式串第一个元素前一个位置,然后i和j统一++


然后对比后面的子串即可。
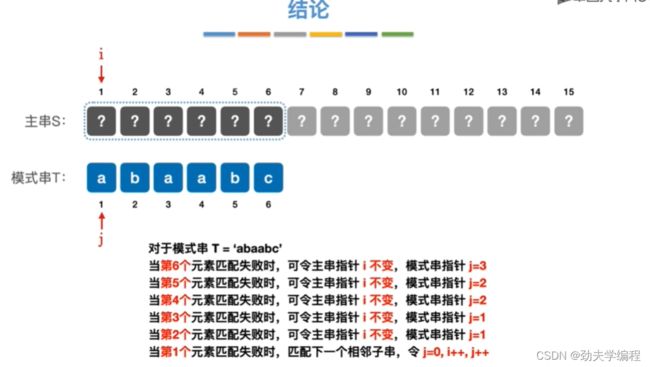
到这里,我们对于模式串T=‘abaabc’来说,它的每一个元素发生失配的情况我们就全考虑进去了
这种方式,我们主串的指针i一直往下走一遍就行了,不需要朴素模式中那种还要回头匹配,比朴素模式匹配效率高了非常多。
在模式匹配中,通常模式串是很短的,而主串可能非常的长,那么用我们这种策略,先分析模式串中的隐藏信息,再去进行匹配,非常高效!
而对于刚才的指针j的变化操作,我们可以用一个next数组来存储相关信息:
比如当第六个元素发生失配时,我们让j=3,对应数组信息就是next[6]=3
再比如当第五个元素发生失配时,我们让j=2,对应数组信息就是next[5]=2
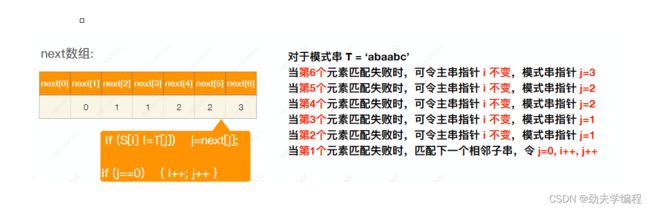
next数组就是指明了我们在某一个位置发生失配时,应该把j的值修改为多少。而比较特殊的是第一个元素就发生失配时,需要先把j修改为0,然后i和j统一++
我们的next数组是和模式串的值相关的,与主串无关。
所以,KMP算法的整体流程为:在进行模式匹配前,先进行一个预处理,要分析模式串,然后求出和模式串对应的next数组,然后再利用next数组进行模式匹配,整个匹配流程中,主串的指针i不需要回溯。

下一小节我们介绍如何求next数组,这里先学习如何利用next数组进行匹配
int Index_KMP(SString S,SString T,int next[]){
int i=1;j=1;
while(i<=S.length&&j<T.length){
if(j==0||S.ch[i]==T.ch[j]){
i++;
j++;//继续比较后续字符
}
else
j=next[j];//模式串向右移动
}
if(j>T.length)
return i-T.length;//匹配成功
else
return 0;
}
2.4求next数组
根据上小节的学习,我们知道了kmp算法的原理,首先我们需要根据模式串的值,求出与这个模式串相应的next数组,接下来基于这个next数组,来对模式串进行匹配。整个匹配的过程,主串的指针不回溯。

本节将介绍几个求next数组的例子,来帮大家达到手算next数组的水准。
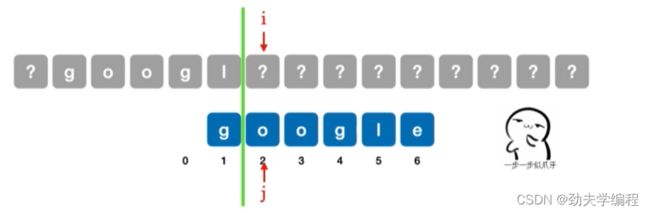
比如现在有google这一个字符串,其长度为6,我们创建一个next数组,next[j]表示模式串中第j个字符发生匹配失败时,指针j应该指向什么位置。

如果现在第1个字符匹配失败:
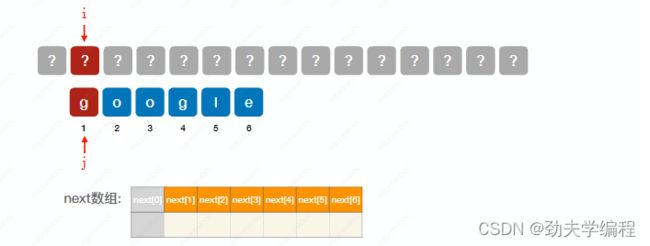
按照上小节分析的逻辑,应该是让j指针先等于0,然后i++,j++
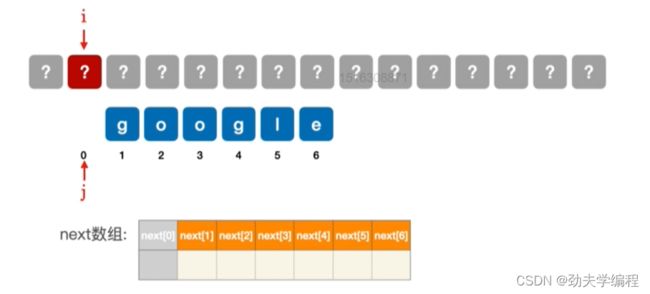
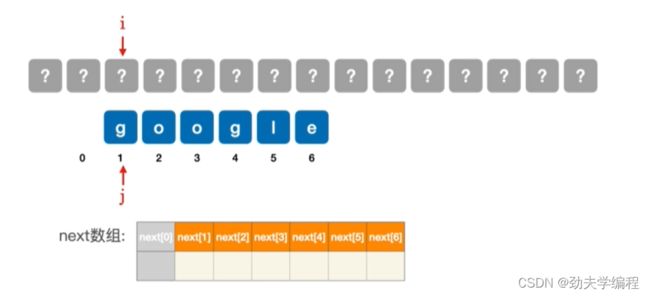
任何模式串都一样,第一个字符不匹配时,只能匹配下一个子串,因此next[1]无脑写0即可

如果现在第2个字符匹配失败:

如果是第二个字符匹配失败,那只能让模式串向右移动一位,也就是让j指向1这个位置。也就是让模式串i指向的字符和模式串第一个字符进行匹配。

任何模式串都一样,第二个字符不匹配时,应尝试匹配模式串第一个字符,因此next[2]无脑写1即可
如果现在第3个字符匹配失败:
第三个位置匹配失败,我们知道前两个位置是能匹配的。我们在不能匹配位置的前面画一条分界线,如下图

我们让模式串一步一步往右移动,在移动的过程中,观察分界线左边是否与主串匹配。
这里先往右移动一步,发现g和o是不匹配的,说明我们模式串移到这个位置是不够的。
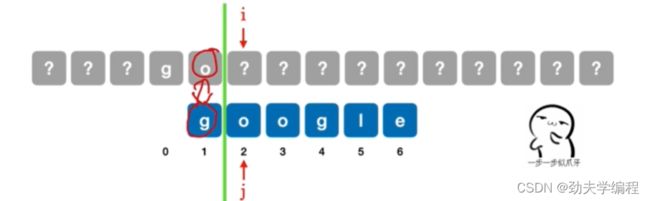
继续往右移动一位,到这里,整个模式串都移动到分界线右边了。
而此时分界线右边主串内容是什么,我们还不知道,所以让主串i指向的位置和模式串j指向的位置进行比较。
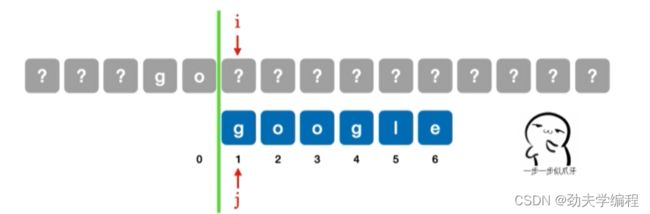
所以,当第三个字符匹配失败时,我们让j等于1

如果现在第4个字符匹配失败:
第4个字符匹配失败,说明前3个是可以匹配上的,我们在不能匹配字符前画一个分界线。
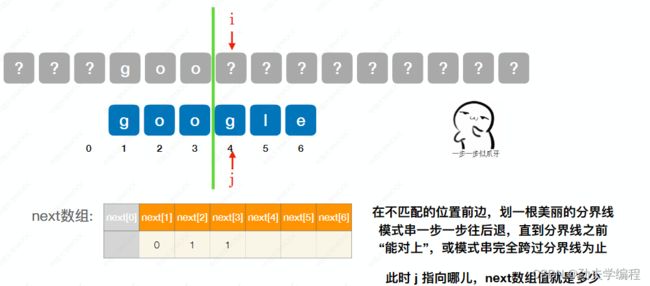
和刚才一样的方法,让模式串依次右移
移动一次,分界线左边和主串无法匹配

再次移动,分界线左边和主串无法匹配
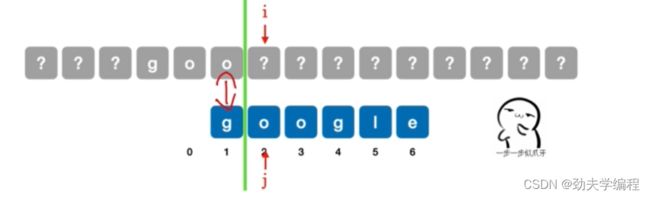
继续移动,发现模式串已经全部到分界线右边了,我们让主串i指向的位置和模式串第一个位置进行比较,也就是j=1
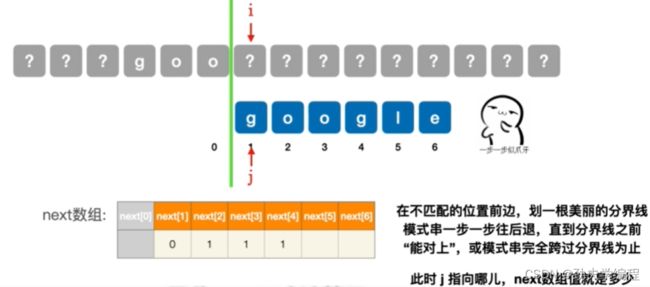
如果现在第5个字符匹配失败:
第五个元素匹配失败,说明前4个可以匹配,我们在不能匹配的字符前画一个分界线。然后让模式串依次右移

移动一次,分界线左边和主串无法匹配

再次移动,分界线左边依然无法匹配
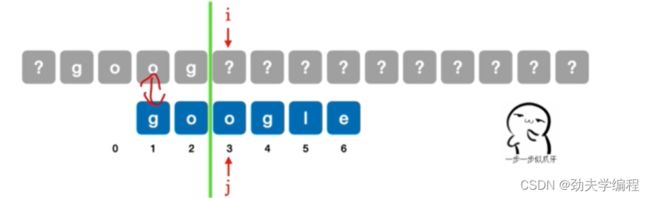
继续移动,分界线左边模式串和主串可以匹配了,我们接下来就是检查主串i指向的位置和模式串j指向的位置能否匹配,所以next[5]=2
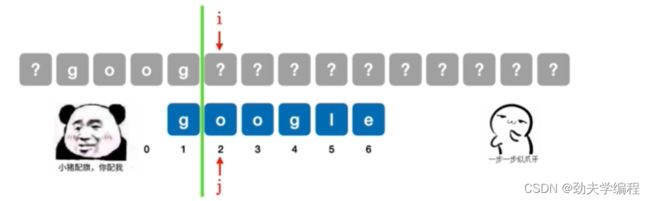

如果现在第6个字符匹配失败:
同理,在当前匹配失败的字符前画一个分界线。然后模式串依次右移。
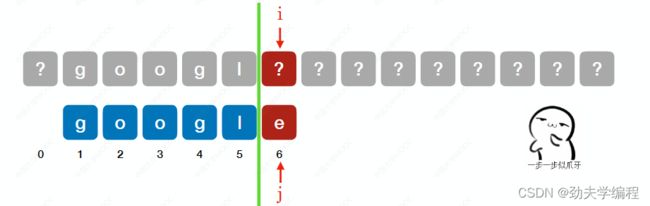
移动一次,分界线左边和主串无法匹配

移动两次,分界线左边和主串无法匹配

移动三次,分界线左边和主串无法匹配
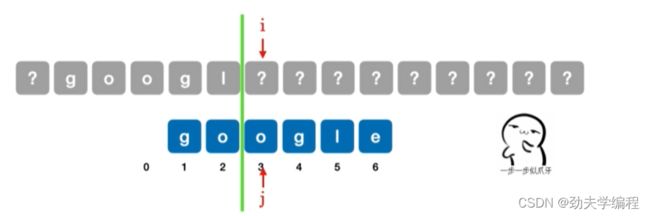
移动四次,分界线左边和主串无法匹配
继续移动,发现此时模式串已经全部到分界线右边了,那么就让主串i指向的字符和模式串第一个字符比较即可。
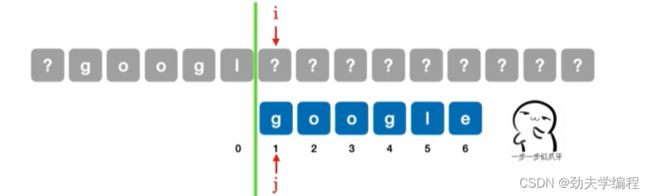

2.5KMP算法的进一步优化
上一小节我们介绍了如何手算求next数组,本小节将会介绍如何求nextval数组,也就是如何优化next数组。
现模式串T我们已求得next数组,如下图

现假设主串和模式串匹配到第3个字符时不匹配

如果是next数组,我们应该是看next[3]=1,也就是把j移动到模式串1号位置。
但是这里需要注意,我们模式串失配的3号位和1号位是同一个字符a。而模式串3号位的a和主串3号位不匹配,说明主串3号位一定不是a,那主串3号位肯定也没法和模式串一号位的a匹配啊。
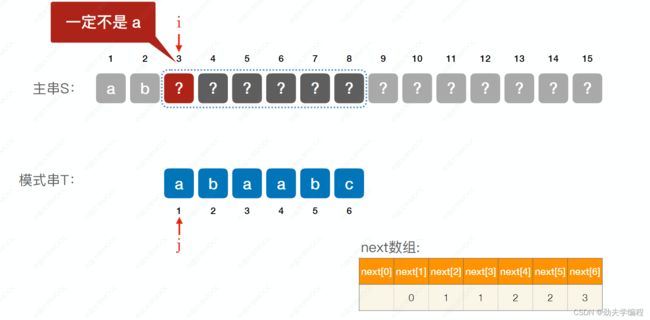
因为,1号位是一定会匹配失败的,所以,我们这里应该是让next[3]=0

然后由于主串4号位的内容我们还位置,接下来让i++,j++,即让i指向主串4号位,j指向模式串1号位,再让两者进行比较。
再来看一种情况,现假设主串和模式串匹配到第5个字符时不匹配
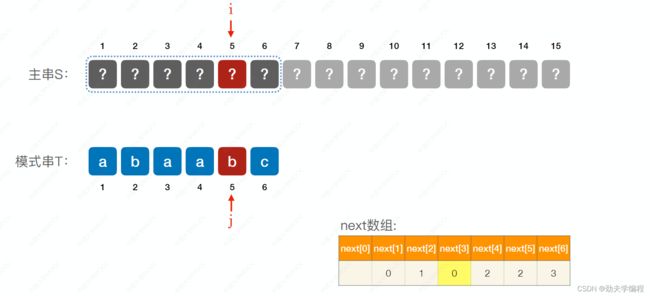
我们的next[5]=2,按道理应该是让j指向模式串的第2位。

但是和上一种情况类似的,我们模式串的5号位和2号位是相同的字符b,你模式串5号位不匹配了,模式串2号位能匹配?显然不能啊。
所以,这里我们应该是把next[5]=1,也就是让模式串1号位去和主串5号位进行匹配
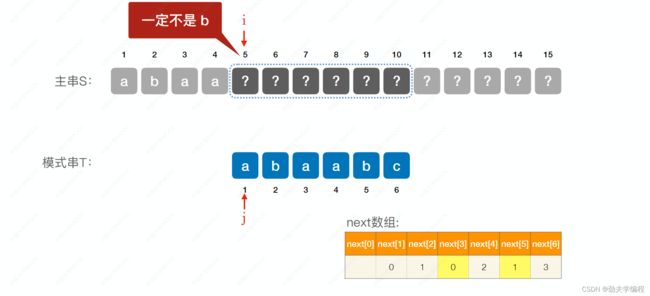
到这里,我们就完成了对next[3]和next[5]的优化,是不是所有的next[i]都可以被优化呢?也不是,来看一个例子
现假设主串和模式串匹配到第6个字符时不匹配
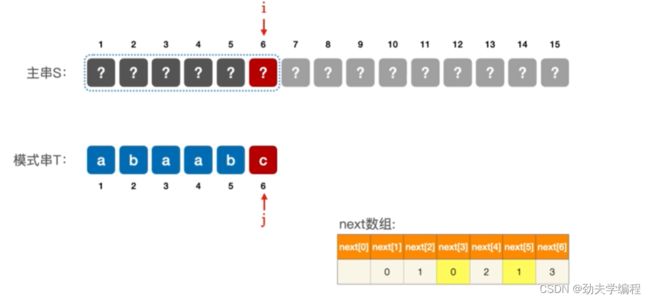
按照next[6]=3,应该是让j指向模式串3号位。
我们这里是模式串6号位的c与主串6号位不匹配,只能说明主串6号位不是c
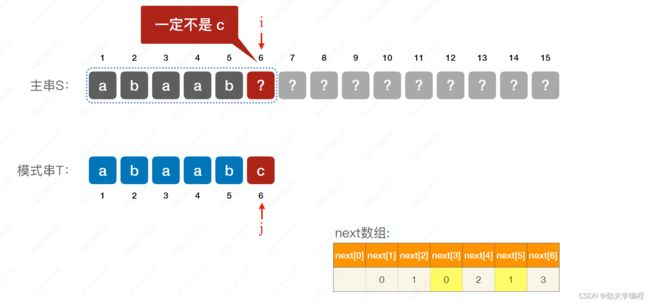
而next[6]=3是让j指向了模式串3号位的a。我们知道c与主串6号位不匹配,但不知道a与主串6号位是否匹配啊,所有这里next[6]=3是不能改的。
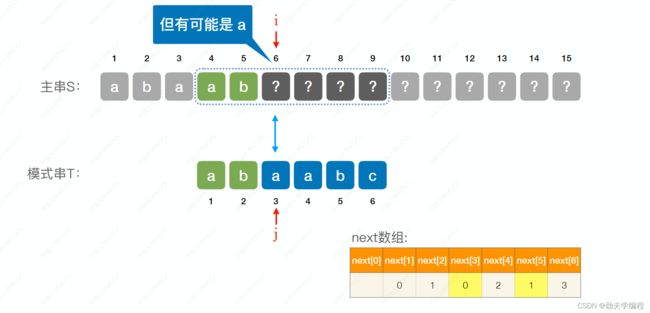
所有,我们总结一下next数组的优化思路:我们要判断next数组指向的字符和原本失配的字符,是否相同。如果相同就要优化,如果不同就无需操作。
事实上,我们只是优化了next数组,对kmp算法的整个逻辑是没改变的。
优化之前的kmp算法:首先根据模式串求next数组,然后利用next数组实现kmp算法。
优化之后的kmp算法:根据模式串求nextval数组(优化后的next数组),然后利用nextval数组实现kmp算法。
即把下图中next数组换成nextval数组即可。
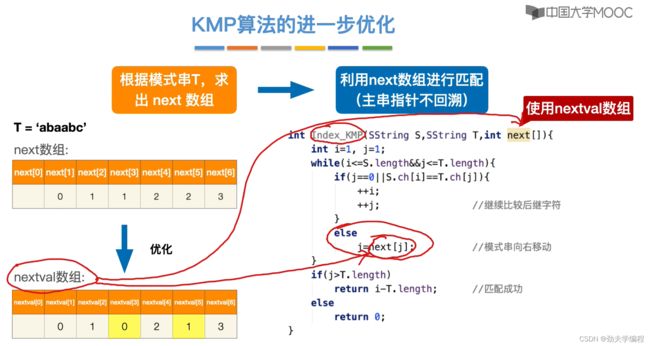
next数组中无脑写next[1]=0,next[2]=1
nextval数组中无脑写nextval[1]=0
如果当前next[j]所值的字符和当前j所指字符不相等,则nextval[j]=next[j]
如果当前next[j]所值的字符和当前j所指字符相等,nextval[j]=nextval[next[j]]
nextval[1]=0;
for (int j=2;j<T.length;j++){
if(T.ch[next[j]]==T.ch[j])
{
nextval[j]=nextval[next[j]];
}
else
{
nextval[j]=next[j];
}
}
练习题:
ps:
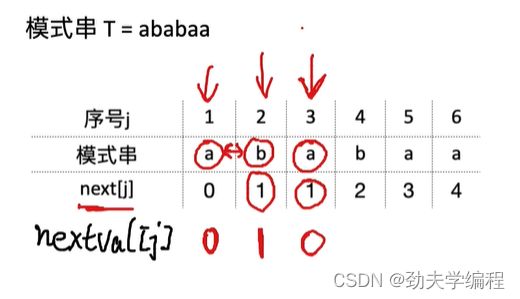
现有模式串ababaa,已求得其next数组如下图,要求你将next数组优化成nextval数组

首先,nextval[1]无脑写0

接下来,我们依次往后求nextval[j]的值
现在j=2,所指元素为b。next[2]=1,所指元素为a。
两个元素不相等,直接让nextval[2]=next[2]

j=3,所指元素为a。next[3]=1,所指元素为a。
两个元素相等,让nextval[3]=nextval[next[3]],也就是nextval[3]=nextval[1]
因为j=3和j=1所指字符相同,j=3匹配失败,j跳到next[3]所指位置,即j=next[3]=1
但是j=1也注定匹配失败,所以这里再让j跳到nextval[1]的位置。
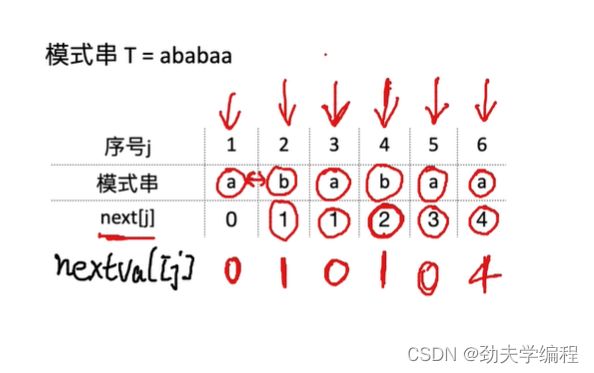
j=4,所指元素为b,next[4]所指元素也是b。
两个元素相等,让让nextval[4]=nextval[next[4]]
即nextval[4]=nextval[2]=1

j=5,所指元素为a,next[5]所指元素也是a。
两个元素相等,让让nextval[5]=nextval[next[5]]
即nextval[5]=nextval[3]=0

j=6,所指元素为a。next[6]=4,所指元素为b。
两个元素不相等,直接让nextval[6]=next[6]
考试中kmp算法多以选择题出现,大家会手算next数组和nextval数组即可