A* 算法详解(超级详细讲解,附有大图)
目录
引入
一.基本概念
二.算法原理
①用宽度优先搜索
②狄克斯特拉算法
③A*算法
三.需要注意
四.c++伪代码
最后
引入
今天想跟大家聊的,是我们经常用到,但是却让大家觉得十分神秘的那个算法:A* 。
这是一个远古而又非常经典的游戏——红警和贪玩蓝月
玩的时候,就会发现这里面的兵,你只要指定好地点,他们就会自己朝目的地进发,最终去向你指定的地点。。。(这段是看了别人的文章之后乱编出来的)
很多游戏也是这样,它会将你指定的人物,以一定的路径,到达某地(逐渐抽象)。简单来说,就是寻路。
在游戏,乃至生活之中,在很多地方会有寻路的需求。而我们因为各种原因,总会寻求最短的路线,在计算机科学中,这种寻求最短路径的问题统称为最短路径问题。
而A*(star)算法,则是求最短路问题中的一种较好算法。
一.基本概念
本期,我将通过广度优先搜索、狄克斯特拉算法来讲A*算法。
广度优先搜索:从起点开始,有由近及远进行广泛搜索。不仅适用于常规路径查找,还适用于程序地图生成、流场寻路、距离映射和其他类型的地图分析。不过,时间复杂度较大,当终点离起点较远时,搜索时间会比较长。
狄克斯特拉算法:狄克斯特拉算法让我们考虑需要探索路径的优先级。它不是平等地探索所有可能的路径,而是倾向于探索移动成本较低的路径。不足之处在于将其他的顶点的最短路径也计算出来,而这部分是无用的。
A*算法 :在狄克斯特拉算法的基础上,选取路径时,会先估算一个值,以此省去一些无用的计算。
二.算法原理
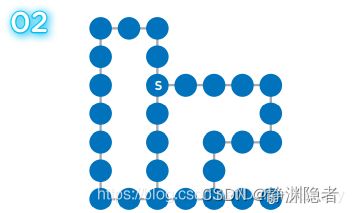
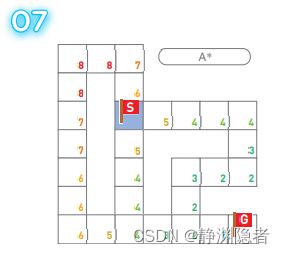
现在,给出一个迷宫,请你求出起点S到终点G的最短路线。
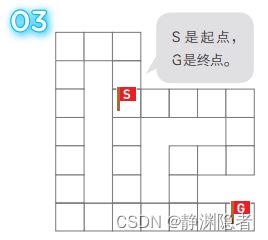
我们可以把迷宫看作是一个图,其中每个方块都是一个顶点,各顶点间的距离都为1.就像这样:
那么,我们就可以做了。
①用宽度优先搜索
用宽度优先搜索求最短路径的结果会如上图所示,方块中的数字表示从起点到该顶点的距离,蓝色和红色的方块表示搜索过的区域,红色方块同时还表示从S到G的最短路径。很显然,宽度优先搜索是一种盲目的查找,比较暴力。
②狄克斯特拉算法
用狄克斯特拉算法求最短路径的结果会如上图所示,方块中的数字表示从起点到该顶点的距离(权重),蓝色和橙色的方块表示搜索过的区域,橙色方块同时还表示从S到G的最短路径。
狄克斯特拉算法只根据起点到候补顶点的距离来决定下一个顶点。因此,它无法发现蓝色箭头所指的这两条路径其实离终点越来越远,同样会继续搜索。
这时候,我们就需要A*算法了。
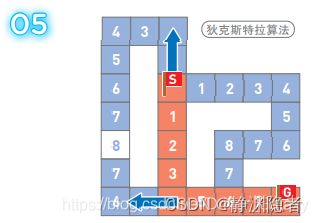
③A*算法
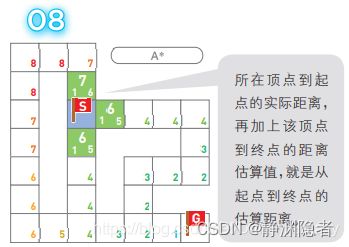
而A*算法不仅会考虑从起点到候补顶点的距离, 还会考虑从当前所在顶点到终点的估算距离。此处我们用的是 将顶点到终点的直线距离四舍五入后的值。
注:估算距离是可以自由设定的,并不局限于此处设定的,合理即可。
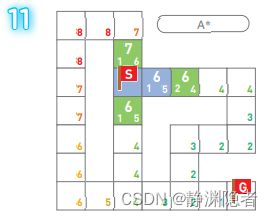
分别计算起点周围每个顶点的权重。计算方法 是“从起点到该顶点的距离”(方块左下)加上 “距离估算值”(方块右下)。
选择一个距离最小的顶点,用橙色表示。
将选择的顶点设为搜索完毕状态。
计算搜索完毕的顶点到下一个顶点的距离。
选择距离最短的一个顶点。
将选好的顶点设为搜索完毕状态。之后重复上述操作,直到到达终点为止。
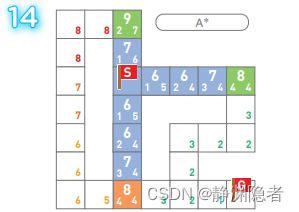
搜索中……
搜索完毕。非常容易看出,效率比前两者都高得多。
总的来说,这个搜索就只是增加了一个估算值,并将估算值加入距离而已。其余都与 狄克斯特拉算法 搜索相似。
三.需要注意
如果我们能得到一些启发信息,即各个顶点到终点的大致距离(这个距离不需是准确的值)我们就能使用 A* 算法。当然,有时这类信息是完全无法估算的,这时就不能 使用 A* 算法。
距离估算值越接近当前顶点到终点的实际值,A* 算法的搜索效率也就越高;反过 来,如果距离估算值与实际值相差较大,那么该算法的效率可能会比狄克斯特拉算法的 还要低。如果差距再大一些,甚至可能无法得到正确答案。
不过,当距离估算值小于实际距离时,是一定可以得到正确答案的(只是如果没有 设定合适的距离估算值,效率会变差)。
四.c++伪代码
再看伪代码前,我先定义几个字母。F表示距离与估算值的和,G表示估算值。
把起始格添加到 "开启列表"
do
{
寻找开启列表中F值最低的格子, 我们称它为当前格.
把当前格切换到关闭列表里.
for(遍历1-n个方向)
{
if (它不在开启列表中&&可行)
{
把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FG
if (用 G 值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
{
把这一格的上一步改成当前格, 并且重新计算这一格的 G、F 值.
}
}
}
}
while( 目标格已经在 "开启列表", 这时候路径被找到)
如果开启列表已经空了, 说明路径不存在.
最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径.很显然,这是狄克斯特拉算法的伪代码,唯一不同的就是G:估算值。
需要注意的是:此处用的是do-while循环。它是 while 循环的变体。在检查while()条件是否为真之前,该循环首先会执行一次do{}之内的语句,然后在while()内检查条件是否为真,如果条件为真的话,就会重复do...while这个循环,直至while()为假。
最后
祝大家元旦快乐,万事如意!
另:本文章同时收录于c++游戏专栏,标志着我开始写游戏制作笔记了!
我正在参加csdn博客之星评选活动,希望大佬点进链接点个五星评价,
https://bbs.csdn.net/topics/611389272?replyId=602251191&utm_medium=notify.im.community_cloud.1654e98c3c60c000.a&username=aliyonghang