备战秋招 | 笔试强训20
目录
一、选择题
二、编程题
三、选择题题解
四、编程题题解
一、选择题
1、对于顺序存储的线性表,访问结点和增加结点的时间复杂度为()。
A. O(n) O(n)
B. O(n) O(1)
C. O(1) O(n)
D. O(1) O(1)
2、在下列链表中不能从当前结点出发访问到其余各结点的是()
A. 双向链表 ‘
B. 单循环链表
C. 单链表
D. 双向循环链表
3、完成在双向循环链表结点 p 之后插入 s 的操作是()
A. p->next=s;s->prior=p;p->next->prior=s;s->next=p->next
B. p->next->prior=s;p->next=s;s->prior=p;s->next=p->next
C. s->prior=p;s->next=p->next;p->next=s;p->next->prior=s
D. s->prior=p;s->next=p->next;p->next->prior=s;p->next=s
4、栈是一种智能在某一端插入和删除的特殊线性表,它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,若6元素为A、B、C、D、E、F出栈顺序 为B、D、C、F、E、A,则S栈的最小容量为()。
A. 3
B. 4
C. 5
D. 6
5、现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为() (假设队头不存放数据)
A. (rear - front + N) % N + 1
B. (rear - front + N) % N
C. (rear - front) % (N + 1)
D. (rear - front + N) % (N - 1)
6、下述结论中,正确的是()①只有一个结点的二叉树的度为0;②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树
A. ①②③
B. ②③④
C. ②④
D. ①④
7、若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )
A. 0
B. 1
C. 2
D. 3
8、初始序列为1 8 6 2 5 4 7 3一组数采用堆排序,当建堆(小根堆)完毕时,堆所对应的二叉树中序遍历序列为()
A. 8 3 2 5 1 6 4 7
B. 3 2 8 5 1 4 6 7
C. 3 8 2 5 1 6 7 4
D. 8 2 3 5 1 4 7 6
9、解决散列法中出现冲突问题常采用的方法是()
A. 数字分析法、除余法、平方取中法
B. 数字分析法、除余法、线性探测法
C. 数字分析法、线性探测法、多重散列法
D. 线性探测法、多重散列法、链地址法
10、下列选项中,不可能是快速排序第2趟排序结果的是 ()
A. 2,3,5,4,6,7,9
B. 2,7,5,6,4,3,9
C. 3,2,5,4,7,6,9
D. 4,2,3,5,7,6,9
二、编程题
1、字符串反转 题目链接
2、公共子串计算 题目链接
三、选择题题解
1、对于顺序存储的线性表,访问结点和增加结点的时间复杂度为()。
A. O(n) O(n)
B. O(n) O(1)
C. O(1) O(n)
D. O(1) O(1)
正确答案:C
题解:
顺序存储的线性表支持随机访问,所以访问时间为O(1),而插入数据时,可能会出现挪动数据的现象,我们此时时间复杂度为O(N);
2、在下列链表中不能从当前结点出发访问到其余各结点的是()
A. 双向链表 ‘
B. 单循环链表
C. 单链表
D. 双向循环链表
正确答案:C
题解:
单链表无法访问结点前面的元素;
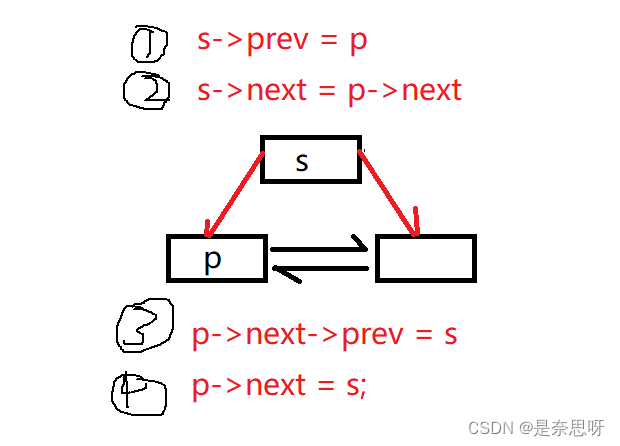
3、完成在双向循环链表结点 p 之后插入 s 的操作是()
A. p->next=s;s->prior=p;p->next->prior=s;s->next=p->next
B. p->next->prior=s;p->next=s;s->prior=p;s->next=p->next
C. s->prior=p;s->next=p->next;p->next=s;p->next->prior=s
D. s->prior=p;s->next=p->next;p->next->prior=s;p->next=s
正确答案:D
题解:
如下图所示,其中第一步与第二步能交换顺序,第三步与第四步不可;
4、栈是一种智能在某一端插入和删除的特殊线性表,它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,若6元素为A、B、C、D、E、F出栈顺序 为B、D、C、F、E、A,则S栈的最小容量为()。
A. 3
B. 4
C. 5
D. 6
正确答案:A
题解:
当出栈出到B时,我们不难想像,此时栈里最多存放AB两个元素,出到D时,表示出前栈内有ACD三个元素,接着出C,出到F时,之前肯定入了EF,栈内有AEF,接着出E,A;整个过程最多会有三个元素,故选A;
5、现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为() (假设队头不存放数据)
A. (rear - front + N) % N + 1
B. (rear - front + N) % N
C. (rear - front) % (N + 1)
D. (rear - front + N) % (N - 1)
正确答案:B
题解:
固定公式;
6、下述结论中,正确的是()①只有一个结点的二叉树的度为0;②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树
A. ①②③
B. ②③④
C. ②④
D. ①④
正确答案:D
题解:
所谓树的度只得是树中拥有最多子树的结点的子树数量,只有一个结点的二叉树,这个结点没有子树,故度为0,正确;二叉树的度不一定为2,也有可能为1或0,如①则是0,只有两个结点的二叉树的度为1;二叉树是一种有序树,无法交换两个左右子树位置;④正确;
7、若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )
A. 0
B. 1
C. 2
D. 3
正确答案:D
题解:
若把关键字依次插入平衡二叉树中,如下所示;题目问的是平衡因子为0的分支节点,故为3;
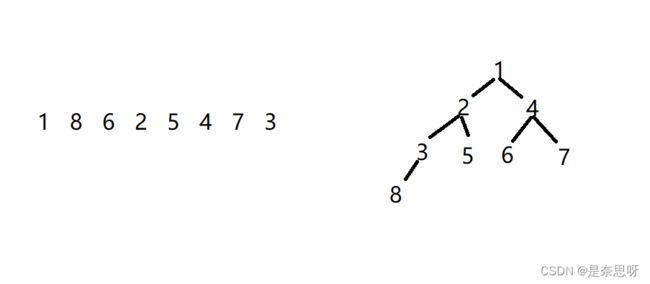
8、初始序列为1 8 6 2 5 4 7 3一组数采用堆排序,当建堆(小根堆)完毕时,堆所对应的二叉树中序遍历序列为()
A. 8 3 2 5 1 6 4 7
B. 3 2 8 5 1 4 6 7
C. 3 8 2 5 1 6 7 4
D. 8 2 3 5 1 4 7 6
正确答案:A
题解:
我们将上述序列模拟建堆如下图所示,故选A;
9、解决散列法中出现冲突问题常采用的方法是()
A. 数字分析法、除余法、平方取中法
B. 数字分析法、除余法、线性探测法
C. 数字分析法、线性探测法、多重散列法
D. 线性探测法、多重散列法、链地址法
正确答案:D
题解:
数字分析法、除余法、平方取中法等都属于哈希映射函数,并不是解决冲突的方法;只有D选项是解决冲突的方法;
10、下列选项中,不可能是快速排序第2趟排序结果的是 ()
A. 2,3,5,4,6,7,9
B. 2,7,5,6,4,3,9
C. 3,2,5,4,7,6,9
D. 4,2,3,5,7,6,9
正确答案:C
题解:
我们都知道快速排序每一趟都可以确定一个数字的位置,而C选项中,我们只能确定9在它自己的位置,故不可能是第2趟排序后的结果;
四、编程题题解
1、字符串反转
思路:我们可以用库中的reverse函数一步达成,但不建议,我们也可以通过两个下标,一个指向开始位置,一个指向最后一个字符的位置,依次交换;
#include
#include
using namespace std;
int main()
{
string str;
cin >> str;
int begin =0;
int end = str.size() -1;
while(begin < end)
{
swap(str[begin], str[end]);
begin++;
end--;
}
cout << str << endl;
return 0;
} 2、公共子串计算
思路:动态规划,这题不就是我们昨天那题的简化版么,可以移步下方链接;
题目解析
#include
#include
#include
using namespace std;
int main()
{
string str1, str2;
cin >> str1 >> str2;
int len1 = str1.size();
int len2 = str2.size();
int max = 0;
vector> dp(len1 + 1, vector(len2 + 1, 0));
for(int i = 1; i <= len1; i++)
{
for(int j = 1; j <= len2; j++)
{
if(str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
if(max < dp[i][j])
max = dp[i][j];
}
}
cout << max << endl;
return 0;
}