【Python机器学习】之 K-Means聚类算法

K-Means聚类

常见的聚类方法有：K-Means聚类、层次聚类、密度聚类、谱聚类和高斯混合聚类等。

1、K-Means聚类

1.1、K-Means聚类过程

​ K-Means 算法是一种无监督的聚类算法。K-Means核心思想是：给定的样本数据集，根据样本点之间的距离大小，把数据集划分成 K 个簇，并让簇内的样本点尽量距离近，而不同簇之间的距离极可能的远。

1.2、K-Means聚类过程

​ K-Means聚类过程有四个步骤，即聚类簇数K值的选择、K个聚类中心店的初始值选择、距离度量方式、损失函数的选择。

（1）聚类簇数 K 值的选择

​ 聚类簇数 K 值的选择是一个比较难处理的地方，它会对 K-Means 算法的最终结果起到关键作用，在实际中，一般并不知道要把样本数据分为几类。K-Means 算法在处理这个问题时注意依靠人工试探或者超参数探索的形式来确定。

（2）K 个聚类中心点初始值选择

​ K 个聚类中心点的初始值选择会直接的影响算法需要更新迭代的次数。K-Means 算法是先随机从样本点中选择 K 个点作为聚类中心点的初始值。（不是最好的方式，有改进方法）

（3）距离度量方式

​ 距离的计算有很多方式，如欧式距离、汉明距离等，使用较多的是欧式距离。假设数据样本点的特征维度是 N ，那么，两个 N 维向量$X=(x_{11},x_{12},...,x_{1n})$ 和 $Y=(y_{11},y_{12},...,y_{1n})$之间的欧式距离为：
$$d=\sqrt{\sum _{i=1}^N(x_{1i}-y_{1i})}$$

（4）损失函数的选择

​ 判断聚类迭代是否趋于稳定需要根据聚类损失函数的变化情况来判断。聚类算法的损失函数的各个簇中样本向量对应簇均值向量的均方误差。假设，数据样本点为$X=(x_1,x_2,...,x_n)$ ，需要被聚类成 K 个簇 $C=(c_1,c_2,...,c_n)$，则各个簇内样本点的均值向量为：
$${\mu }_k=\frac{1}{N_k}\sum _{x_i\in C_k}{x}_i$$
​ 其中，$N_k$为簇$C_k$中包含的样本点数目，所有簇的总均方误差为：
$$E=\sum _{k=1}^K\sum _{x_i\in C_k}||x_i-{\mu }_k|{|}^2$$
​ 所以，迭代求解 K-Means 算法的目标就是最小化损失函数，即均方误差。

1.3、K-Means算法步骤

输入：待聚类的数据集样本 $X=(x_1,x_2,...,x_n)$ ，聚类簇数K（即要分类数），最大迭代次数 n 。

输出：聚类后的数据集 $C=(c_1,c_2,...,c_n)$ 。

实现步骤：

1. 从数据集 $X$ 中随机选择 K 个聚类中心，设对应的向量为 $\mu =({\mu }_1,{\mu }_2,...,{\mu }_k)$ .
2. 计算各个样本点到 K 个聚类中心的距离 $||x_i-{\mu }_k|{|}_2^2$ ，并把各个样本点归入离其距离最近的类别中.
3. 重新进行迭代运算，计算得到的 K 个类别的中心向量，并更新为新的聚类中心，计算方法为：

$${\mu }_k^{‘}=\frac{1}{N_k}\sum _{x_i\in C_k}{x}_i$$

4. 重复第2和第3步计算，直到满足最大迭代次数n或所有类别的中心点不在发生变化，这时，得到聚类好的输出数据集 $C=(c_1,c_2,...,c_n)$.

2、K-Means 实践

2.1、简单K-Means

数据内容（部分）：

# 提取字段并可视化数据，使用scatter plot
f1 = data['V1'].values
f2 = data['V2'].values
#X = np.array(list(zip(f1, f2)))
X = np.random.random((200, 2))*10
plt.scatter(X[:,0], X[:,1], c='black', s=6)

#plt.scatter(f1, f2, c='black', s=8)

原始数据图像：

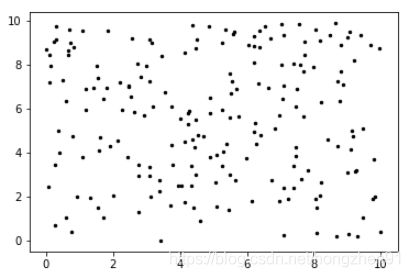
# K-means里的K值
k = 3
# 随机初始化K个中心点，把结果存储在C
C_x = np.random.randint(0, np.max(X), size=k)
C_y = np.random.randint(0, np.max(X), size=k)
C = np.array(list(zip(C_x, C_y)), dtype=np.float32)

print("初始化之后的中心点：")
print(C)

# 把中心点也展示一下
plt.scatter(X[:,0], X[:,1], c='#050505', s=7)
plt.scatter(C[:,0], C[:,1], marker='*', s=300, c='g')

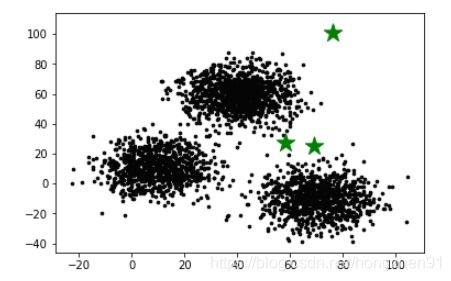
# 存储之前的中心点
C_old = np.zeros(C.shape)
clusters = np.zeros(len(X)) # K=3,  clusters = [0,0,1,2,1,0]

def dist(a, b, ax=1):
    return np.linalg.norm(a - b, axis=ax)

error = dist(C, C_old, None)
# 循环算法，直到收敛。收敛的条件就是，判断当前的中心点与之前的中心点之间有没有变化，没有变化距离就会变成0，然后抛出异常
while error != 0:
    # Assigning each value to its closest cluster
    for i in range(len(X)):
        distances = dist(X[i], C)
        cluster = np.argmin(distances)
        clusters[i] = cluster
    # 在计算新的中心点之前，先把旧的中心点存下来，以便计算距离
    C_old = deepcopy(C)
    # 计算新的中心点
    for i in range(k):
        points = [X[j] for j in range(len(X)) if clusters[j] == i]
        C[i] = np.mean(points, axis=0)
    error = dist(C, C_old, None)

colors = ['r', 'g', 'b', 'y', 'c', 'm']
fig, ax = plt.subplots()
for i in range(k):
        points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
        ax.scatter(points[:, 0], points[:, 1], s=7, c=colors[i])
ax.scatter(C[:, 0], C[:, 1], marker='*', s=200, c='#050505')

最终聚类结果：

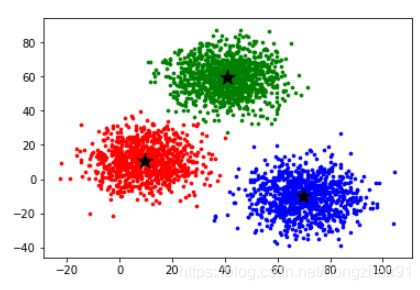
2.2、K-Means 用户分层

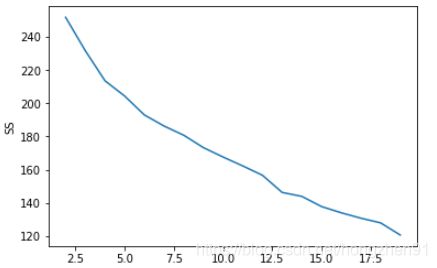
选择 K: The Elbow Sum-of-Squares Method
$$SS=\sum _k\sum _{x_i\in C_k}{\left(x_i-{\mu }_k\right)}^2$$

数据内容（部分）：

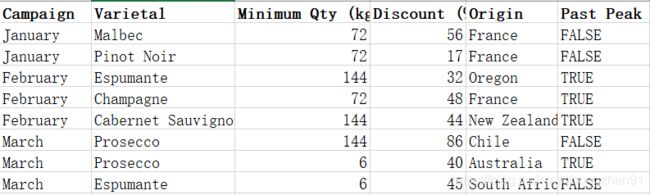
# 数据里包含了产品的信息，以及用户购买产品的记录
data_offer = pd.read_excel("./WineKMC.xlsx", sheetname=0)
data_offer.columns = ["offer_id", "campaign", "varietal", "min_qty", "discount", "origin", "past_peak"]

data_transactions = pd.read_excel("./WineKMC.xlsx", sheetname=1)
data_transactions.columns = ["customer_name", "offer_id"]
data_transactions['n'] = 1

# 合并两个dataframe
cust_compare = data_transactions.merge(data_offer, on = 'offer_id')

#Drop unnecessary columns
cust_compare = cust_compare.drop(['campaign', 'varietal', 'min_qty', 'discount', 'origin', 'past_peak'], axis = 1)

#Create pivot table
table = pd.pivot_table(cust_compare,  index = 'customer_name', columns = 'offer_id', aggfunc=np.sum, fill_value = 0)
table

SS = []
from sklearn.cluster import KMeans
for K in range(2, 20):
    kmeans = KMeans(n_clusters = K).fit(table) #Using all default values from method
    SS.append(kmeans.inertia_)
    
plt.plot(range(2,20), SS);
plt.xlabel('K');
plt.ylabel('SS');

#Choosing K=5
kmeans_5 = KMeans(n_clusters = 5).fit_predict(table)
points = list(kmeans_5)
d = {x:points.count(x) for x in points}
heights = list(d.values())
plt.bar(range(5),heights)
plt.xlabel('Clusters')
plt.ylabel('# of samples')

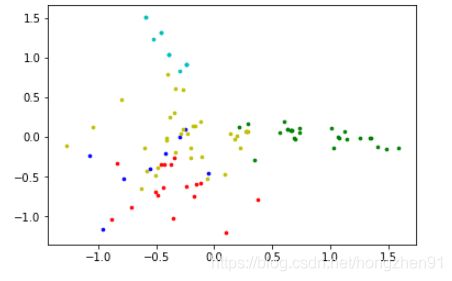
利用降维的方法来可视化样本

from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
data_new = pca.fit_transform(table)

print(table.shape)
print(data_new.shape)

colors = ['r', 'g', 'b', 'y', 'c', 'm']
fig, ax = plt.subplots()

for i in range(5):
        points = np.array([data_new[j] for j in range(len(data_new)) if kmeans_5[j] == i])
        ax.scatter(points[:, 0], points[:, 1], s=7, c=colors[i])

可视化数据：

3、K-Means总结

3.1、优点

（1）原理简单，容易实现，收敛速度较快，可解释性较强；

（2）需要调节的参数较少，主要的参数是聚类的类数 K，且聚类效果较好。

3.2、缺点

（1）聚类的类数 K值的选择不好控制，一般只能通过暴力搜索的方法来确定；

（2）只适合簇型的数据，对其他类型的数据聚类效果一般；

（3）当数据类别严重不平衡时，聚类效果也不理想；

（4）当数据量较大时，计算量也随之增大，采用Mini Batch K-Means的方法可以缓解，但是会牺牲准确度。

3.3、K-Means 和 KNN

​ K-Means 和 KNN 中的 K 的含义不同：

（1）K-Means 中的 K指的是聚类后的类别数目；

（2）KNN 中的 K指的是与待分类样本点距离最近的K个样本点。

确定；

（2）只适合簇型的数据，对其他类型的数据聚类效果一般；

（3）当数据类别严重不平衡时，聚类效果也不理想；

（4）当数据量较大时，计算量也随之增大，采用Mini Batch K-Means的方法可以缓解，但是会牺牲准确度。

3.3、K-Means 和 KNN

​ K-Means 和 KNN 中的 K 的含义不同：

（1）K-Means 中的 K指的是聚类后的类别数目；

（2）KNN 中的 K指的是与待分类样本点距离最近的K个样本点。

---

文中实例及参考：

• 刘宇波老师《Python入门机器学习》
• 《机器学习基础》
• 贪心学院，https://www.greedyai.com

---