【LeetCode Book】图解算法数据结构(更新中)
前言
个人整理的LeetCode Book 《图解算法数据结构》的笔记,用于后续复习。
作者:Krahets
链接:《图解数据结构与算法》
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
01 概述
算法复杂度
算法复杂度的两个角度:
- 时间复杂度: 假设各操作的运行时间为固定常数,统计算法运行的「计算操作的数量」 ,以代表算法运行所需时间;
- 空间复杂度: 统计在最差情况下,算法运行所需使用的「最大空间」。
问题的规模 N N N :
- 排序算法: N N N 代表需要排序的元素数量;
- 搜索算法: N N N 代表搜索范围的元素总和。
时间复杂度
时间复杂度具有「最差」、「平均」、「最佳」三种情况,分别使用 O O O , Θ \Theta Θ , Ω \Omega Ω 三种符号表示, O O O 是最常使用的时间复杂度评价符号。
根据从大到小排序,常见的算法时间复杂度主要有:
O ( 1 ) < O ( log N ) < O ( N ) < O ( N log N ) < O ( N 2 ) < O ( 2 N ) < O ( N ! ) O(1) < O(\text{log}N) < O(N) < O(N\text{log}N) < O(N^2) < O(2^N) < O(N!) O(1)<O(logN)<O(N)<O(NlogN)<O(N2)<O(2N)<O(N!)

示例:
O ( N 2 ) O(N^2) O(N2) :冒泡排序
O ( N log N ) O(N\text{log}N) O(NlogN):快速排序、归并排序、堆排序
空间复杂度
对于算法的性能,需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性,即时间和空间复杂度皆较低。而实际上,对于某个算法问题,同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度,往往是以提升空间复杂度为代价的,反之亦然。
由于当代计算机的内存充足,通常情况下,算法设计中一般会采取「空间换时间」的做法,即牺牲部分计算机存储空间,来提升算法的运行速度。
本文不对空间复杂度进行介绍,详见:《图解算法数据结构》空间复杂度
02 数据结构
数据结构简介
引言
数据结构是为实现对计算机数据有效使用的各种数据组织形式,服务于各类计算机操作。不同的数据结构具有各自对应的适用场景,旨在降低各种算法计算的时间与空间复杂度,达到最佳的任务执行效率。
如下图所示,常见的数据结构可分为「线性数据结构」与「非线性数据结构」,具体为:「数组」、「链表」、「栈」、「队列」、「树」、「图」、「散列表」、「堆」。
数组
数组是将相同类型的元素存储于连续内存空间的数据结构,其长度不可变。
如下图所示,构建此数组需要在初始化时给定长度,并对数组每个索引元素赋值,两种赋值方式:
// 1)
// 初始化一个长度为 5 的数组 array
int array[5];
// 元素赋值
array[0] = 2;
array[1] = 3;
array[2] = 1;
array[3] = 0;
array[4] = 2;
// 2)
int array[] = {2, 3, 1, 0, 2};

「可变数组」是经常使用的数据结构,其基于数组和扩容机制实现,相比普通数组更加灵活。常用操作有:访问元素、添加元素、删除元素。
链表
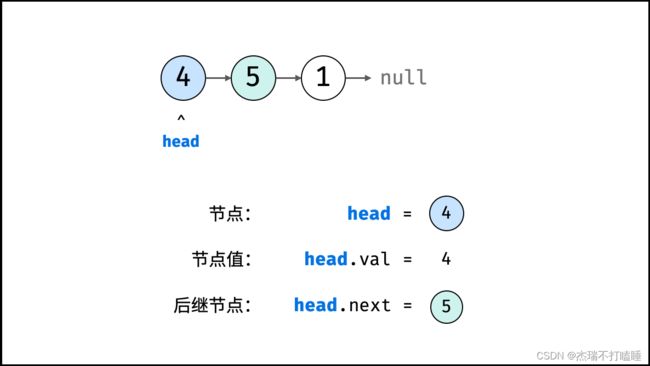
链表以节点为单位,每个元素都是一个独立对象,在内存空间的存储是非连续的。链表的节点对象具有两个成员变量:「值 val」,「后继节点引用 next」 。
struct ListNode {
int val; // 节点值
ListNode *next; // 后继节点引用
ListNode(int x) : val(x), next(NULL) {}
};
如下图所示,建立此链表需要实例化每个节点,并构建各节点的引用指向。
// 实例化节点
ListNode *n1 = new ListNode(4); // 节点 head
ListNode *n2 = new ListNode(5);
ListNode *n3 = new ListNode(1);
// 构建引用指向
n1->next = n2;
n2->next = n3;
栈
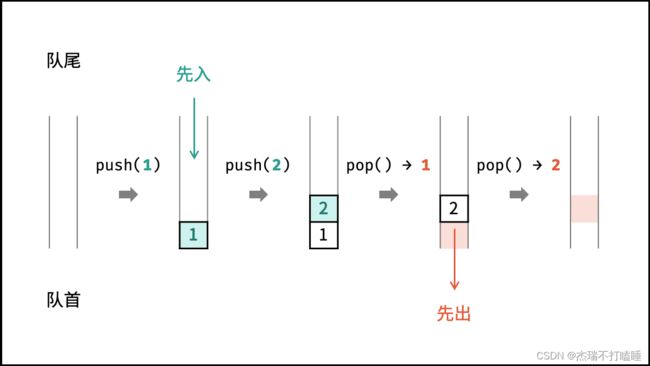
栈是一种具有 「先入后出」 特点的抽象数据结构,可使用数组或链表实现。
如下图所示,通过常用操作「入栈 push()」,「出栈 pop()」,展示了栈的先入后出特性。
stack<int> stk;
stk.push(1); // 元素 1 入栈
stk.push(2); // 元素 2 入栈
stk.pop(); // 出栈 -> 元素 2
stk.pop(); // 出栈 -> 元素 1
队列
队列是一种具有 「先入先出」 特点的抽象数据结构,可使用链表实现。
queue<int> que;
如下图所示,通过常用操作「入队 push()」,「出队 pop()」,展示了队列的先入先出特性。
que.push(1); // 元素 1 入队
que.push(2); // 元素 2 入队
que.pop(); // 出队 -> 元素 1
que.pop(); // 出队 -> 元素 2
树
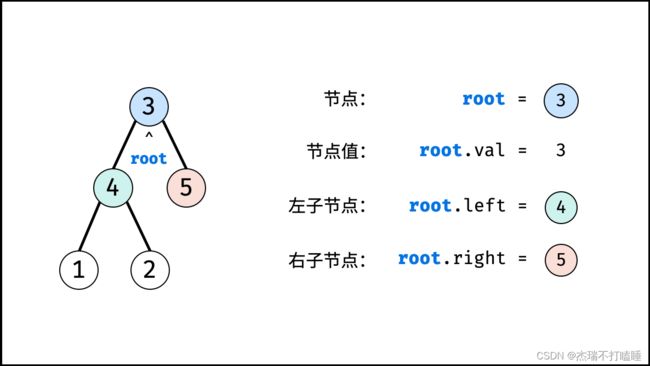
树是一种非线性数据结构,根据子节点数量可分为 「二叉树」 和 「多叉树」,最顶层的节点称为「根节点 root」。以二叉树为例,每个节点包含三个成员变量:「值 val」、「左子节点 left」、「右子节点 right」 。
struct TreeNode {
int val; // 节点值
TreeNode *left; // 左子节点
TreeNode *right; // 右子节点
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
如下图所示,建立此二叉树需要实例化每个节点,并构建各节点的引用指向。
// 初始化节点
TreeNode *n1 = new TreeNode(3); // 根节点 root
TreeNode *n2 = new TreeNode(4);
TreeNode *n3 = new TreeNode(5);
TreeNode *n4 = new TreeNode(1);
TreeNode *n5 = new TreeNode(2);
// 构建引用指向
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;
图
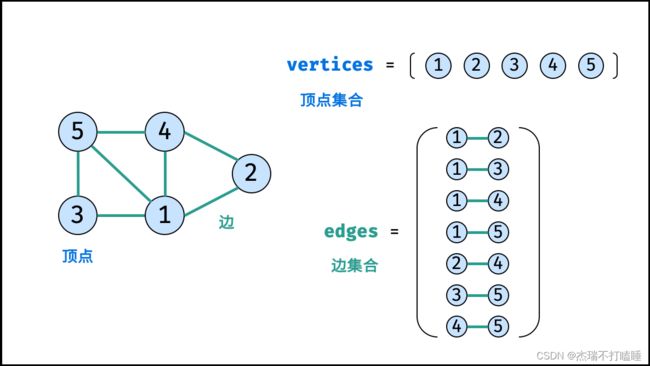
图是一种非线性数据结构,由 **「节点(顶点)vertex」**和「边 edge」组成,每条边连接一对顶点。根据边的方向有无,图可分为「有向图」和「无向图」。本文 以无向图为例 开展介绍。
如下图所示,此无向图的 顶点 和 边 集合分别为:
- 顶点集合:
vertices = {1,2.3,4,5} - 边集合:
edges = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (3, 5), (4, 5)}
- 邻接矩阵
int vertices[5] = {1, 2, 3, 4, 5};
int edges[5][5] = {{0, 1, 1, 1, 1},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{1, 1, 0, 0, 1},
{1, 0, 1, 1, 0}};
- 邻接表
int vertices[5] = {1, 2, 3, 4, 5};
vector<vector<int>> edges;
vector<int> edge_1 = {1, 2, 3, 4};
vector<int> edge_2 = {0, 3};
vector<int> edge_3 = {0, 4};
vector<int> edge_4 = {0, 1, 4};
vector<int> edge_5 = {0, 2, 3};
edges.push_back(edge_1);
edges.push_back(edge_2);
edges.push_back(edge_3);
edges.push_back(edge_4);
edges.push_back(edge_5);
Note
邻接矩阵 VS 邻接表 :
邻接矩阵的大小只与节点数量有关,即 N 2 N^2 N2 ,其中 N N N 为节点数量。因此,当边数量明显少于节点数量时,使用邻接矩阵存储图会造成较大的内存浪费。
因此,邻接表适合存储稀疏图(顶点较多、边较少); 邻接矩阵适合存储稠密图(顶点较少、边较多)。
散列表
散列表是一种非线性数据结构,通过利用 Hash 函数将指定的「键 key」映射至对应的「值 value」,以实现高效的元素查找。
例:可通过建立姓名为 key ,学号为 value 的散列表实现从「姓名」查找「学号」,代码如下:
// 初始化散列表
unordered_map<string, int> dic;
// 添加 key -> value 键值对
dic["小力"] = 10001;
dic["小特"] = 10002;
dic["小扣"] = 10003;
// 从姓名查找学号
dic.find("小力")->second; // -> 10001
dic.find("小特")->second; // -> 10002
dic.find("小扣")->second; // -> 10003
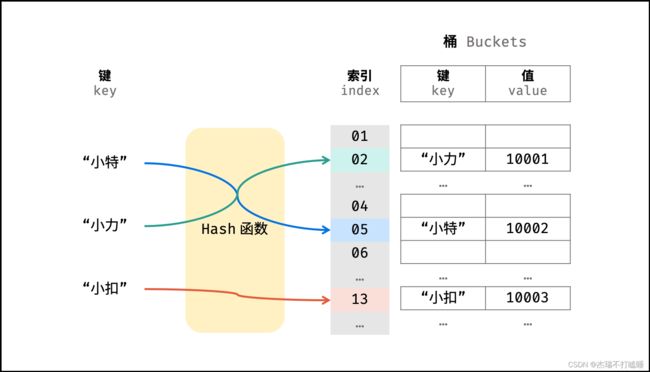
Hash 函数需保证 低碰撞率 、 高鲁棒性 等,以适用于各类数据和场景。
堆
堆是一种基于 「完全二叉树」 的数据结构,可使用数组实现。以堆为原理的排序算法称为「堆排序」,基于堆实现的数据结构为「优先队列」。堆分为「大顶堆」和「小顶堆」,大(小)顶堆:任意节点的值不大于(小于)其父节点的值。
完全二叉树定义: 设二叉树深度为 k k k ,若二叉树除第 k k k 层外的其它各层(第 1 1 1 至 k − 1 k−1 k−1 层)的节点达到最大个数,且处于第 k k k 层的节点都连续集中在最左边,则称此二叉树为完全二叉树。
如下图所示,为包含 1, 4, 2, 6, 8 元素的小顶堆。将堆(完全二叉树)中的结点按层编号,即可映射到右边的数组存储形式。
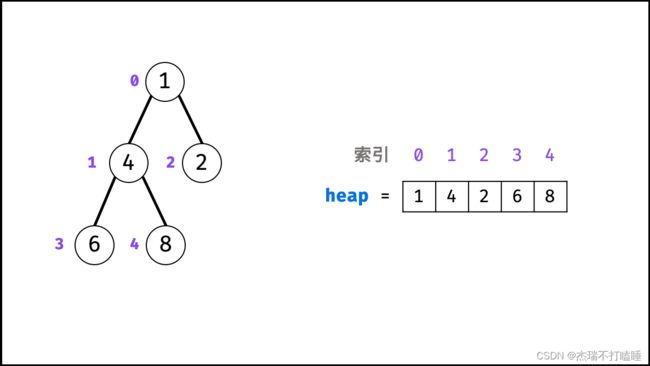
通过使用「优先队列」的「压入 push()」和「弹出 pop()」操作,即可完成堆排序,实现代码如下:
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> heap;
// 元素入堆
heap.push(1);
heap.push(4);
heap.push(2);
heap.push(6);
heap.push(8);
// 元素出堆(从小到大)
heap.pop(); // -> 1
heap.pop(); // -> 2
heap.pop(); // -> 4
heap.pop(); // -> 6
heap.pop(); // -> 8
Note
堆是一种非线性结构,可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组,但堆并不一定是完全二叉树。
普通树占用的内存空间比它们存储的数据要多。普通树必须为节点对象以及左/右子节点指针分配额外的内存。堆仅仅使用数组,且不使用指针。
参考:堆排序
题目
剑指 Offer 09. 用两个栈实现队列
思路:
使用两个栈A、B维护队列。A维护队尾部分,A.top() 存放队尾元素;B维护队首部分,B.top() 存放队首元素。
- 队列尾部插入整数时,只操作队尾,直接将整数压入
A; - 队列头部删除整数时,分以下几种情况:
B不为空,直接返回队尾整数;B为空:
1)A也为空,说明整个队列为空,返回-1;
2)A不为空,将A压入B,再返回队尾元素。
由于A、B将整个队列分为队尾和队首两个互不影响的部分,在删除数据后,不需要再将B中的数据还原到A中。
代码:
class CQueue {
public:
stack<int> stk; // stk.top()存放队尾元素
stack<int> stk_r; // stk_r.top()存放队首元素
CQueue() { }
void appendTail(int value) {
stk.push(value);//直接压入stk
}
int deleteHead() {
// 1. stk_r不为空,直接弹栈
// 2. stk_r为空
// 1) stk不为空,将stk压入stk_r,再弹栈
// 2) stk为空,返回 -1
if(stk_r.empty()) {
if(stk.empty()) {
return -1;
} else {
while(!stk.empty()) {
stk_r.push(stk.top());
stk.pop();
}
}
}
int res = stk_r.top();
stk_r.pop();
return res;
}
};
/**
* Your CQueue object will be instantiated and called as such:
* CQueue* obj = new CQueue();
* obj->appendTail(value);
* int param_2 = obj->deleteHead();
*/
剑指 Offer 30. 包含 min 函数的栈
思路:
普通栈的 push() 和 pop() 函数的复杂度为 O ( 1 ) O(1) O(1) ;而获取栈最小值 min() 函数需要遍历整个栈,复杂度为 O ( N ) O(N) O(N) 。
本题难点: 将 min() 函数复杂度降为 O ( 1 ) O(1) O(1) 。可借助辅助栈实现:
- 数据栈
A: 栈A用于存储所有元素; - 辅助栈
B: 栈B中存储栈A中所有 非严格降序 元素的子序列,则栈A中的最小元素始终对应栈B的栈顶元素。此时,min()函数只需返回栈 B 的栈顶元素即可。
因此,只需设法维护好栈 B 的元素,使其保持是栈 A 的非严格降序元素的子序列,即可实现 min() 函数的 O ( 1 ) O(1) O(1) 复杂度。
代码:
class MinStack {
public:
/** initialize your data structure here. */
stack<int> A;
//如果只用int保存min,在pop时min无法维护
stack<int> A_min; //辅助栈,存放A中所有非严格降序元素的子序列
MinStack() {}
void push(int x) {
A.push(x);
if(A_min.empty() || A_min.top() >= x) {
A_min.push(x);
}
}
void pop() {
if(A.top() == A_min.top()) {
A_min.pop();
}
A.pop();
}
int top() {
return A.top();
}
int min() {
return A_min.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->min();
*/
剑指 Offer 06. 从尾到头打印链表
思路:
简单的链表操作,不推荐使用insert(),效率低。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
// class Solution {
// public:
// vector reversePrint(ListNode* head) {
// ListNode* point = head;
// vector res;
// while(point != NULL) {
// res.insert(res.begin(),point->val); //insert效率低
// point = point -> next;
// }
// return res;
// }
// };
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
ListNode* point = head;
int n = 0;
while(point != NULL) {
n ++;
point = point -> next;
}
vector<int> res(n);
// point = head;
while(head != NULL) {
res[n-1] = head -> val;
head = head -> next;
n--;
}
return res;
}
};
剑指 Offer 24. 反转链表
思路:
遍历源链表,并插入目标链表的头部。
上面的解法需要新建链表,空间复杂度为 O ( N ) O(N) O(N) 。LeetCode官方题解思路:
在遍历链表时,将当前节点的 next \textit{next} next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
// 1) My Solution
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* point = head;
ListNode* res = NULL;
while(point != NULL) {
ListNode* myNode = new ListNode(point -> val);
myNode -> next = res;
point = point -> next;
res = myNode;
}
return res;
}
};
// 2) LeetCode-Solution
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* curr = head;
while (curr) {
ListNode* next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};
剑指 Offer 35. 复杂链表的复制
本题难点: 在复制链表的过程中构建新链表各节点的 random 引用指向。
思路:
先新建节点,并构建原节点到新节点的map,再根据该map构建新链表的random指向。
代码:
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
Node* copyRandomList(Node* head) {
map<Node* , Node*> tmp;
Node* point = head;
Node* cur;
//复制节点
while(point != NULL) {
cur = new Node(point -> val);
tmp[point] = cur;
point = point -> next;
}
//构建新链表的 next 和 random 指向
point = head;
while(point != NULL) {
tmp[point] -> next = tmp[point->next];
tmp[point] -> random = tmp[point->random];
point = point -> next;
}
return tmp[head];
}
};
剑指 Offer 05. 替换空格
代码:
class Solution {
public:
string replaceSpace(string s) {
string res = "";
for(int i = 0; i < s.length(); i ++) {
if(s[i] == ' ') {
res.append("%20");
} else {
res.append(1,s[i]);
}
}
return res;
}
};
剑指 Offer 58 - II. 左旋转字符串
思路:
将 [ 0 , n − 1 ] [0,n-1] [0,n−1] 的串拼接到 [ n , end ] [n,\text{end}] [n,end] 之后。
代码:
class Solution {
public:
string reverseLeftWords(string s, int n) {
string res = s.substr(n); // s.substr(index, num_size);
res.append(s.substr(0,n));
return res;
}
};
03 动态规划
动态规划简介
参考链接:看一遍就理解:动态规划详解
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。
例如,斐波那契数列问题可以使用 暴力递归、记忆化递归和动态规划 三种解法。
- 暴力递归存在大量重复计算,效率低下;
- 记忆化递归在递归中第一次求解子问题时,就将子问题的解保存,后续递归中再次遇到相同子问题时,直接访问内存赋值;
- 递归本质上是基于分治思想的自顶向下的解法。借助记忆化递归思想,可应用动态规划自底向上求解。
动态规划的解题套路
动态规划适用的问题:
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
比如一些求最值的场景,如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景。
动态规划解题框架:
若确定给定问题具有重叠子问题和最优子结构,那么就可以使用动态规划求解。总体上看,求解可分为四步:
- 状态定义: 构建问题最优解模型,包括问题最优解的定义、有哪些计算解的自变量;
- 初始状态: 确定基础子问题的解(即已知解),原问题和子问题的解都是以基础子问题的解为起始点,在迭代计算中得到的;
- 转移方程: 确定原问题的解与子问题的解之间的关系是什么,以及使用何种选择规则从子问题最优解组合中选出原问题最优解;
- 返回值: 确定应返回的问题的解是什么,即动态规划在何处停止迭代。
题目
剑指 Offer 10- I. 斐波那契数列
代码:
class Solution {
public:
int fib(int n) {
if(n <= 1) return n;
int res = 0; //n
int a = 0; // n-2
int b = 1; // n-1
for(int i = 2; i <= n; i++) {
res = (a + b) % 1000000007;
a = b;
b = res;
}
return res;
}
};
剑指 Offer 10- II. 青蛙跳台阶问题
思路:青蛙跳到第n阶的最后一步有两种方法:1)从(n-1)阶跳1级;2)从(n-2)阶跳2级。因此,状态转移方程为 f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n)= f(n-1)+f(n-2) f(n)=f(n−1)+f(n−2)。
代码:
class Solution {
public:
int numWays(int n) {
if(n <= 1) return 1;
// 最后一步到第n阶台阶有两种方法,从(n-1)跳
// 状态转移方程 f(n) = f(n-1) + f(n-2)
int a = 1, b = 1, res;
for(int i = 2; i <= n; i ++) {
res = (a + b) % 1000000007;
a = b;
b = res;
}
return res;
}
};
剑指 Offer 63. 股票的最大利润
思路:遍历股票价格,当前最大利润为
当 前 股 票 价 格 − 当 前 最 低 股 票 价 格 当前股票价格- 当前最低股票价格 当前股票价格−当前最低股票价格
记录最大利润。
代码:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if(n <= 1) return 0;
int buy = prices[0];
int profit = 0;
for(int i = 1; i < n; i ++) {
if(prices[i] < buy) { // 选择在股票最低价时购入
buy = prices[i];
}
profit = max(profit, prices[i] - buy);
}
return profit;
}
};
剑指 Offer 42. 连续子数组的最大和
思路:令以 n u m s [ i ] nums[i] nums[i] 结尾的连续子数组的最大和为 f [ i ] f[i] f[i],则该题的解为:
max { f [ i ] } i = 0 n − 1 \max \{f[i]\}_{i=0}^{n-1} max{f[i]}i=0n−1
若 f [ i − 1 ] < 0 f[i-1] < 0 f[i−1]<0,则 f [ i − 1 ] + n u m s [ i ] < n u m s [ i ] f[i-1] + nums[i]< nums[i] f[i−1]+nums[i]<nums[i],所以状态转移方程为:
f [ i ] = { f [ i − 1 ] + n u m s [ i ] f [ i − 1 ] > 0 n u m s [ i ] f [ i − 1 ] ≤ 0 f[i]=\left\{ \begin{array}{ccl} f[i-1] + nums[i] & & {f[i-1]>0}\\ nums[i] & & {f[i-1] \leq 0} \end{array} \right. f[i]={f[i−1]+nums[i]nums[i]f[i−1]>0f[i−1]≤0
代码:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
if(n == 1) return nums[0];
int sum = nums[0];
int ans = sum;
for(int i = 1; i < n; i ++) {
if(sum <= 0) { // 若 当前sum < 0,说明 sum 对最大累加和没有贡献
sum = nums[i];
} else {
sum = sum + nums[i];
}
ans = max(ans, sum);
}
return ans;
}
};
剑指 Offer 47. 礼物的最大价值
思路:记录每个网格点可以拿到最多的礼物价值 v a l u e value value,网格点 [ i ] [ j ] [i][j] [i][j] 只能从 [ i − 1 ] [ j ] [i-1][j] [i−1][j] 或者 [ i ] [ j − 1 ] [i][j-1] [i][j−1] 到达即 v a l u e [ i ] [ j ] value[i][j] value[i][j] 只与 $value[i-1][j] $和 v a l u e [ i ] [ j − 1 ] value[i][j-1] value[i][j−1] 有关。状态转移方程为:
v a l u e [ i ] [ j ] = m a x ( v a l u e [ i − 1 ] [ j ] , v a l u e [ i ] [ j − 1 ] ) + g r i d [ i ] [ j ] value[i][j] = max(value[i-1][j], value[i][j-1]) + grid[i][j] value[i][j]=max(value[i−1][j],value[i][j−1])+grid[i][j]
代码:
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
int value[m][n]; // 记录每个网格点可以拿到最多的礼物价值
// 网格点[i][j] 只能从 [i-1][j] 或者 [i][j-1] 到达
// 即 value[i][j] 只与 value[i-1][j] 和 value[i][j-1] 有关
// 初始化边界
value[0][0] = grid[0][0];
for(int i = 1; i < m; i ++) {
value[i][0] = value[i-1][0] + grid[i][0];
}
for(int j = 1; j < n; j ++) {
value[0][j] = value[0][j-1] + grid[0][j];
}
for(int i = 1; i < m; i ++) {
for(int j = 1; j < n; j ++) {
value[i][j] = max(value[i-1][j], value[i][j-1]) + grid[i][j];
}
}
return value[m-1][n-1];
}
};
Note:可以直接修改 g r i d grid grid 记录礼物的最大价值。
剑指 Offer 46. 把数字翻译成字符串
代码:
class Solution {
public:
int translateNum(int num) {
string s = to_string(num);
int a = 1, b = 1, len = s.size();
for(int i = len - 2; i > -1; i--) {
string tmp = s.substr(i, 2);
int c = tmp.compare("10") >= 0 && tmp.compare("25") <= 0 ? a + b : a;
b = a;
a = c;
}
return a;
}
};
剑指 Offer 48. 最长不含重复字符的子字符串
思路:滑动窗口
代码:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.length();
if(n <= 1) return n;
int l = 0, r = 0;
unordered_map<char,bool> flag;
int res = 0;
while(r < n) {
if(!flag[s[r]]) { // 未重复
res = max(res, r - l + 1);
flag[s[r]] = true; // 先修改状态在移动指针
r ++; // 右指针右移
} else {
flag[s[l]] = false;
l ++;
}
}
return res;
}
};
04 搜索与回溯算法
题目
剑指 Offer 32 - I. 从上到下打印二叉树
思路:二叉树的层次遍历(BFS),使用队列实现。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if(root == NULL) return res;
que.push(root);
while(!que.empty()) { //遍历队列
TreeNode* curNode = que.front();
que.pop();
res.push_back(curNode->val);
if(curNode->left != NULL) que.push(curNode->left);
if(curNode->right != NULL) que.push(curNode->right);
}
return res;
}
};
剑指 Offer 32 - II. 从上到下打印二叉树 II
思路:还是二叉树的层次遍历。用 queue 存放每层节点。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
queue<queue<TreeNode*>> Que;
queue<TreeNode*> q;
if(root == NULL) return res;
q.push(root);
Que.push(q);
while(!Que.empty()) {
queue<TreeNode*> que = Que.front(); // 该层节点
Que.pop();
vector<int> row;// 存放该层val
queue<TreeNode*> quenextlevel; // 下一层节点
while(!que.empty()) {
TreeNode* curNode = que.front();
que.pop();
row.push_back(curNode->val);
if(curNode->left != NULL) quenextlevel.push(curNode->left);
if(curNode->right != NULL) quenextlevel.push(curNode->right);
}
if(!quenextlevel.empty()) Que.push(quenextlevel);
res.push_back(row);
}
return res;
}
};
其实每次进入第一层循环时,queue的长度即为该层的节点数。
题解代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
int cnt = 0;
if(root != NULL) que.push(root);
while(!que.empty()) {
vector<int> tmp;
for(int i = que.size(); i > 0; --i) {
root = que.front();
que.pop();
tmp.push_back(root->val);
if(root->left != NULL) que.push(root->left);
if(root->right != NULL) que.push(root->right);
}
res.push_back(tmp);
}
return res;
}
};
剑指 Offer 32 - III. 从上到下打印二叉树 III
思路:参考上一题,分奇偶层打印。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if(root == NULL) return res;
que.push(root);
bool flag = true;
while(!que.empty()) {
int nodeNum = que.size();
vector<int> tmp(nodeNum);
if (flag) {
for(int i = 0; i < nodeNum; i ++) {
TreeNode* curNode = que.front();
que.pop();
tmp[i] = curNode->val;
if(curNode->left != NULL) que.push(curNode->left);
if(curNode->right != NULL) que.push(curNode->right);
}
} else {
for(int i = nodeNum-1; i >= 0 ; i --) {
TreeNode* curNode = que.front();
que.pop();
tmp[i] = curNode->val;
if(curNode->left != NULL) que.push(curNode->left);
if(curNode->right != NULL) que.push(curNode->right);
}
}
flag = !flag;
res.push_back(tmp);
}
return res;
}
};
剑指 Offer 26. 树的子结构
思路:
遍历 A 树的每个节点 node ,判断以 node 为 root 的子树是否包含树B。
若 A 或 B 为空树,根据题意,返回 false。
判断以 node 为 root 的子树是否包含树B时,
- 若搜索过程中树
B为空,说明匹配成功,返回true; - 若
A为空但B不为空,或者节点A与节点B的val不相等,则说明匹配失败,返回false; - 节点
A与节点B的val相等,递归,返回树A与树B的左右子树是否匹配。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool recur(TreeNode* A, TreeNode* B) {//判断以A为root的子树是否包含B
if(B == NULL) return true; //搜索过程中B为空,说明已经搜索完毕,返回true
if(A == NULL || A->val != B->val) return false;
return recur(A->left, B->left) && recur(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if(A == NULL || B == NULL) return false;
return (recur(A,B) || isSubStructure(A->left,B) || isSubStructure(A->right,B));
}
};
剑指 Offer 27. 二叉树的镜像
思路:遍历二叉树,修改指针,需要一个额外的指针暂存修改的指针。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(root == NULL) return root;
TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
if(root->left != NULL) mirrorTree(root->left);
if(root->right != NULL) mirrorTree(root->right);
return root;
}
};
剑指 Offer 28. 对称的二叉树
思路:递归,从上到下判断左右子树是否对称。注意,空树是对称的。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isMirrorTree(TreeNode* A, TreeNode* B) {
if(A == NULL && B == NULL) //均为空
return true;
if(A == NULL || B == NULL) // 只有一个为空
return false;
if(A->val != B->val) return false; //均不为空
return (isMirrorTree(A->left, B->right) && isMirrorTree(A->right, B->left));
}
bool isSymmetric(TreeNode* root) {
// if(root == NULL) return false;
if(root == NULL) return true;
return isMirrorTree(root->left, root->right);
}
};
剑指 Offer 12. 矩阵中的路径
代码:
class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
int m = board.size();
int n = board[0].size();
for(int i = 0; i < m; i ++) {
for (int j = 0; j < n; j ++) {
if(dfs(board,word,i,j,0)) return true;
}
}
return false;
}
bool dfs(vector<vector<char>>& board, string word, int i, int j, int k) {
int m = board.size();
int n = board[0].size();
if(i < 0 || i >= m || j < 0 || j >= n || board[i][j] != word[k]) return false;
if(k == word.length()-1) return true;
board[i][j] = '0';
bool res = dfs(board,word,i-1,j,k+1) || dfs(board,word,i+1,j,k+1) || dfs(board,word,i,j-1,k+1) || dfs(board,word,i,j+1,k+1);
board[i][j] = word[k];
return res;
}
};
05 分治算法
06 排序
07 查找算法
题目
剑指 Offer 03. 数组中重复的数字
思路:
先排序后遍历 。官方题解使用的哈希表,遍历数组,遇到重复的直接返回,时间复杂度为 O ( N ) O(N) O(N);
代码:
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
//先排序后遍历
sort(nums.begin(),nums.end());
for(int i = 0; i < nums.size()-1; i ++) {
if(nums[i] == nums[i+1]) {
return nums[i];
}
}
return 0;
}
};
剑指 Offer 53 - I. 在排序数组中查找数字 I
思路:
二分查找找到target位置,再向左向右计数。官方题解使用二分查找分别找到左边界 l e f t left left 和右边界 r i g h t right right,最后返回 r i g h t − l e f t right - left right−left。
代码:
class Solution {
public:
int search(vector<int>& nums, int target) {
//nums有序,二分查找找到target位置,再向左向右计数
int n = nums.size();
if(n == 0) return 0;
//二分查找
int l = 0;
int r = n - 1;
int idx = -1; // 查找到的target索引
while(l <= r) {
int mid = (l + r) / 2;
if(nums[mid] == target) {
idx = mid;
break;
} else if(nums[mid] < target) {
l = mid + 1;
} else {
r = mid - 1;
}
}
if(idx == -1) return 0;
int cnt = 1;
int i = idx;
while(i - 1 >= 0) { // 向左查找
if(nums[--i] == target) {
cnt ++;
} else {
break;
}
}
i = idx;
while(i + 1 < n) { // 向右查找
if(nums[++i] == target) {
cnt ++;
} else {
break;
}
}
return cnt;
}
};
Note:
大多数情况下,如果 l e f t left left 和 r i g h t right right 初始值都是有效的索引,就用 < = <= <= 。其实,简单来说就是 r i g h t right right 取 n u m s . l e n g t h − 1 nums.length - 1 nums.length−1, 这就可以 < = <= <= ,这时的 while 结束条件是 l e f t = r i g h t + 1 left = right + 1 left=right+1。
参考资料:二分查找边界问题总结
剑指 Offer 53 - II. 0~n-1中缺失的数字
思路:
二分查找第一个 n u m s [ i ] ≠ i nums[i] \neq i nums[i]=i 的数字。
代码:
class Solution {
public:
int missingNumber(vector<int>& nums) {
//二分查找第一个nums[i] != i 的数字
int n = nums.size();
if(n == 1 && nums [0] != 0) return 0;
int l = 0;
int r = n - 1;
while(l <= r) {
int mid = ((r - l) >> 1) + l;
if(nums[mid] == mid) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return l;
}
};
剑指 Offer 04. 二维数组中的查找
思路:
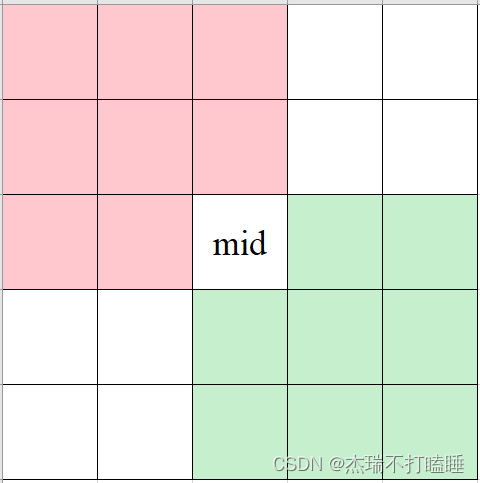
二分查找+递归。下图中红色部分为一定小于 m a t r i x [ r _ m i d ] [ c _ m i d ] matrix[r\_mid][c\_mid] matrix[r_mid][c_mid] 的元素,绿色部分为一定大于 m a t r i x [ r _ m i d ] [ c _ m i d ] matrix[r\_mid][c\_mid] matrix[r_mid][c_mid] 的元素。
二分查找的情况:
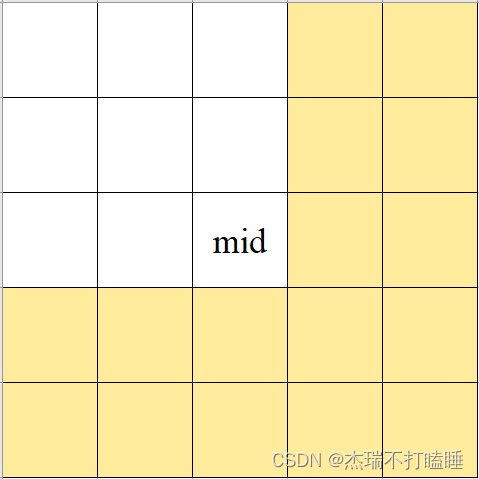
- m a t r i x [ r _ m i d ] [ c _ m i d ] < t a r g e t matrix[r\_mid][c\_mid] < target matrix[r_mid][c_mid]<target ,排除红色部分,需要查找的区域:
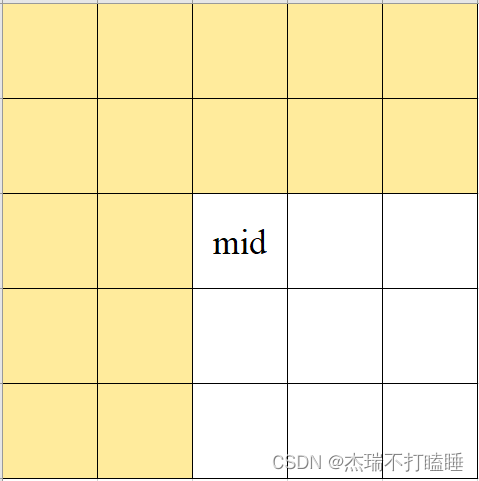
- m a t r i x [ r _ m i d ] [ c _ m i d ] > t a r g e t matrix[r\_mid][c\_mid] > target matrix[r_mid][c_mid]>target ,排除绿色部分,需要查找的区域:
代码:
class Solution {
public:
bool findNumber(vector<vector<int>>& matrix, int target, int rb, int re, int cb, int ce) {
if(rb > re || cb > ce) {
return false;
}
int r_mid = (rb + re) / 2;
int c_mid = (cb + ce) / 2;
if(matrix[r_mid][c_mid] == target) {// 找到
return true;
} else if (matrix[r_mid][c_mid] < target) { // 递归查找
return (findNumber(matrix,target,r_mid+1,re,cb,c_mid) || findNumber(matrix,target,rb,r_mid,c_mid+1,ce) || findNumber(matrix, target, r_mid+1,re,c_mid+1,ce));
} else {
return (findNumber(matrix,target,rb,r_mid-1,cb,c_mid-1) || findNumber(matrix,target,rb,r_mid-1,c_mid,ce) || findNumber(matrix, target, r_mid,re,cb,c_mid-1));
}
}
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
//第一反应是二分查找+递归
int n = matrix.size();
if(n == 0) return false;
int m = matrix[0].size();
if(m == 0) return false;
return findNumber(matrix, target, 0, n - 1, 0, m - 1);
}
};
剑指 Offer 11. 旋转数组的最小数字
思路:
二分查找,min一定在某组 [ l a r g e , s m a l l ] [large,small] [large,small] 之间。需要注意的地方写在代码注释里了。
我的代码:
class Solution {
public:
int minArray(vector<int>& numbers) {
//二分查找, 由于数组旋转过,min一定在某组[large,small]之间。
int l = 0;
int r = numbers.size() - 1;
while(l <= r) {//会进入死循环是因为某一次循环后边界值不再改变
int mid = (l + r) / 2; //除非l=r, 否则mid < r
if(numbers[l] > numbers[mid]) { //mid可能为最小值
r = mid; // mid < r, r = mid 一定会修改r的值,不会进入死循环
} else if (numbers[mid] > numbers[r]) { //mid不可能为最小值
//如果这里改成 l = mid,就可能会因为 l = r - 1, mid = l 而进入死循环
l = mid + 1;
} else {
//其他情况任意修改一边界值,为保证最后一轮循环 l = mid,这里选择修改r
r --;
}
}
// 出循环时 l 为最后一轮循环的 mid
return numbers[l];
}
};
剑指 Offer 50. 第一个只出现一次的字符
思路:哈希表。
代码:
class Solution {
public:
char firstUniqChar(string s) {
int n = s.length();
if(n == 0) return ' ';
if(n == 1) return s[0];
unordered_map<char, int> cnts;
for(char c : s) {
// char c = s[i];
if(cnts[c]) {
cnts[c] ++;
} else {
cnts[c] = 1;
}
}
for(char c : s) {
if(cnts[c] == 1) return c;
}
return ' ';
}
};
08 双指针
题目
剑指 Offer 18. 删除链表的节点
思路:保存前一节点。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head == NULL) return head;
if(head->val == val) return head->next;
ListNode* cur = head->next;
ListNode* prev = head;
while(cur != NULL){
if(cur->val == val ) {
prev->next = cur->next;
return head;
}
cur = cur->next;
prev = prev->next;
}
return head;
}
};
剑指 Offer 22. 链表中倒数第 k 个节点
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
int n = 0;
ListNode* p = head;
while(p != NULL) {
n ++;
p = p->next;
}
p = head;
while(p != NULL) {
if(n == k) return p;
n --;
p = p->next;
}
return NULL;
}
};
剑指 Offer 25. 合并两个排序的链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1 == NULL) return l2;
if(l2 == NULL) return l1;
ListNode* p1 = l1;
ListNode* p2 = l2;
ListNode* head = new ListNode(0);
ListNode* p = head;
while(p1 != NULL && p2 != NULL) {
if(p1->val <= p2->val) {
p->next = p1;
p1 = p1->next;
} else {
p->next = p2;
p2 = p2->next;
}
p = p->next;
if(p->next == NULL) {
p->next = p1 != NULL ? p1 : p2;
}
}
return head->next;
}
};
剑指 Offer 52. 两个链表的第一个公共节点
思路:我的思路是差值法,题解是将链表看成循环链表,同时移动两个指针。
我的代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *pA = headA;
ListNode *pB = headB;
int lenA = 0;
int lenB = 0;
while(pA != NULL) {
lenA ++;
pA = pA->next;
}
while(pB != NULL) {
lenB ++;
pB = pB->next;
}
pA = headA;
pB = headB;
if(lenA > lenB) {
for(int i = 0; i < lenA - lenB; i ++)
pA = pA->next;
} else {
for(int i = 0; i < lenB - lenA; i ++)
pB = pB->next;
}
while(pA != pB) {
pA = pA->next;
pB = pB->next;
}
return pA;
}
};
题解:
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *A = headA, *B = headB;
while (A != B) {
A = A != nullptr ? A->next : headB;
B = B != nullptr ? B->next : headA;
}
return A;
}
};
走到尽头见不到你,于是走过你来时的路,等到相遇时才发现,你也走过我来时的路。——来自评论区
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
思路: 从前往后找偶数,从后往前找偶数,找到后交换。
代码:
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
int n = nums.size();
int l = 0;
int r = n - 1;
while(l < r) {
if(nums[l] % 2 != 0) {
l ++;
continue;
}
if(nums[r] % 2 == 0) {
r --;
continue;
}
//交换nums[l]和nums[r]
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
l ++;
r --;
}
return nums;
}
};
剑指 Offer 57. 和为s的两个数字
代码:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
int l = 0;
int r = n - 1;
while(l < r) {
if(nums[l] + nums[r] == target) {
return { nums[l], nums[r] };
}
if(nums[l] + nums[r] < target) {
l ++;
} else {
r --;
}
}
return {};
}
};
剑指 Offer 58 - I. 翻转单词顺序
class Solution {
public:
string reverseWords(string s) {
int n = s.length();
int i = 0;
int j = 0;
stack<string> stk;
while(i < n) {
if(s[i] == ' ') {
i ++;
continue;
}
j = i;
while(j < n && s[j] != ' ') {
j ++;
}
stk.push(s.substr(i,j-i));
// cout << s.substr(i,j-i) << endl;
i = j + 1;
}
string ans = "";
while(!stk.empty()) {
if(stk.size() == 1) {
ans += stk.top();
} else {
ans += stk.top() + " ";
}
stk.pop();
}
return ans;
}
};