Leetcode周赛 | 2023-7-30--我真是个废物

题1

体会

根本没想到用双指针。原因是，没想到还要用一个字典去维护子数组中各个数字的出现频次，以及出现频次不小于1 (也就是大于0) 的数字个数。

这里的双重循环也很巧妙，根本想不到。

class Solution:
    def countCompleteSubarrays(self, nums: List[int]) -> int:
        # 查看目标需要有多少个不同的数字
        m = len(set(nums))

        n = len(nums)
        l, r = 0, 0
        # 分别记录出现的频次和出现频次大于 0 的数的个数
        cnt = Counter()
        different_values = 0
        ans = 0
        while l < n:
            while r < n and different_values < m:
                cnt[nums[r]] += 1
                # 频次变为 1 时，出现频次大于 0 的数的个数增加 1
                if cnt[nums[r]] == 1: different_values += 1
                r += 1
            if different_values < m: break
            # [l, r-1], ..., [l, n-1] 总共有 n - r + 1 个区间
            ans += n - r + 1
            cnt[nums[l]] -= 1
            # 频次变为 0 时，出现频次大于 0 的数的个数减少 1
            if cnt[nums[l]] == 0: different_values -= 1
            l += 1
        return ans

上面的代码中，根本没用到 Counter() ， 就是当一个字典来用的。换成字典是一样的。

class Solution:
    def countCompleteSubarrays(self, nums: List[int]) -> int:
       # 查看目标需要有多少个不同的数字
        m = len(set(nums))

        n = len(nums)
        l, r = 0, 0
        # 分别记录出现的频次和出现频次大于 0 的数的个数
        cnt = {}
        different_values = 0
        ans = 0
        while l < n:
            while r < n and different_values < m:
                cnt[nums[r]] = cnt.get(nums[r],0)+1
                # 频次变为 1 时，出现频次大于 0 的数的个数增加 1
                if cnt[nums[r]] == 1: different_values += 1
                r += 1
            if different_values < m: break
            # [l, r-1], ..., [l, n-1] 总共有 n - r + 1 个区间
            ans += n - r + 1
            cnt[nums[l]] -= 1
            # 频次变为 0 时，出现频次大于 0 的数的个数减少 1
            if cnt[nums[l]] == 0: different_values -= 1
            l += 1
        return ans

我的代码

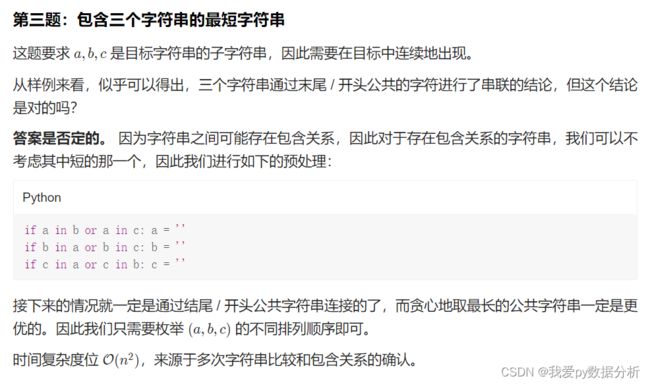
题2

体会

class Solution:
    def minimumString(self, a: str, b: str, c: str) -> str:
      
        length, res = inf, ''
        if a in b or a in c: a = ''
        if b in a or b in c: b = ''
        if c in a or c in b: c = ''
        
        for x, y, z in permutations((a, b, c)):
            
            tmp = ''
            for i in range(min(len(x), len(y)), 0, -1):
                if x[-i:] == y[:i]: tmp = x + y[i:]; break
            else: tmp = x + y
            
            for i in range(min(len(tmp), len(z)), 0, -1):
                if tmp[-i:] == z[:i]: tmp = tmp + z[i:]; break
            else: tmp = tmp + z
            
            if len(tmp) < length or (len(tmp) == length and tmp < res):
                length = len(tmp)
                res = tmp
            
        return res

太恐怖了，这个编程技巧， if else 还能这样用的 ？

本题只有三个字符串，一共可能的组合也没几种，那就全部遍历！一定要区分，是处理固定个数目标的题，还是处理N个目标的题，固定个数的可以全部遍历。

我的代码

题3

体会

数位DP我不配。

mod = 10 ** 9 + 7
class Solution:
    def countSteppingNumbers(self, low: str, high: str) -> int:
        low = str(int(low) - 1)
        @cache
        def getRes(idx, start, bind, lastVal):
            if idx == len(x): return 1 if start else 0
            
            # 如果数字还没开始，那么可以到下一个位再开始
            res = 0 if start else getRes(idx+1, False, False, 0)

            # 可能转移成的数字：如果数字还未开始
            for i in ([lastVal-1, lastVal+1] if start else range(1, 10)):
                # 判断数字是否合法：有无本身超出数字集 / 大于了给定的 x 的情况
                if i < 0 or i > 9: continue
                if bind and i > x[idx]: break
                # 看上界是否还有限制作用
                note = bind and i == x[idx]
                res += getRes(idx+1, True, note, i)
            
            return res % mod
        
        x = [int(x) for x in high]
        ans = getRes(0, False, True, 0)
        getRes.cache_clear()
        # 注意这里要清空下 cache，否则同个状态对于两个 x 判断结果不同会造成答案错误
        
        x = [int(x) for x in low]
        ans -= getRes(0, False, True, 0)
        getRes.cache_clear()

        return ans % mod # 减了之后可能变成负数，记得取模

我的代码