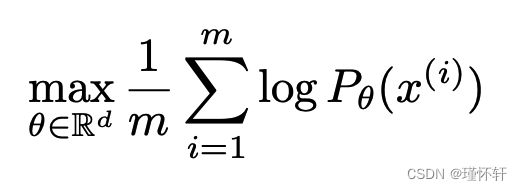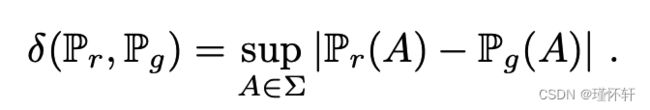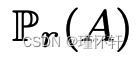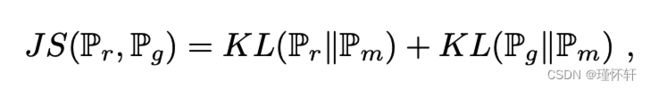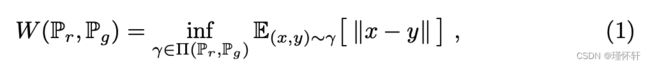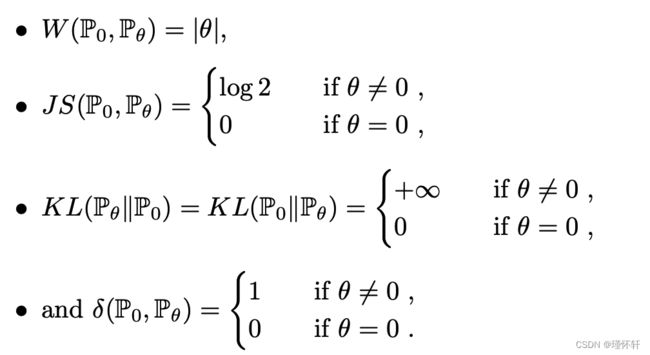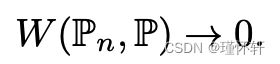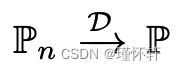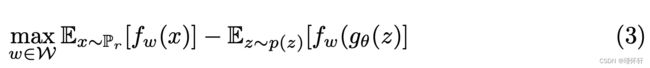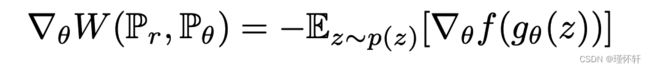【论文】【生成对抗网络五】Wasserstein GAN (WGAN)
【题目、作者】:
紫色:要解决的问题或发现的问题
红色:重点内容
棕色:关联知识,名称
绿色:了解内容,说明内容
论文地址: 论文下载
本篇文章仅为原文翻译,仅作参考。
一、导言
本文关注的问题是无监督学习。主要是,学习概率分布意味着什么?对此的经典答案是学习概率密度。这通常是通过定义密度![]() 的参数族并找到和我们数据最大相似性的族,即:如果我们有真实的数据示例
的参数族并找到和我们数据最大相似性的族,即:如果我们有真实的数据示例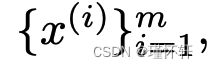 ,我们将解决这个问题:
,我们将解决这个问题:
如果实际数据分布  承认有密度,而
承认有密度,而 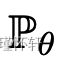 是参数化密度
是参数化密度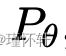 的分布,那么渐近地,这相当于最小化 Kullback-Leibler 散度 KL(
的分布,那么渐近地,这相当于最小化 Kullback-Leibler 散度 KL( ||
|| 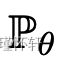 )。
)。
为了使这一点有意义,我们需要模型密度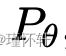 存在。在我们处理低维流形支持的分布的相当常见的情况下,情况并非如此。因此,模型流形和真实分布的支持不太可能具有不可忽略的交集(参见[1]),这意味着KL距离没有定义(或只是无限)。
存在。在我们处理低维流形支持的分布的相当常见的情况下,情况并非如此。因此,模型流形和真实分布的支持不太可能具有不可忽略的交集(参见[1]),这意味着KL距离没有定义(或只是无限)。
典型的补救措施是在模型分布中添加噪声项。这就是为什么经典机器学习文献中描述的几乎所有生成模型都包含噪声分量的原因。在最简单的情况下,假设高斯噪声具有相对较高的带宽,以涵盖所有示例。例如,众所周知,在图像生成模型的情况下,这种噪声会降低样本的质量并使它们变得模糊。例如,我们可以在最近的论文[23]中看到,当像素已经归一化为在[0,1]范围内时,当最大化似然时,添加到模型中的噪声的最佳标准差约为0.1。这是一个非常高的噪声量,以至于当论文报告其模型的样本时,他们不会添加报告似然数的噪声项。换句话说,添加的噪声项对于问题显然是不正确的,但需要使最大似然法起作用。
与其估计可能不存在的 密度,我们可以定义一个具有固定分布p(z)的随机变量Z,并将其传递到参数函数g(θ):Z→X(通常是某种神经网络),该函数直接按照某个分布
密度,我们可以定义一个具有固定分布p(z)的随机变量Z,并将其传递到参数函数g(θ):Z→X(通常是某种神经网络),该函数直接按照某个分布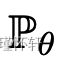 生成样本。通过改变 θ,我们可以改变这个分布并使其接近实际数据分布
生成样本。通过改变 θ,我们可以改变这个分布并使其接近实际数据分布  。这在两个方面很有用。首先,与密度不同,这种方法可以表示局限于低维流形的分布。其次,轻松生成样本的能力通常比知道密度的数值更有用(例如,在给定输入图像的情况下考虑输出图像的条件分布时的图像超分辨率或语义分割)。通常,在给定任意高维密度的情况下,生成样本在计算上是困难的[16]。
。这在两个方面很有用。首先,与密度不同,这种方法可以表示局限于低维流形的分布。其次,轻松生成样本的能力通常比知道密度的数值更有用(例如,在给定输入图像的情况下考虑输出图像的条件分布时的图像超分辨率或语义分割)。通常,在给定任意高维密度的情况下,生成样本在计算上是困难的[16]。
变分自动编码器(VAE)[9]和生成对抗网络(GAN)[4]是这种方法的众所周知的例子。由于VAE专注于示例的近似可能性,因此它们具有标准模型的局限性,需要摆弄其他噪声项。GAN在目标函数的定义方面提供了更大的灵活性,包括Jensen-Shannon[4],所有f发散[17]以及一些奇特的组合[6]。另一方面,训练 GAN 以微妙和不稳定而闻名,其原因在 [1] 中进行了理论研究。
在本文中,我们将注意力集中在测量模型分布和实际分布有多接近的各种方法上,或者等效地,在定义距离或散度ρ(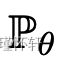 ,
, )的各种方法上。这些距离之间最根本的区别是它们对概率分布序列收敛的影响。分布
)的各种方法上。这些距离之间最根本的区别是它们对概率分布序列收敛的影响。分布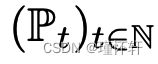 的一个序列收敛当且仅当存在分布 P∞使得 ρ(Pt , P∞ ) 趋于零,这取决于距离 ρ 的精确定义方式。非正式地说,非正式地,当距离 ρ 使分布序列更容易收敛时,它会诱导较弱的拓扑.1【更确切地说,当 ρ 下的收敛序列集是 ρ′ 下的收敛序列集时,ρ 诱导的拓扑比 ρ′ 诱导的拓扑弱。】 第 2 节阐明了流行的概率距离在这方面的差异。
的一个序列收敛当且仅当存在分布 P∞使得 ρ(Pt , P∞ ) 趋于零,这取决于距离 ρ 的精确定义方式。非正式地说,非正式地,当距离 ρ 使分布序列更容易收敛时,它会诱导较弱的拓扑.1【更确切地说,当 ρ 下的收敛序列集是 ρ′ 下的收敛序列集时,ρ 诱导的拓扑比 ρ′ 诱导的拓扑弱。】 第 2 节阐明了流行的概率距离在这方面的差异。
为了优化参数 θ,当然需要定义我们的模型分布 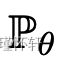 ,以使连续映射 θ→
,以使连续映射 θ→ 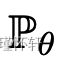 的方式进行定义。连续性意味着当一系列参数 θt 收敛到 θ 时,分布
的方式进行定义。连续性意味着当一系列参数 θt 收敛到 θ 时,分布 也会收敛到
也会收敛到 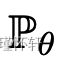 。但是,必须记住,分布
。但是,必须记住,分布  收敛的概念取决于我们计算分布之间距离的方式。这个距离越弱,就越容易定义从θ空间到
收敛的概念取决于我们计算分布之间距离的方式。这个距离越弱,就越容易定义从θ空间到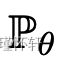 空间的连续映射,因为分布更容易收敛。如果 ρ 是我们两个分布之间距离的概念,我们希望有一个连续的损失函数 θ → ρ(
空间的连续映射,因为分布更容易收敛。如果 ρ 是我们两个分布之间距离的概念,我们希望有一个连续的损失函数 θ → ρ(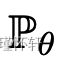 ,
, ),这相当于在使用分布之间距离 ρ 时有映射 θ →
),这相当于在使用分布之间距离 ρ 时有映射 θ → 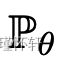 。
。
本文的贡献是:
- 在第 2 节中,我们对地球移动 (EM) 距离与学习分布上下文中使用的流行概率距离和散度相比的行为进行了全面的理论分析。
- 在第 3 节中,我们定义了一种称为 Wasserstein-GAN 的 GAN 形式,它最小化了 EM 距离的合理和有效的近似,并且我们从理论上证明了相应的优化问题是合理的。
- 在第 4 节中,我们凭经验表明 WGAN 解决了 GAN 的主要训练问题。特别是,训练WGAN不需要在训练鉴别器和生成器时保持谨慎的平衡,也不需要仔细设计网络架构。GAN中典型的模式丢弃现象也大大减少。WGAN最引人注目的实际好处之一是能够通过训练鉴别器达到最佳性来连续估计EM距离。绘制这些学习曲线不仅对调试和超参数搜索有用,而且与观察到的样本质量非常相关。
二、不同的距离
我们现在介绍我们的符号。设 X 是一个紧凑的度量集(例如图像的空间 ),让 Σ 表示 X 的所有 Borel 子集的集合。设 Prob(X) 表示在 X 上定义的概率测度空间。现在我们可以定义两个分布
),让 Σ 表示 X 的所有 Borel 子集的集合。设 Prob(X) 表示在 X 上定义的概率测度空间。现在我们可以定义两个分布  、
、  ∈ Prob(X) 之间的基本距离和发散:
∈ Prob(X) 之间的基本距离和发散:
- 总变化 (TV) 距离
- KL散度
其中  和
和  都假定是绝对连续的,因此相对于在 X 上定义的相同度量μ允许密度。2【回想一下,概率分布
都假定是绝对连续的,因此相对于在 X 上定义的相同度量μ允许密度。2【回想一下,概率分布  ∈ Prob(X) 允许密度 pr(x) 相对于μ,也就是说,
∈ Prob(X) 允许密度 pr(x) 相对于μ,也就是说,
∀A ∈ Σ,  =
=![]() ,当且仅它就μ而言是绝对连续的, 也就是说,
,当且仅它就μ而言是绝对连续的, 也就是说,
KL 散度是著名的不对称的,当存在 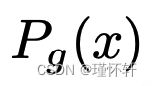 = 0 且
= 0 且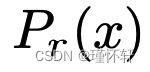 > 0 的点时可能是无限的。
> 0 的点时可能是无限的。
- JS散度
其中  是 (
是 ( +
+ )/2。这种散度是对称的,并且总这样定义的,因为我们可以选择μ =
)/2。这种散度是对称的,并且总这样定义的,因为我们可以选择μ =  。
。
- 推土机(EM)距离或 Wasserstein-1
其中 表示这些下降联合分布γ(x,y),联合分布的边缘分别是Pr和Pg.直观地,γ(x,y)表示必须从x到y传输多少“质量”才能将分布Pr转换为分布Pg。EM距离是最佳运输计划的“成本”。
表示这些下降联合分布γ(x,y),联合分布的边缘分别是Pr和Pg.直观地,γ(x,y)表示必须从x到y传输多少“质量”才能将分布Pr转换为分布Pg。EM距离是最佳运输计划的“成本”。
以下示例说明了看似简单的概率分布序列如何在 EM 距离下收敛,但在上面定义的其他距离和散度下不收敛。
示例 1(学习平行线)。
设 Z ∼ U [0, 1] 单位区间上的均匀分布。设 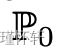 是 (0,Z) ∈
是 (0,Z) ∈  (x 轴上的 0 和 y 轴上的随机变量 Z)的分布,在穿过原点的垂直直线上均匀分布。现在设 gθ(z)= (θ,z) 与 θ 一个实参数。不难看出,在这种情况下,
(x 轴上的 0 和 y 轴上的随机变量 Z)的分布,在穿过原点的垂直直线上均匀分布。现在设 gθ(z)= (θ,z) 与 θ 一个实参数。不难看出,在这种情况下,
当θt→0时,序列 在EM距离下收敛到
在EM距离下收敛到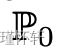 ,但在JS,KL,反向KL或TV发散下根本不收敛。图 1 说明了 EM 和 JS 距离的情况。
,但在JS,KL,反向KL或TV发散下根本不收敛。图 1 说明了 EM 和 JS 距离的情况。
 图 1:当 ρ 是 EM 距离(左图)或 JS 散度(右图)时,这些图显示 ρ(Pθ,P0) 是 θ 的函数。EM 图是连续的,并在任何地方提供可用的梯度。JS图不是连续的,并且不提供可用的梯度。
图 1:当 ρ 是 EM 距离(左图)或 JS 散度(右图)时,这些图显示 ρ(Pθ,P0) 是 θ 的函数。EM 图是连续的,并在任何地方提供可用的梯度。JS图不是连续的,并且不提供可用的梯度。
示例 1 为我们提供了一个案例,通过对 EM 距离进行梯度下降,我们可以学习低维流形上的概率分布。其他距离和发散无法做到这一点,因为由此产生的损失函数甚至不是连续的。
尽管这个简单示例具有不相交支座的分布,但当支座具有包含在一组测量值零中的非空交集时,同样的结论成立。当两个低维流形在一般位置相交时,恰好就是这种情况[1].
由于 Wasserstein 距离比 JS 距离弱得多【附录A中显示了为什么会发生这种情况的论点,以及我们如何得出Wasserstein是我们真正应该优化的想法。我们强烈鼓励不怕数学的有兴趣的读者验证它。】,我们现在可以问 ![]() 在温和假设下是否是 θ 上的连续损失函数。正如我们现在所陈述和证明的那样,这一点以及更多是真实的。
在温和假设下是否是 θ 上的连续损失函数。正如我们现在所陈述和证明的那样,这一点以及更多是真实的。
定理 1.
设 ![]() 是 X 上的固定分布。设 Z 是另一个空间
是 X 上的固定分布。设 Z 是另一个空间![]() 上的随机变量(例如高斯变量)。设 g :
上的随机变量(例如高斯变量)。设 g :![]() ×
×  → X 是一个函数,表示为 gθ(z),z 是第一个坐标,θ 是第二个坐标。设
→ X 是一个函数,表示为 gθ(z),z 是第一个坐标,θ 是第二个坐标。设 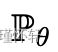 表示 gθ(Z) 的分布。然后
表示 gθ(Z) 的分布。然后
- 如果 g 在 θ 中是连续的,则
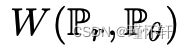 也是连续的。
也是连续的。 - 如果 g 是局部 Lipschitz 并且满足正则性假设 1,则
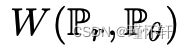 到处都是连续的,几乎到处都是可微分的。
到处都是连续的,几乎到处都是可微分的。 - 对于詹森-香农散度
 和所有 KL,语句 1-2 是错误的。
和所有 KL,语句 1-2 是错误的。
证明。见附录C
以下推论告诉我们,通过最小化EM距离来学习神经网络是有意义的(至少在理论上)。
推论 1.
设 gθ 是任何由 θ 参数化的前馈神经网络 【前馈神经网络是指由仿射变换和逐点非线性组成的函数,它们是平滑的 Lipschitz 函数(例如 sigmoid、tanh、elu、softplus 等)。注意:该声明也适用于整流器非线性,但证明更具技术性(即使非常相似),因此我们省略了它。】,并且 p(z) 是 z 上的先验,使得  (例如高斯、均匀等)。
(例如高斯、均匀等)。
然后满足假设 1,因此 ![]() 在任何地方都是连续的,几乎在任何地方都是可微的。
在任何地方都是连续的,几乎在任何地方都是可微的。
证明。见附录C
所有这些都表明,对于我们的问题来说,EM是一个比至少Jensen-Shannon散度更合理的成本函数。以下定理描述了由这些距离和发散引起的拓扑的相对强度,KL最强,其次是JS和TV,EM最弱。
定理 2.
设 ![]() 是紧密空间 X 上的分布,
是紧密空间 X 上的分布,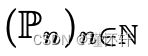 是 X 上的分布序列。然后,将所有极限视为 n → ∞,
是 X 上的分布序列。然后,将所有极限视为 n → ∞,
1. 以下语句是等效的
2. 以下语句是等效的
3. 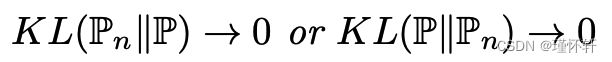 ,(1) 有暗示了。{不考虑对称性,其实就是JS散度那一条}
,(1) 有暗示了。{不考虑对称性,其实就是JS散度那一条}
4.(1) 中的语句表示 (2) 中的语句。
证明。见附录C
这突出了这样一个事实,即在学习低维流形支持的分布时,KL、JS 和 TV 距离不是合理的成本函数。但是,在该设置中,EM距离是合理的。这显然将我们引到下一节,我们将介绍优化EM距离的实用近似值。
三、Wasserstein GAN
同样,定理2指出了这样一个事实,即![]() 在优化时可能比
在优化时可能比 具有更好的性质。然而,(1)中的下确界非常棘手。另一方面,康托罗维奇-鲁宾斯坦对偶性[22]告诉我们:
具有更好的性质。然而,(1)中的下确界非常棘手。另一方面,康托罗维奇-鲁宾斯坦对偶性[22]告诉我们:
其中上确界在所有 1-L函数上 : 请注意,如果我们用
请注意,如果我们用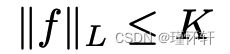 替换
替换  考虑 K-Lipschitz 对于某个常数 K),那么我们最终得到
考虑 K-Lipschitz 对于某个常数 K),那么我们最终得到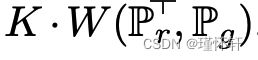 。因此,如果我们有一个参数化族函数
。因此,如果我们有一个参数化族函数 对于某些 K 来说都是 K-Lipschitz,我们可以考虑解决问题
对于某些 K 来说都是 K-Lipschitz,我们可以考虑解决问题
如果(2)中的上确界达到一些 (一个非常强大的假设,类似于证明判别器的一致性时假设),这个过程将产生
(一个非常强大的假设,类似于证明判别器的一致性时假设),这个过程将产生![]() 的计算,直到乘法常数。此外,我们可以考虑通过估计
的计算,直到乘法常数。此外,我们可以考虑通过估计 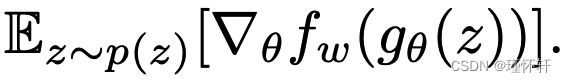 通过方程 (2) 反向传播来微分
通过方程 (2) 反向传播来微分 ![]() (同样,直到一个常数)。虽然这都是直觉,但我们现在证明这个过程是在最优假设下的原则。
(同样,直到一个常数)。虽然这都是直觉,但我们现在证明这个过程是在最优假设下的原则。
定理 3.
让 成为任何分布。设
成为任何分布。设 是 gθ(Z) 的分布,其中 Z 是密度为 p 的随机变量,gθ 是满足假设 1 的函数。然后,有一个解决方案
是 gθ(Z) 的分布,其中 Z 是密度为 p 的随机变量,gθ 是满足假设 1 的函数。然后,有一个解决方案 的问题:
的问题:
当两个术语都明确定义时。
证明。见附录C
现在来了找到求解方程(2)中最大化问题的函数f的问题。为了大致近似这一点,我们可以做的是训练一个参数化的神经网络,其权重w位于紧凑空间 中,然后通过
中,然后通过 反向传播,就像我们对典型GAN所做的那样。请注意,
反向传播,就像我们对典型GAN所做的那样。请注意, 是紧密的事实意味着对于仅依赖于
是紧密的事实意味着对于仅依赖于 而不是单个权重的某些 K,所有函数 fw 都将是 K-Lipschitz,因此近似 (2) 到不相关的比例因子和“惩罚项” fw 的容量。为了使参数w位于紧凑的空间中,我们可以做的简单事情是在每次梯度更新后将权重夹在一个固定的空间上(例如
而不是单个权重的某些 K,所有函数 fw 都将是 K-Lipschitz,因此近似 (2) 到不相关的比例因子和“惩罚项” fw 的容量。为了使参数w位于紧凑的空间中,我们可以做的简单事情是在每次梯度更新后将权重夹在一个固定的空间上(例如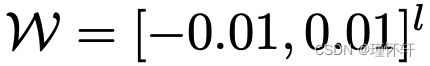 )。Wasserstein 生成对抗网络(WGAN)过程在算法1中描述。
)。Wasserstein 生成对抗网络(WGAN)过程在算法1中描述。
权重裁剪显然是强制执行 Lipschitz 约束的一种糟糕方法。如果裁剪参数很大,则任何权重都可能需要很长时间才能达到其极限,从而使训练惩罚项达到最佳变得更加困难。如果裁剪很小,则当层数很大或不使用批量归一化(例如在 RNN 中)时,这很容易导致梯度消失。我们尝试了简单的变体(例如将权重投影到球体上),几乎没有差异,并且由于其简单性和已经很好的性能,我们坚持使用权重裁剪。但是,我们确实将神经网络环境中强制执行Lipschitz约束的主题留给了进一步的研究,并且我们积极鼓励感兴趣的研究人员改进这种方法。
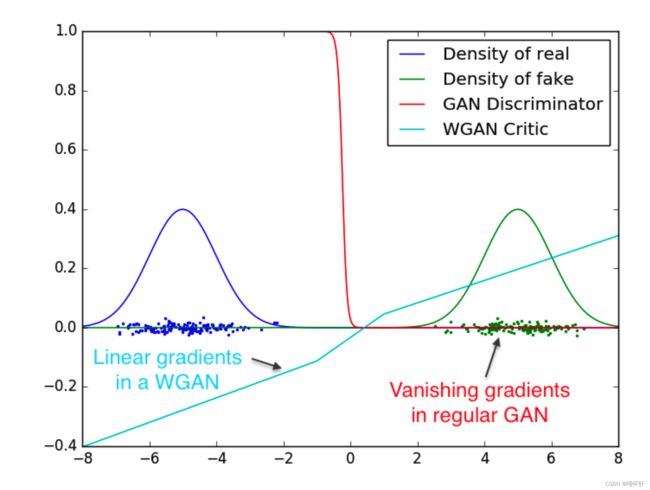
事实上,EM 距离是连续且可微的 a.e.意思是我们可以(并且应该)训练惩罚项直到最优。论点很简单,我们训练惩罚项越多,我们得到的 Wasserstein 梯度就越可靠,这实际上是有用的,因为 Wasserstein 几乎在任何地方都是可微的。对于 JS,随着判别器变得更好,梯度变得更可靠,但真实梯度为 0,因为 JS 局部饱和,我们得到消失梯度,如本文的图 1 和 [1] 的定理 2.4 所示。在图 2 中,我们展示了这一概念的证明,其中我们训练 GAN 判别器和 WGAN 惩罚项直至最优。鉴别器很快就能学会区分假货和真货,并且正如预期的那样,没有提供可靠的梯度信息。然而,惩罚项不能饱和,并且会收敛到一个线性函数,该函数在各处都给出非常干净的梯度。我们限制权重的事实限制了函数在空间的不同部分最多呈线性增长,迫使最优惩罚项具有这种行为。
也许更重要的是,我们可以训练惩罚项直到最佳,这使得当我们这样做时不可能模式崩溃。这是因为模式崩溃来自这样一个事实,即固定鉴别器的最佳生成器是鉴别器分配最高值的点上的增量总和,如 [4] 观察到并在 [11] 中突出显示。
在下一节中,我们将展示我们新算法的实际好处,并对其行为与传统▁GAN▁的行为进行深入比较。
图 2:学习区分两个高斯时的最佳鉴别器和惩罚器。正如我们所看到的,最小最大GAN的判别器饱和并导致梯度消失。我们的WGAN评论家在空间的所有部分都提供了非常干净的渐变。
四、 实证结果
我们使用我们的▁Wasserstein-GAN▁算法进行了图像生成实验,并表明与标准▁GAN▁中使用的公式相比,使用该算法具有显著的实际优势。
我们声称有两个主要好处:
- 与发生器的收敛性和样本质量相关的有意义的损失指标
- 改进优化过程的稳定性
4.1 实验程序
我们对图像生成进行实验。要学习的目标分布是LSUN-Rooms数据集[24] - 室内卧室的自然图像集合。我们的基线比较是DCGAN [18],这是一种具有卷积架构的GAN,使用标准GAN程序使用−log D技巧[4]进行训练。生成的样本是大小为 64x64 像素的 3 通道图像。我们使用算法 1 中指定的超参数进行所有实验。
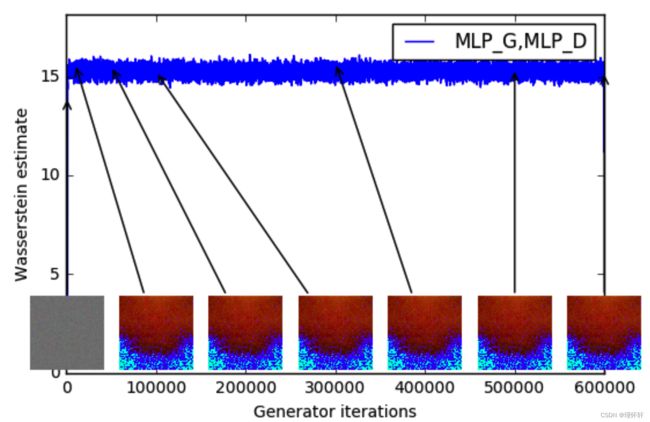
图 3:不同训练阶段的训练曲线和样本。我们可以看到较低的误差和更好的样品质量之间存在明显的相关性。左上:生成器是一个 MLP,有 4 个隐藏层,每层有 512 个单元。随着训练的进行和样本质量的提高,损失会持续减少。右上:生成器是标准的DCGAN。损失迅速减少,样品质量也随之提高。在上面的两个图中,惩罚器都是没有 sigmoid 的 DCGAN,因此损失可以进行比较。下半部分:生成器和鉴别器都是具有相当高学习率的 MLP(因此训练失败)。损失是恒定的,样品也是恒定的。训练曲线通过中值滤波器进行可视化。
4.2 有意义的损失度量
由于 WGAN 算法试图在每次生成器更新之前相对较好地训练惩罚器 f(算法 1 中的第 2-8 行)(算法 1 中的第 10 行),因此此时的损失函数是 EM 距离的估计值,直至与我们约束 f 的 Lipschitz 常数的方式相关的常数因子。
我们的第一个实验说明了这种估计如何与生成样本的质量密切相关。除了卷积DCGAN架构外,我们还进行了实验,将生成器或生成器和注释器替换为具有512个隐藏单元的4层ReLU-MLP。
据我们所知,这是GAN文献中第一次显示这样的属性,其中GAN的损失显示了收敛的性质。在对抗网络中进行研究时,此属性非常有用,因为不需要盯着生成的样本来找出故障模式并获得有关哪些模型比其他模型做得更好的信息。
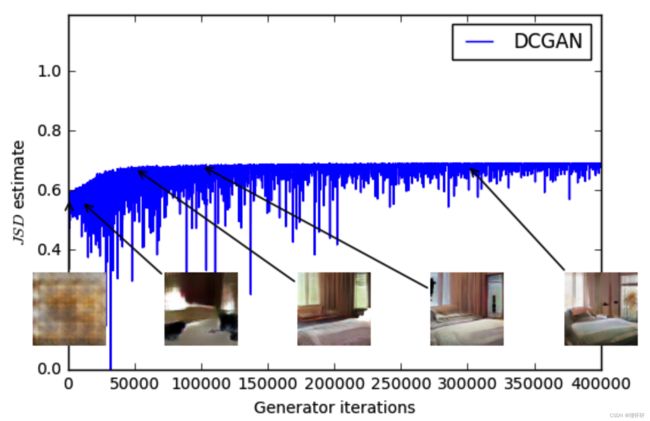
图 4:使用 GAN 程序训练的 MLP 生成器(左上)和 DCGAN 生成器(右上)的 JS 估计值。两者都有一个DCGAN鉴别器。两条曲线的误差都在增加。DCGAN的样本变得更好,但JS估计值增加或保持不变,表明样本质量和损失之间没有显着相关性。底部:带有生成器和鉴别器的MLP。无论样品质量如何,曲线都会上下波动。所有训练曲线均通过与图3相同的中值滤波器。
然而,我们并没有声称这是一种定量评估生成模型的新方法。取决于惩罚器架构的恒定缩放因子意味着很难将模型与不同的惩罚器进行比较。更重要的是,在实践中,惩罚器没有无限的能力这一事实使得很难知道我们的估计与EM距离到底有多近。话虽如此,我们已经成功地使用损失指标来反复验证我们的实验,并且没有失败,我们认为这是训练GAN的巨大改进,而以前没有这种工具。
相比之下,图4绘制了GAN训练期间JS距离的GAN估计值的演变。更准确地说,在GAN训练期间,鉴别器被训练为最大化 。
这个数量显然与样本质量相关性较差。另请注意,JS 估计通常保持不变或上升而不是下降。事实上,它通常非常接近 log 2 ≈ 0.69,这是 JS 距离所取的最高值。换句话说,JS 距离饱和,鉴别器具有零损失,并且生成的样本在某些情况下是有意义的(DCGAN 生成器,右上图),而在其他情况下则崩溃为单个无意义的图像 [4]。最后一个现象已在 [1] 中得到了理论上的解释,并在 [11] 中得到了强调。
当使用−log D技巧[4]时,鉴别器损耗和生成器损耗是不同的。附录E中的图8报告了GAN训练的相同图,但使用生成器损耗而不是鉴别器损耗。这不会改变结论。
最后,作为一个负面结果,我们报告说,当在惩罚器上使用基于动量的优化器(如 Adam [8](β1 > 0))或使用高学习率时,WGAN 训练有时会变得不稳定。由于惩罚器的损失是非平稳的,基于动量的方法似乎表现更差。我们认为动量是一个潜在的原因,因为随着损失的增加和样本的恶化,Adam 步长和梯度之间的余弦通常会变成负值。该余弦唯一为负值的地方是在这些不稳定的情况下。因此,我们改用 RMSProp [21],即使在非常不稳定的问题上也能表现良好 [13]。
4.3 提高稳定性
WGAN的好处之一是它允许我们训练惩罚器直到最佳状态。当惩罚器被训练完成时,它只是给生成器一个损失,我们可以像任何其他神经网络一样训练它。这告诉我们,我们不再需要正确平衡生成器和鉴别器的容量。惩罚器越好,我们用来训练生成器的梯度质量就越高。
我们观察到,当改变生成器的架构选择时,WGAN比GAN更健壮。我们通过在三种生成器架构上运行实验来说明这一点:(1)卷积DCGAN生成器,(2)没有批量归一化且具有恒定数量的过滤器的卷积DCGAN生成器,以及(3)具有512个隐藏单元的4层ReLU-MLP。众所周知,最后两个在 GAN 中表现非常差。我们为WGAN惩罚器或GAN鉴别器保留卷积DCGAN架构。
图 5、6 和 7 显示了使用 WGAN 和 GAN 算法为这三种架构生成的示例。我们请读者参阅附录F以获取生成样品的完整页面。样品不是精心挑选的。
在实验中,我们没有看到WGAN算法模式崩溃的证据。
图 5:使用 DCGAN 生成器训练的算法。左:WGAN算法。右:标准GAN配方。两种算法都会生成高质量的样本。
图6:使用生成器训练的算法,没有批归一化和每层恒定数量的过滤器(而不是像[18]中那样每次都重复过滤器)。除了取消批归一化外,参数数量因此减少了一个数量级以上。左:WGAN算法。右:标准GAN公式。正如我们所看到的,标准GAN未能学习,而WGAN仍然能够生成样本。
图 7:使用 MLP 发生器训练的算法,具有 4 层和 512 个具有 ReLU 非线性的单元。参数数量与DCGAN相似,但缺乏用于图像生成的强归纳偏置。左:WGAN算法。右:标准GAN配方。WGAN方法仍然能够产生质量低于DCGAN的样品,并且比标准GAN的MLP质量更高。请注意 GAN MLP 中的模式崩溃程度很高。
五、相关工作
有许多关于所谓的积分概率指标(IPM)的工作[15]。给定 一组从
一组从 ![]() 到
到  的函数,我们可以定义
的函数,我们可以定义 
作为与函数类 相关的积分概率度量,很容易验证,如果对于每个
相关的积分概率度量,很容易验证,如果对于每个 我们有
我们有 (例如我们将考虑的所有示例),则
(例如我们将考虑的所有示例),则 是非负的,满足三角不等式,并且是对称的。因此,
是非负的,满足三角不等式,并且是对称的。因此, 是
是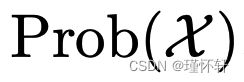 上的伪度量。
上的伪度量。
虽然 IPM 似乎共享类似的公式,但正如我们将看到不同类别的函数可以对完全不同的指标提出抗议。
- 通过KR[22],我们知道,当 F 是 1-Lipschitz 函数的集合时,
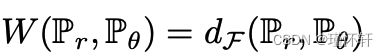 。此外,如果
。此外,如果  是 KL函数的集合,我们得到
是 KL函数的集合,我们得到  。
。 - 当
 是 -1 和 1 之间的所有可测量函数(或 -1 和 1 之间的所有连续函数)的集合时,我们检索
是 -1 和 1 之间的所有可测量函数(或 -1 和 1 之间的所有连续函数)的集合时,我们检索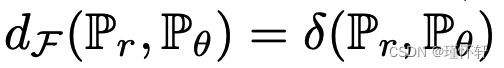 的总变化距离 [15]。这已经告诉我们,从 1-Lipschitz 到 1-有界函数会极大地改变空间的拓扑结构,以及
的总变化距离 [15]。这已经告诉我们,从 1-Lipschitz 到 1-有界函数会极大地改变空间的拓扑结构,以及 作为损失函数的规律性(如定理 1 和 2)。
作为损失函数的规律性(如定理 1 和 2)。 - 基于能量的GANs(EBGANs)[25]可以被认为是总变异距离的生成应用。这种联系在附录D中有深入的陈述和证明。连接的核心是鉴别器将扮演f最大化方程(4)的角色,而它唯一的限制是对于某个常数m在0和m之间。这将导致与限制在 −1 和 1 之间到与优化无关的恒定缩放因子相同的行为。因此,当判别器接近最优时,生成器的成本将接近总变化距离
 。
。
由于总变异距离显示出与JS相同的规律性,因此可以看出,EBGAN将遭受与经典GAN相同的问题,即无法训练鉴别器直到最优,从而将自己限制在非常不完美的梯度上。
- 最大平均差异 (MMD) [5] 是当
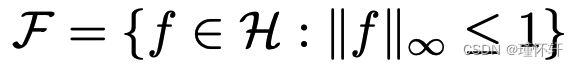 对于
对于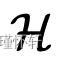 与给定核 k 关联的某个再现核希尔伯特空间 (RKHS) 时积分概率度量的特定情况:
与给定核 k 关联的某个再现核希尔伯特空间 (RKHS) 时积分概率度量的特定情况: 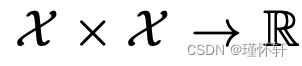 。正如[5]中所证明的,我们知道当内核是通用的时,MMD 是一个适当的度量,而不仅仅是一个伪度量。在
。正如[5]中所证明的,我们知道当内核是通用的时,MMD 是一个适当的度量,而不仅仅是一个伪度量。在  的特定情况下,m 是
的特定情况下,m 是  上的归一化勒贝格度量,我们知道
上的归一化勒贝格度量,我们知道 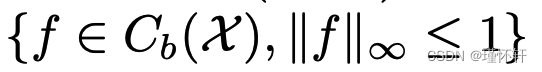 将包含在
将包含在  中,因此
中,因此 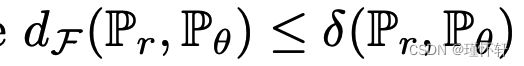 因此,MMD 距离作为损失函数的规律性至少与总变化的规律性一样差。然而,这是一个非常极端的情况,因为我们需要一个非常强大的内核来近似整个
因此,MMD 距离作为损失函数的规律性至少与总变化的规律性一样差。然而,这是一个非常极端的情况,因为我们需要一个非常强大的内核来近似整个 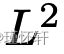 。然而,正如最近[20]所证明的那样,即使是高斯核也能够检测微小的噪声模式。这表明,特别是对于低带宽内核,距离可能接近饱和状态,类似于总变分或 JS。显然,不需要每个内核都是如此,并且弄清楚不同的 MMD 如何以及哪些更接近 Wasserstein 或总变异距离是一个有趣的研究主题。
。然而,正如最近[20]所证明的那样,即使是高斯核也能够检测微小的噪声模式。这表明,特别是对于低带宽内核,距离可能接近饱和状态,类似于总变分或 JS。显然,不需要每个内核都是如此,并且弄清楚不同的 MMD 如何以及哪些更接近 Wasserstein 或总变异距离是一个有趣的研究主题。
MMD的重要方面是,通过内核技巧,无需训练单独的网络来最大化RKHS球的方程(4)。然而,这样做的缺点是,评估MMD距离的计算成本随着用于估计(4)中期望的样本量呈二次增长。最后一点使得MMD具有有限的可扩展性,并且有时不适用于许多现实生活中的应用程序。MMD [5] 的线性计算成本估计在很多情况下使 MMD 非常有用,但它们的样本复杂性也较差。
- 生成时刻匹配网络(GMMNs)[10,2]是MMD的通用对应物。通过反向传播方程(4)的内核化公式,他们直接优化了
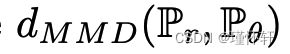 (当F与上一项相同时,IPM)。如前所述,这样做的优点是不需要单独的网络来近似最大化方程(4)。然而,GMMN的适用性有限。它们不成功的部分解释是二次成本与低带宽内核的样本数量和消失的分数的函数关系。此外,实践中使用的某些内核可能不适合在高维样本空间(如自然图像)中捕获非常复杂的距离。[19]表明,为了使典型的高斯MMD检验是可靠的(因为它的功效作为接近1的统计检验),我们需要样本的数量随着维度的数量线性增长。由于MMD计算成本随着用于估计方程(4)的批次中的样本数量而二次增长,这使得拥有可靠估计器的成本随维度数二次增长,这使得它非常不适用于高维问题。事实上,对于像 64x64 图像这样标准的东西,我们需要大小至少为 4096 的小批量(不考虑 [19] 范围内的常量,这将使这个数字大大增加)和每次迭代的总成本为 40962,当使用标准批量大小 64 时,比 GAN 迭代高出 5 个数量级以上。
(当F与上一项相同时,IPM)。如前所述,这样做的优点是不需要单独的网络来近似最大化方程(4)。然而,GMMN的适用性有限。它们不成功的部分解释是二次成本与低带宽内核的样本数量和消失的分数的函数关系。此外,实践中使用的某些内核可能不适合在高维样本空间(如自然图像)中捕获非常复杂的距离。[19]表明,为了使典型的高斯MMD检验是可靠的(因为它的功效作为接近1的统计检验),我们需要样本的数量随着维度的数量线性增长。由于MMD计算成本随着用于估计方程(4)的批次中的样本数量而二次增长,这使得拥有可靠估计器的成本随维度数二次增长,这使得它非常不适用于高维问题。事实上,对于像 64x64 图像这样标准的东西,我们需要大小至少为 4096 的小批量(不考虑 [19] 范围内的常量,这将使这个数字大大增加)和每次迭代的总成本为 40962,当使用标准批量大小 64 时,比 GAN 迭代高出 5 个数量级以上。
话虽如此,这些数字对MMD来说可能有点不公平,因为我们正在比较GAN的经验样本复杂性与MMD的理论样本复杂性,后者往往更糟。然而,在最初的GMMN论文[10]中,他们确实使用了大小为1000的小批量,比标准的32或64大得多(即使这会产生二次计算成本)。虽然存在线性计算成本作为样本数量函数的估计[5],但它们的样本复杂性更差,据我们所知,它们尚未应用于GMMN等生成上下文。
在另一项伟大的研究中,[14]最近的工作探索了Wasserstein距离在离散空间的限制玻尔兹曼机学习的背景下的使用。乍一看,动机似乎完全不同,因为流形设置仅限于连续空间,而在有限离散空间中,弱拓扑和强拓扑(分别为 W 和 JS 的拓扑)重合。然而,归根结底,关于我们的动机,更多的是没有。我们都希望以一种利用底层空间几何形状的方式比较分布,而 Wasserstein 允许我们做到这一点。
最后,[3]的工作展示了计算不同分布之间的Wasserstein差异的新算法。我们认为这个方向非常重要,也许可以带来评估生成模型的新方法。
六、结论
我们引入了一种我们认为是WGAN的算法,这是传统GAN训练的替代方案。在这个新模型中,我们展示了我们可以提高学习的稳定性,摆脱模式崩溃等问题,并提供有意义的学习曲线,对调试和超参数搜索有用。此外,我们证明了相应的优化问题是合理的,并提供了扩展的理论工作,突出了与分布之间其他距离的深层联系。
七、参考文献
-
[1] Martin Arjovsky and L ́eon Bottou. Towards principled methods for training generative adversarial networks. In International Conference on Learning Rep- resentations, 2017. Under review.
-
[2] Gintare Karolina Dziugaite, Daniel M. Roy, and Zoubin Ghahramani. Train- ing generative neural networks via maximum mean discrepancy optimization. CoRR, abs/1505.03906, 2015.
-
[3] Aude Genevay, Marco Cuturi, Gabriel Peyr ́e, and Francis Bach. Stochastic op- timization for large-scale optimal transport. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29, pages 3440–3448. Curran Associates, Inc., 2016.
-
[4] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde- Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adver- sarial nets. In Advances in Neural Information Processing Systems 27, pages 2672–2680. Curran Associates, Inc., 2014.
-
[5] Arthur Gretton, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Sch ̈olkopf, and Alexander Smola. A kernel two-sample test. J. Mach. Learn. Res., 13:723– 773, 2012.
-
[6] Ferenc Huszar. How (not) to train your generative model: Scheduled sampling, likelihood, adversary? CoRR, abs/1511.05101, 2015.
-
[7] Shizuo Kakutani. Concrete representation of abstract (m)-spaces (a characteri- zation of the space of continuous functions). Annals of Mathematics, 42(4):994– 1024, 1941.
-
[8] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimiza- tion. CoRR, abs/1412.6980, 2014.
-
[9] Diederik P. Kingma and Max Welling. Auto-encoding variational bayes. CoRR, abs/1312.6114, 2013.
-
[10] Yujia Li, Kevin Swersky, and Rich Zemel. Generative moment matching net- works. In Proceedings of the 32nd International Conference on Machine Learn- ing (ICML-15), pages 1718–1727. JMLR Workshop and Conference Proceed- ings, 2015.
-
[11] Luke Metz, Ben Poole, David Pfau, and Jascha Sohl-Dickstein. Unrolled gen- erative adversarial networks. Corr, abs/1611.02163, 2016.
-
[12] Paul Milgrom and Ilya Segal. Envelope theorems for arbitrary choice sets. Econometrica, 70(2):583–601, 2002.
-
[13] Volodymyr Mnih, Adri`a Puigdom`enech Badia, Mehdi Mirza, Alex Graves, Tim- othy P. Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asyn- chronous methods for deep reinforcement learning. In Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York City, NY, USA, June 19-24, 2016, pages 1928–1937, 2016.
-
[14] Gr ́egoire Montavon, Klaus-Robert Mu ̈ller, and Marco Cuturi. Wasserstein training of restricted boltzmann machines. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29, pages 3718–3726. Curran Associates, Inc., 2016.
-
[15] Alfred Mu ̈ller. Integral probability metrics and their generating classes of func- tions. Advances in Applied Probability, 29(2):429–443, 1997.
-
[16] Radford M. Neal. Annealed importance sampling. Statistics and Computing, 11(2):125–139, April 2001.
-
[17] Sebastian Nowozin, Botond Cseke, and Ryota Tomioka. f-gan: Training genera- tive neural samplers using variational divergence minimization. pages 271–279, 2016.
-
[18] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representa- tion learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015.
-
[19] Aaditya Ramdas, Sashank J. Reddi, Barnabas Poczos, Aarti Singh, and Larry Wasserman. On the high-dimensional power of linear-time kernel two-sample testing under mean-difference alternatives. Corr, abs/1411.6314, 2014.
-
[20] Dougal J Sutherland, Hsiao-Yu Tung, Heiko Strathmann, Soumyajit De, Aa- ditya Ramdas, Alex Smola, and Arthur Gretton. Generative models and model criticism via optimized maximum mean discrepancy. In International Confer- ence on Learning Representations, 2017. Under review.
-
[21] T. Tieleman and G. Hinton. Lecture 6.5—RmsProp: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning, 2012.
-
[22] C ́edric Villani. Optimal Transport: Old and New. Grundlehren der mathema- tischen Wissenschaften. Springer, Berlin, 2009.
-
[23] Yuhuai Wu, Yuri Burda, Ruslan Salakhutdinov, and Roger B. Grosse. On the quantitative analysis of decoder-based generative models. CoRR, abs/1611.04273, 2016.
-
[24] Fisher Yu, Yinda Zhang, Shuran Song, Ari Seff, and Jianxiong Xiao. LSUN: Construction of a large-scale image dataset using deep learning with humans in the loop. Corr, abs/1506.03365, 2015.
-
[25] Junbo Zhao, Michael Mathieu, and Yann LeCun. Energy-based generative adversarial network. Corr, abs/1609.03126, 2016.
【证明和附录请见原文】