Scratch 详解 流畅光线追踪(盲区)引擎：角度 + 一次函数 + 区域判断

【提示1】本文将全程使用原版积木实现这一功能，请不要在评论区发送扩展中有相应积木。若喜欢使用扩展，可以自行将本文介绍的方法用扩展积木替代。

【提示2】本文中代码里出现的所有最后带*号的变量，均为私有变量！

---

正文

        近日，我看见有些大佬的“光线追踪”类作品。这些个作品都是通过向周围的空间扫描墙壁，来确定盲点与可视点的边界。这意味着，程序的运行效率不会很高。并且，这种方法必须有实际的屏幕渲染才能使用，当一些使用情境不再依靠屏幕渲染时，这种方法就不能使用了。

        这个时候，我们就需要角度+函数+区域判断来完成这一目标。

        在接下来的文章中，我将会介绍两种使用场景下的不同程序效果的编写方式，其区别在于一种是区域判断，另一种是阴影覆盖；但两种方法都有相同的核心：用角度、一次函数进行区域划分。

---

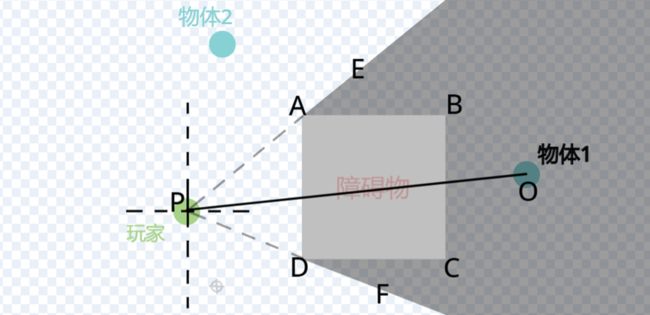
目标效果图（无需任何线条，图中加上线条是为了让程序更加可观）

【先行概述】本运行效果需积木数量约300。运行原理为：通过玩家与墙角的位置，计算出划分“盲区”与“ 可视区 ”的角度界线；再由地图中的物体自行判断是否在盲区中：是则隐藏，否则显示。

【优点】没有任何屏幕渲染，全盲算，运用于隐式盲区的场景（如联机枪战的小地图）。【缺点】整个物体会以一个中心点判断是否隐藏；物体越多运行越卡。

---

步骤1 | 理清思路

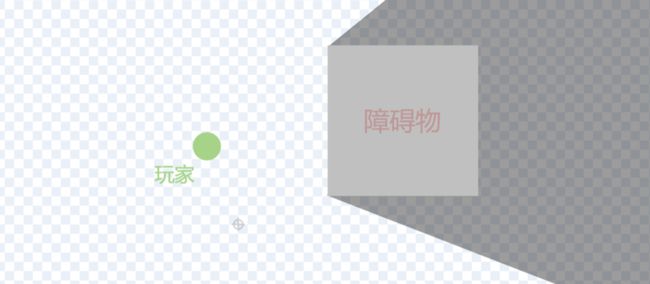
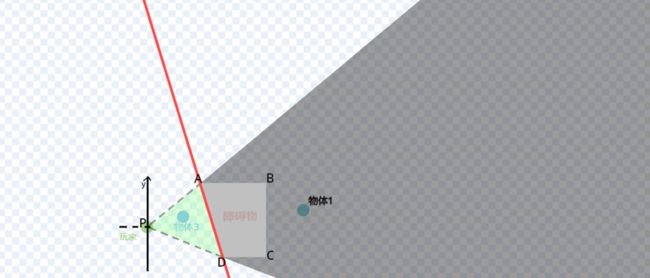
        简单以一个正方形作为一个障碍物，这个障碍物会遮挡玩家的视线（如下图阴影部分）。

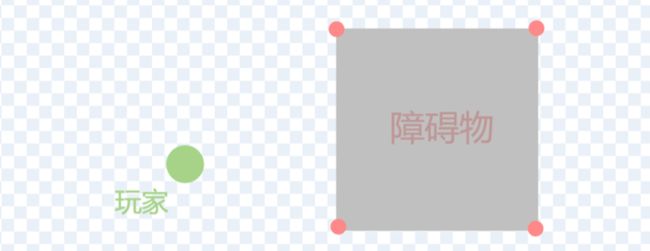
        那这个阴影部分，也就是盲区，和玩家的位置有什么联系呢？可以看见，这个障碍物有四个“墙角”（下图中标红点位置）：

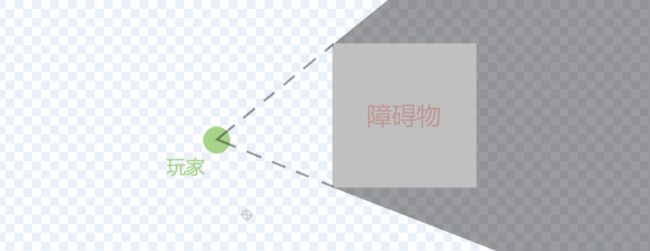
        不妨将玩家与墙角连接起来，我们发现：连接的线，恰好和“划分盲区与可视区的线”重合了。如下图：

        这下就好办了。“划分盲区与可视区的线”可以被很轻松地确定下来了！我们在图中标上几个点吧：

        不难发现规律：图中可以看见，物体1位于锐角∠EPF内部，是被遮挡的；而物体2位于锐角∠EPF外部，没有被遮挡。

那要如何判断是否位于角的内部呢？

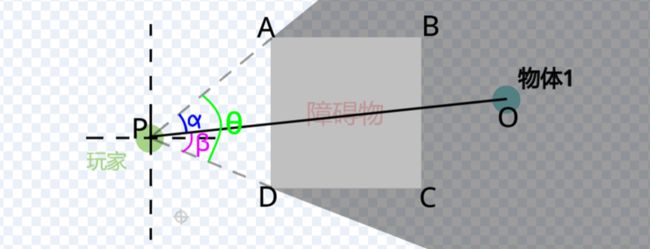
        如下图，连接物体和玩家，即连PO。PO将∠APD分成了两个部分：∠APO和∠DPO。

        将∠APD记为θ，∠APO记为α，∠DPO记为β。当物体被遮挡，即在∠APD内部的时候，α+β=θ。

        仍然将∠APD记为θ，∠APO记为α，∠DPO记为β。如下图，当物体未被遮挡，即在∠APD外部的时候，α+β≠θ。

        这样一来，我们便有了判断物体是否被遮挡的方法。

---

步骤2 | 计算角度，判断物体是否可见

*提示：下文出现的“缓存列表”相关名称，是本人的代码习惯。缓存列表主要用于：存储临时变量、存储计算参数、自定义积木返回值 等功能。

如何计算α、β、θ？

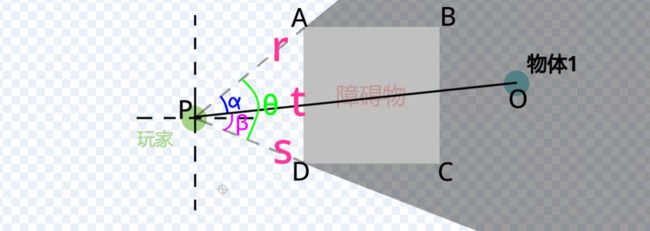
        已知玩家位置、墙角位置、物体位置，我们就可以分别计算出：玩家面向[墙角]的角度r、玩家面向[逆时针相邻的墙角]的角度s、玩家面向[物体]的角度t。（角度r、s、t即Scratch的方向）

        在上方的图中，可以看到：α=|t-r|、β=|s-t|、θ=|s-r|。

        玩家面向[墙角]的角度r、玩家面向[逆时针相邻的墙角]的角度s、玩家面向[物体]的角度t，都可以用下面这个积木算出来——[由 x1 y1 面向 x2 y2 的方向]：

        可以用反三角函数——atan计算。我使用了勾股+asin，可以少处理一些sc的角度问题。关于三角函数的使用以及正负转化，这里不多赘述，直接上代码：

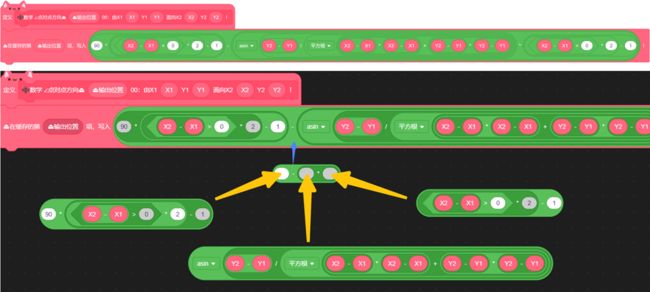
由 x1 y1 面向 x2 y2 的方向

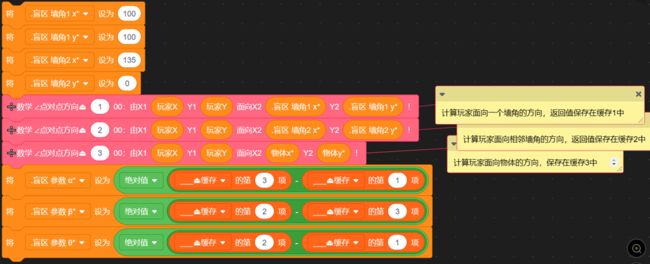
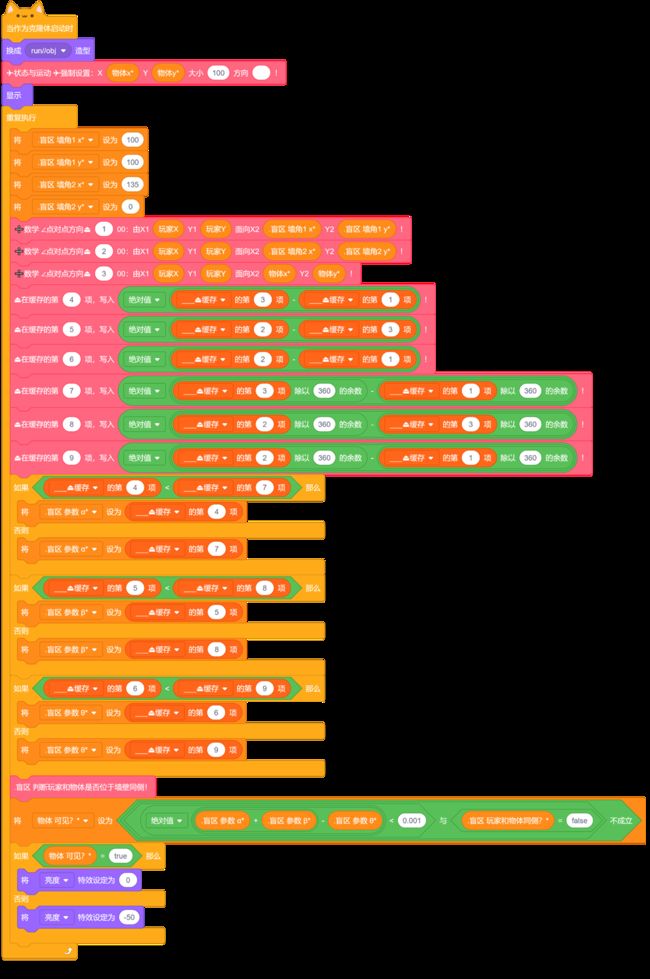
        那么，我们就可以写下这样的代码，来判断物体是否在盲区中：计算玩家面向一个墙角的方向，返回值保存在缓存1中；计算玩家面向相邻墙角的方向，返回值保存在缓存2中；计算玩家面向物体的方向，保存在缓存3中。然后分别将它们相减，算出α、β、θ的值，如下图：

计算α β θ

        接下来，如何判断α+β=θ？

        我们已经算出α、β、θ，不过值得一提的是，Scratch算数可不是那么准！好不容易算出的α、β、θ，他们的在精度上却很不幸地显出差异！本应相等的值，它们相差了0.00000000000001：

精度丢失

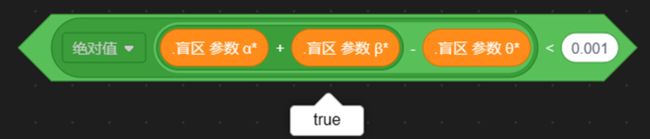
所以，我们应当避开这样的精度问题，做一点点小小的容错：将它们相减，得出它们相差的值，判断差是否很小，就如——

作差，进行精度容错

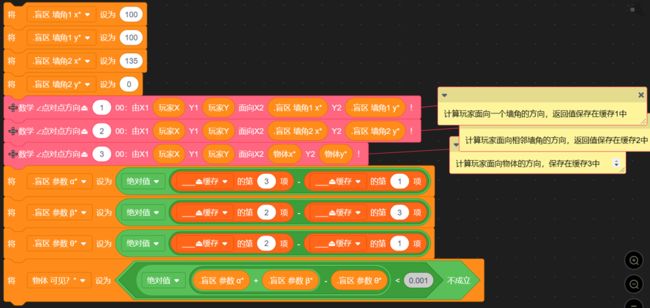
最后，把它作为物体是否可见的判断依据：

最后一块积木判断物体是否可见

Awesome！让我们来运行一下——（为了使程序更加直观，我连接了一些线段并延长，且显示出α、β、θ的大小（但是四舍五入了），实际的使用场景无需）：

成功了！

        恭喜，我们发现，程序已经可以根据位置来计算物体是否位于盲区中了！

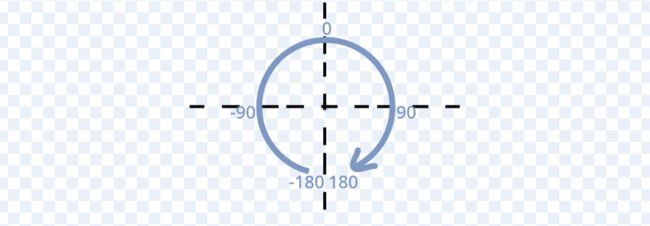
        可是……糟了，Scratch方向角度是从-180到180的，

Scratch方向

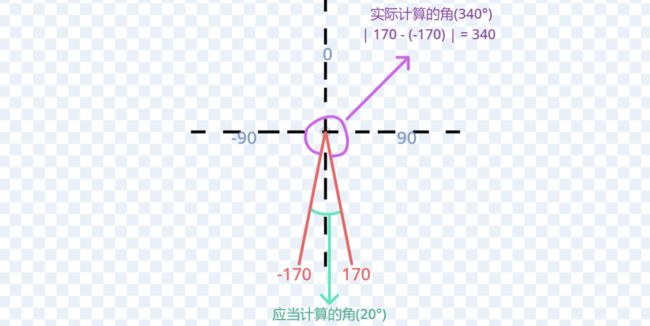
        也就是说，会有一种特殊情况——当我们要算-170方向的线与170方向的线，本结果应是20，却算出340：

角度计算错误

        让我们来处理一下这种情况

---

步骤3 | 处理Scratch角度制的特殊情况

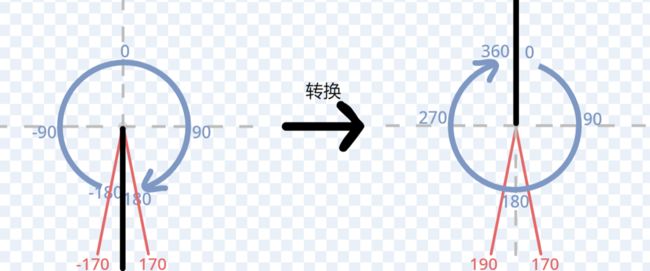
        之所以会把上面那个角算成340度，无非是因为Scratch的方向是从-180开始，180结束的。如果我们能让原本的-170变成190，即方向从0开始，360结束，那不就可以正确地计算出20°了吗？

        其实很简单，我们用：方向除以360的余数，就可以把所有奇奇怪怪的方向全都转换到0-360的区间：

        这样，我们就可以算出正确的20°：|170-190|=20。

        到了这里，可能有人就会问：“如果用你这个方法算20和-20(340)的角度差，本应该算出40，却又变成了|340-20|=320，不是会有一样的问题吗？”

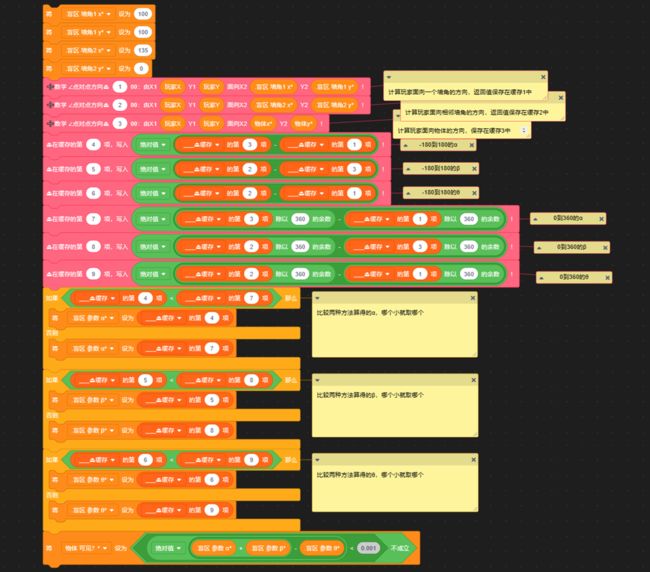
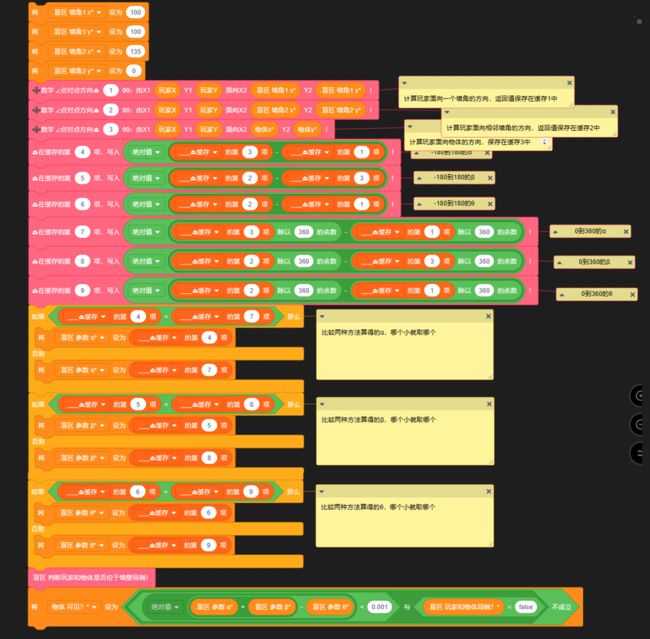
        没错。所以不管是什么角度，我们都用两种方法各计算一遍，哪个算得的角度差小，我们就取哪个：

        用两种方法各计算一遍，哪个算得的角度差小，我们就取哪个

        这样一来，我们就成功解决了Scratch中角度差的计算问题。

---

步骤4 | 判断玩家与物体 是否在墙面的同侧

        等等！是不是有一块位于夹角内的地方，也是可以看得见的呢？

        如下图，像这样的情况：

位于夹角内，但在墙前方的物体，是可见的！

---

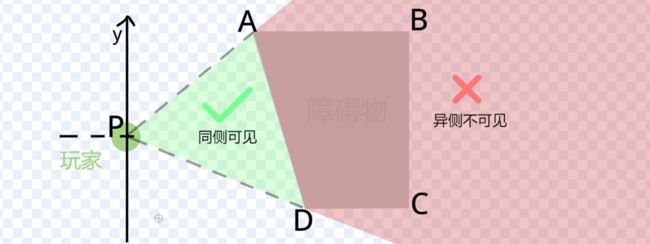
        判断一个点在夹角内之后，与玩家位于墙壁AD同侧的物体仍旧是可见的：

夹角内，同侧可见，异侧不可见

        要判断两点是否位于直线的同侧，使用一次函数是个不错的选择。

*提示：下方为推导过程，可直接空降到代码处

        设直线AD的解析式为：y=kx+b。A和D的坐标是已知的，我们就可以使用斜率公式：k=Δy/Δx，即 k = [ y(D) - y(A) ] / [ x(D) - x(A) ] 。现在还差常数项b未知，我们简单做个移项，把等式化为b=y-kx，然后把点A的坐标（D也可以）和刚刚算出的k代入b=y-kx，得到 b = y(A) - k*x(A)。现在，b和k都已经算出，AD的解析式就得到了。

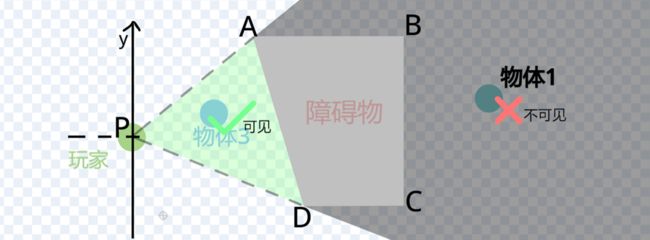
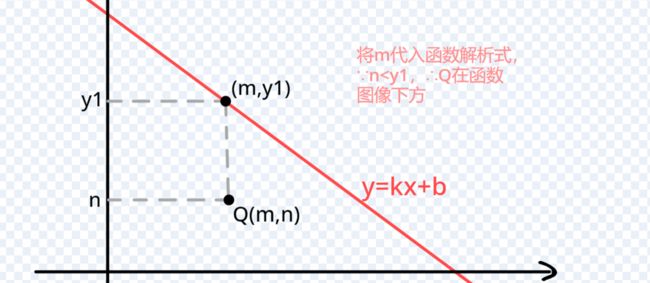
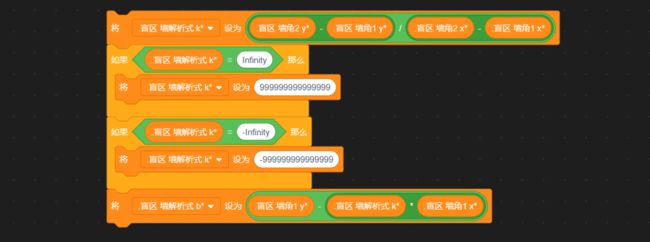
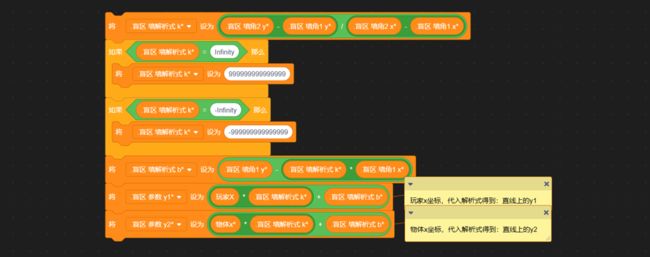
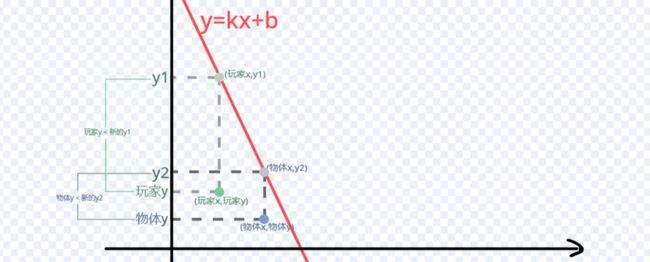
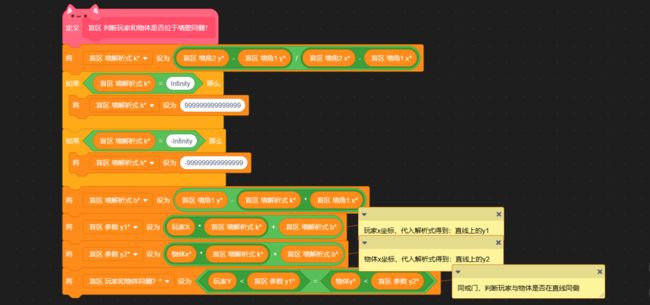
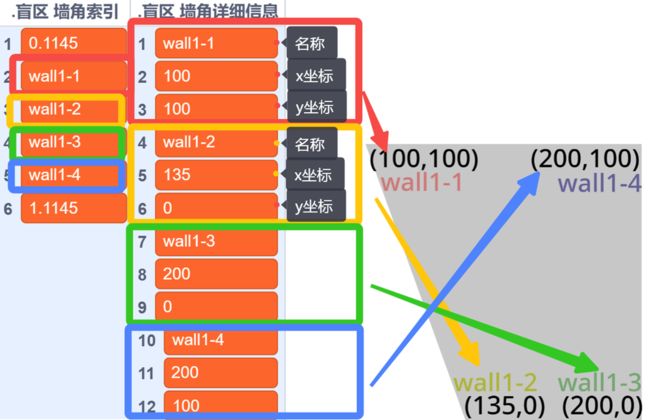
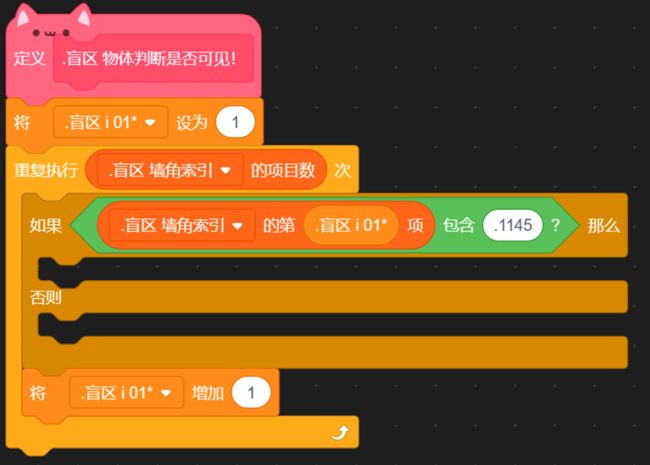
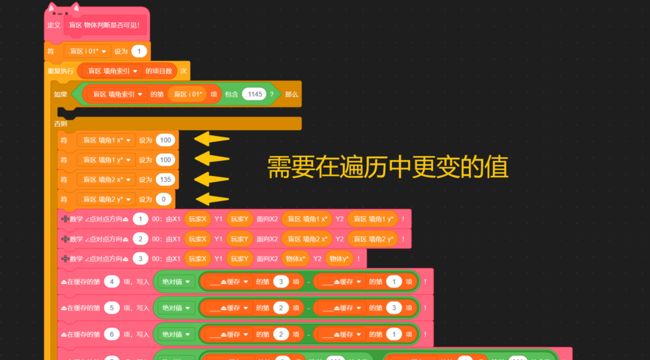
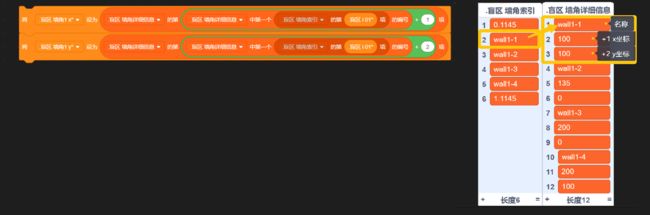
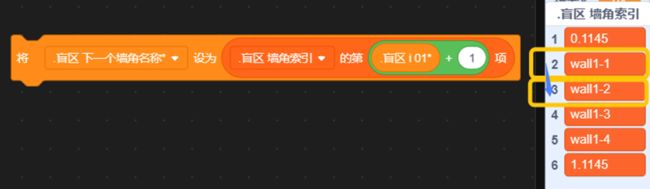
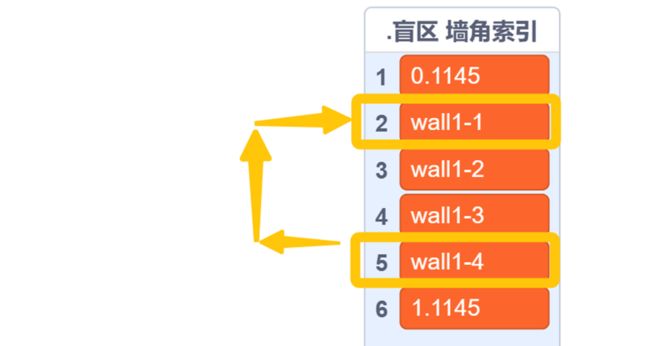
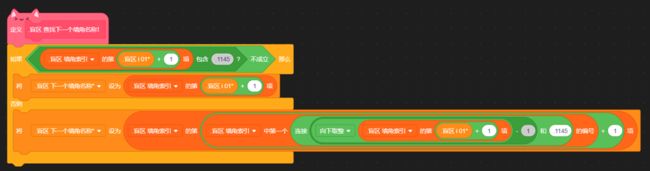
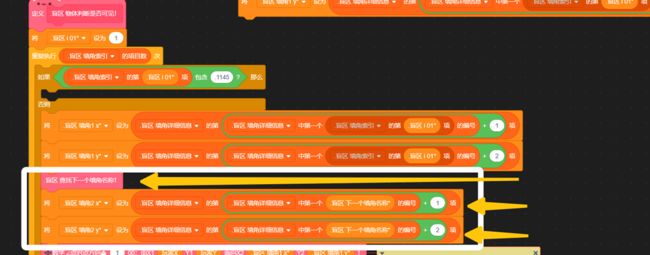
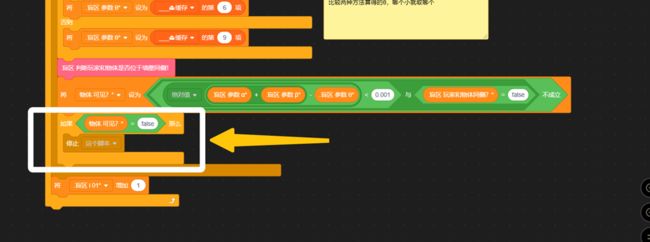
        初中数学我们学过，将平面直角坐标系中任意一点Q(m,n)的横坐标x=m代入函数解析式，会得到一个新的、唯一的y1值。若：n

        延长墙面AD。只需要判断：玩家与物体是否同时位于 墙壁所在直线AD的上方 或 是否同时位于下方 即可。

延长AD（红色直线）

*提示：接下来的代码有简化方案，但为方便理解，这里不做简化处理

        设AD:y=kx+b，根据上面的公式 k=Δy/Δx 和 b = y - kx ，计算出AD的解析式：

计算墙解析式中的参数k和b

        值得注意的是，当这条直线垂直于x轴的时候，斜率 k 的值将会是正负 Infinity 。这意味着，这条直线的参数 k 和 b 在接下来的运算中会出错，得到NaN。

        所以在算出 k 后，如果是±Infinity，我们需要将它转换成一个非常非常大的数，这样就能在误差极其微小（以致于忽略不计）的情况下，保证接下来的计算不会出错，如下：

斜率更正

        直线解析式已经解决。判断玩家和物体是否位于直线同侧，我们将玩家的x坐标和物体的x坐标分别代入解析式：y=kx+b

        得到直线上的y1和y2的实际意义如下图所示（以玩家和物体都在直线下方为例）：

        （图以玩家和物体都在直线下方为例）此时：玩家y小于y1，物体y小于y2，二者皆为小于，位于同侧，物体可见。

        （若玩家和物体都在直线上方）玩家y大于y1，物体y大于y2，二者皆为大于，位于同侧，物体可见。

        （若玩家和物体位于直线一上一下）玩家y小(大)于y1，物体y大(小)于y2，一个是大于，一个是小于，位于异侧，物体不可见。

        所以我们判断：<玩家y 小于 y1> 和 <物体y 小于 y2>。

        ①若两个都是true，则表示玩家和物体同在直线下方（同侧）；②若两个都是false，则表示玩家和物体都在直线上方（也是同侧）；③若一个true一个false，则表示玩家和物体：一个在直线上方，一个在直线下方（异侧）。

        所以我们将这两个条件放在等号中，若它们同是true或同是false，等号就会返回true，表示同侧；若它们一个是true一个是false，等号就会返回false，表示异侧。即同或。

        新建一个积木，名为判断同侧。将这些判断是否位于墙壁直线同侧的代码拼接起来，放在这个自制积木的定义中。

        最后，在判断物体是否可见的代码前，插入这个自制积木，然后在下方写入同侧可见异侧不可见：

        完美！把上面判断是否可见的代码段，放入克隆体的重复执行中。代码全览（部分自制积木已在上文出现或是本人习惯，下图未放出定义）：

        克隆出两个物体看看效果如何（连线是额外加的）：

        太棒了！

        和预想的效果一模一样，wonderful！

---

步骤5 | 添加、读取更多的墙

        这样的盲区肯定不能只有一面墙嘛！现在我们来添加更多的墙。

        创建两个列表，名为“墙角索引”和“墙角详细信息”：

        先来看列表“墙角索引”。这里需要存储的数据是：墙角的名称及顺序。因为要存储多组障碍物，我们需要在一个障碍物结束的位置加一个特殊标志（序号.1145）（序号是整数，第一个障碍物开始标识为0.1145，结束的标识为1.1145；同时1.1145也是第二个障碍物的开始标识）。

        墙角顺序的存储格式，可存储多组障碍物的墙角

        在另一个“墙角详细信息”的列表中，按照一定的格式，根据墙角名称，录入墙角位置：

存储方式

        现在，新建一个变量 i ，用于遍历 墙角索引：

        我们的目的是将每个墙角都遍历过去。当 i 指向列表中代表 墙角 的项时，正常计算是否可见；当 i 指向列表中代表 不同障碍物间标识符 的项（序号.1145）时，不进行任何操作。新建积木“物体判断是否可见”（！勾选“运行时不刷新屏幕”），在下方按照所需，接入遍历相关代码，如图：

        将克隆体循环中（除渲染部分）的代码，即判断是否可见的代码，放入“否则”分支里：

        通过遍历，我们需要改变的是当前墙角和逆时针相邻墙角的坐标值：

        需要改变 当前墙角（墙角1） 和 逆时针相邻墙角（墙角2） 的坐标值

        当前墙角的值可以这样读取：

        当前墙角坐标的读取方式

        下一个墙角的名称可以这样获取：

        相邻墙角名称的获取

        但是——若是末尾的墙角，比如 wall1-4 ，这样会读取到障碍物标识符（序号.1145），怎么办呢？

        这时候， .1145 前面的序号就起作用了。创建一个积木“读取相邻墙角名称”，在这里面放入读取代码。（若下一项不是标识符，即不包含.1145，则正常返回下一项的内容；若下一项是标识符，则需找到该障碍物的第一个墙角，要返回上一个标识符 (序号-1).1145 的项+1的墙角名称内容）。

        需要注意的是，不能直接用1.1145减去1得到0.1145，因为你得到的可能是0.11450000000000005。所以为了准确，上图先向下取整，-1，再连接.1145。

        接着，将这个获取名称的代码放入刚刚改变墙角2数据的前面，再从墙角详细信息中读取出坐标：

        别忘了在判断是否可见的位置后面加上：判断到false的时候，就立即停止继续判断（防止接下来的墙面又判断为可见）。

        停止自制积木，在第一次判断到false时就终止判断

        现在，我们来运行一遍：

运行效果（可见的亮，不可见的暗）

---

完成啦ヾ(^∀^)ﾉ！本方法所有代码如下图~

所有代码

        以上就是“区域判断法”的所有内容啦！

        阴影覆盖法，真的是超流畅的光线追踪好嘛！

        其实阴影覆盖法差不多啦~就是在区域判断法的基础上，把物体自判断删掉，然后一面一面墙绘制四边形阴影盖住而已。可以自己试试呀