【视觉SLAM入门】5.1. 特征提取和匹配--FAST,ORB(关键点描述子),2D-2D对极几何,本质矩阵,单应矩阵,三角测量,三角化矛盾
"不言而善应"
- 0. 基础知识
- 1. 特征提取和匹配
-
- 1.1 FAST关键点
- 1.2 ORB的关键点--改进FAST
- 1.3 ORB的描述子--BRIEF
- 1.4 总结
- 2. 对极几何,对极约束
-
- 2.1 本质矩阵(对极约束)
-
- 2.1.1 求解本质矩阵
- 2.1.2 恢复相机运动 R , t R,t R,t
- 2.1.3 本质矩阵调整
-
- 2.1.3 遗留问题
- 2.2 单应矩阵(特别提一下)
- 2.3 三角测量(Triangulation)---深度信息
为什么重要?我们是在做什么事?
- 特征提取和匹配: 首先是两幅图像的特征提取,然后是对应特征点的匹配。接下来的工作是根据得到的匹配点对,估计相机的运动,具体根据相机分为三种方法:
-
- 单目相机:2D-2D: 对极几何 方法
-
- 双目或者RGBD相机: 3D-3D: ICP 方法
-
- 一个3D点和它相机中的投影位置: 3D-2D : PnP 方法
0. 基础知识
视觉SLAM两阶段:
- 前端(VO) —> 粗略相机运动 ------> 提供给后端初始值
- 后端 —> 优化
VO的实现方法两派:
- 不提取特征点 ----> 直接法
- 提取特征点 ------> 特征点法 ----> 成熟
1. 特征提取和匹配
注意:有些东西的作用你要明白:
- 关键点: 是在一幅图像中找到的点,作用是在一幅图中找到路标点(有代表性的点)。
- 描述子: 在两个图像的关键点找到的情况下,匹配两个图像中的对应关键点。 通常是向量
- 特征点: 由关键点和描述子两部分组成,任务是(提取XXX关键点,计算XXX描述子)
- 尺度不变性: 为了确保从远到近都能检测出来关键点
- 旋转不变性: 为了确保图像旋转后还能检测出来关键点
- 特征提取的是关键点和描述子,特征匹配是根据描述子匹配的
几种图像特征:
- SIFT特征:计算量太大,有些精确
- FAST关键点:没有描述子,最快,不准。
- ORB特征:改进FAST关键点,采用BRIEF描述子
1.1 FAST关键点
-
- 比较周围半径圆范围内的灰度情况,差别大就是角点。
-
- 设定一个数量,比如9,范围内至少有连续9个点和选定点的亮度色差大于阈值T的时候,该点就称为特征点。这种方法叫FAST-9。
-
- 检测完角点扎堆,非极大值抑制
1.2 ORB的关键点–改进FAST
改进了FAST关键点法,克服了缺点:
-
- 可以指定提取数量: 对点分别计算Harris相应,取前N个响应最大的角点;
-
- 尺度不变性: 用图像金字塔提取每一层的角点,均为角点才是角点;
-
- 旋转不变性:灰度质心法,保证图像旋转后还能检测到。最后得到的是角度,从图像光度明指向光度暗的一侧,具体实现如下:
1.3 ORB的描述子–BRIEF
作用:为了保证两个图像中提取出的关键点能对应上各自匹配的点对。
- BRIEF是二进制描述子,描述向量由0和1组成
- 做法:选取关键点周围的图像块,随机选取像素点对(有很多选点方法),如128就是取128个点对,设两个点像素分别为 p , q p, q p,q , 然后计算 p , q p, q p,q 的大小关系,按结果分别记为0,1, 最后得到128位的二进制数。匹配的时候在第二幅图像中也用相同的选点方法,最后比较两幅图像中关键点描述子距离(二进制的字串衡量就是汉明距离)。
1.4 总结
通过图像特征点的对应关系,解决了SLAM最重要的一步:同一个点在不同图像中如何检测出来。
特征匹配的方法有:
- 暴力匹配(Brute-Force Matcher): 第二幅图像中每个点都计算其在第一幅图对应的特征点,运算量大;
- 快速最近邻(FLANN): 适用于匹配点数量多
- 。。。
2. 对极几何,对极约束
目的是求相机运动 R , t R, t R,t,内参一般知道
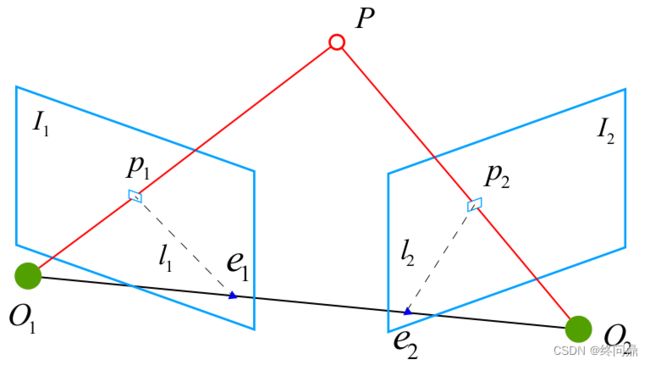
这是2D-2D的单目情形,假设相机经过一次运动 R , t R, t R,t 后得到的两帧图如下:
- p 1 , p 2 p_1,p_2 p1,p2 : 分别同一个点在两帧下的投影点
- O 1 , O 2 O_1, O_2 O1,O2 : 相机光心
- P P P : 真实世界中的点
- I 1 , I 2 I_1, I_2 I1,I2 : 两帧图像
- O 1 O 2 连线 O_1O_2连线 O1O2连线 : 基线
- e 1 , e 2 e_1, e_2 e1,e2 : O 1 O 2 O_1O_2 O1O2 和 I 1 , I 2 I_1,I_2 I1,I2 的交点,也叫极点
- 极平面 : O 1 , O 2 , P O_1,O_2,P O1,O2,P 所在平面
- 极线 : l 1 , l 2 l_1, l_2 l1,l2 。
如果没有深度信息,则 O 1 P O_1P O1P 直线上任一点投影都在 p 1 p_1 p1,且他在第二帧图像上的轨迹在 极线 p 2 e 2 p_2e_2 p2e2 上,所以有真确的匹配,就可以推断 P P P 的位置,然后得到相机的运动。
2.1 本质矩阵(对极约束)
推理部分略,详见《视觉SLAM十四讲》第七章7.3节,这里给出结果。
仍参考上图,取两个像素点归一化平面上的点 x 1 , x 2 x_1,x_2 x1,x2:
x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x_1=K^{-1}p_1,\qquad\qquad x_2 = K^{-1}p_2 x1=K−1p1,x2=K−1p2
则 最终的对极约束 为:
p 2 T K − T t \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad p_2^TK^{-T}t p2TK−Tt^ R K − 1 p 1 = 0 RK^{-1}p_1 = 0 RK−1p1=0
它的含义是 O 1 , O 2 , P O_1,O_2,P O1,O2,P 三点共面。从式中心部分,记本质矩阵 E \boldsymbol E E 和基础矩阵 F \boldsymbol F F 如下:
E = t \qquad\qquad\qquad\qquad\qquad\qquad\qquad E=t E=t^ R F = K − T E K − 1 x 2 T E x 1 = p 2 T F p 1 = 0 R\qquad\qquad F=K^{-T}EK^{-1}\qquad\qquad x_2^TEx_1=p_2^TFp_1=0 RF=K−TEK−1x2TEx1=p2TFp1=0
可以看出 E \boldsymbol E E 和 F \boldsymbol F F 只差内参 K K K (已知),所以二者 求一即可。
不妨以 E = t E=t E=t^ R R R来求解。则后续工作如下:
- 根据已匹配点对,求出 E \boldsymbol E E或 F \boldsymbol F F
- 根据 E \boldsymbol E E或 F \boldsymbol F F,求出相机运动 R , t \boldsymbol {R,t} R,t
2.1.1 求解本质矩阵
探究本质矩阵的特点:
-
- 由对极约束 x 2 T E x 1 = 0 x_2^TEx_1=0 x2TEx1=0 , 所以它在不同尺度下等价,左右乘依旧满足约束。又因为 E = t E=t E=t^ R R R, 原本有6个自由度,故去掉尺度,还有5个自由度
-
- E 的内在性质 E的内在性质 E的内在性质 : 它的奇异值必定是 [ δ , δ , 0 ] T [\delta ,\delta, 0]^T [δ,δ,0]T 的形式,非线性的性质。
求解依据:
x 2 T E x 1 = 0 ( 1 ) x_2^TEx_1 = 0 \qquad\qquad\qquad\qquad (1) x2TEx1=0(1)
理论上可以用5对点来求解,但是很麻烦。故用 八点法 求解(由于尺度不变性)。
1.首先考虑一对点(归一化坐标 x 1 , x 2 x_1, x_2 x1,x2 ): 将(1)式展开:
( u 1 , v 1 , 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) ( u 2 v 2 1 ) = 0 ⇓ 将 e 展开 e = [ e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 , e 9 ] ⇓ 展开并重写 [ u 1 u 2 , u 1 v 2 , u 1 , v 1 u 2 , v 1 v 2 , v 1 , u 2 , v 2 , 1 ] ⋅ e = 0 ⇓ 考虑 8 对点的方程组 (u_1, v_1,1)\begin{pmatrix} e_1\quad e_2\quad e_3 \\e_4\quad e_5\quad e_6 \\e_7\quad e_8\quad e_9 \end{pmatrix}\begin{pmatrix} u_2\\v_2\\1 \end{pmatrix}=0 \quad\\\; \\\;\Downarrow 将e展开 \\\;\\\;e=[e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9]\\\;\\\; \Downarrow展开并重写\\\;\\\; [u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]\cdot e = 0 \\\;\\\Downarrow考虑8对点的方程组 (u1,v1,1) e1e2e3e4e5e6e7e8e9 u2v21 =0⇓将e展开e=[e1,e2,e3,e4,e5,e6,e7,e8,e9]⇓展开并重写[u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]⋅e=0⇓考虑8对点的方程组

至此,本质矩阵的求解结束
2.1.2 恢复相机运动 R , t R,t R,t
- 对 E \boldsymbol E E 做SVD分解
E = U ∑ V T ( U , V 正交阵, ∑ 为奇异矩阵且 = d i a g ( δ , δ , 0 ) ) E=U\sum V_T\qquad\qquad (U,V正交阵,\sum 为奇异矩阵且=diag(\delta,\delta,0)) E=U∑VT(U,V正交阵,∑为奇异矩阵且=diag(δ,δ,0)) - 求解较为复杂,这里给出结果
 一共存在4组解。如下:
一共存在4组解。如下:

蓝色横线就是相机平面,红色点为投影点。
有(1)满足要求,因为只有这样才符合投影模型,深度才为正。将解出来的解带入验算即可。
2.1.3 本质矩阵调整
5个自由度,用了8个点,上边的方程求解出的 E E E 可能不满足 E E E 的内在性质( ∑ = d i a g ( δ , δ , 0 ) \boldsymbol {\sum = diag(\delta,\delta,0)} ∑=diag(δ,δ,0) ),因此要调整。做法如下:
在做SVD分解时,得到
∑ = d i a g ( δ 1 , δ 2 , δ 3 ) ⇓ 设 δ 1 ≥ δ 2 ≥ δ 3 ,则新的 ∑ 如下 ∑ ′ = d i a g ( δ 1 + δ 2 2 , δ 1 + δ 2 2 , 0 ) ⇓ 带入 S V D 分解式 E = U d i a g ( δ 1 + δ 2 2 , δ 1 + δ 2 2 , 0 ) V T \sum = diag(\delta_1,\delta_2,\delta_3) \\\;\\\Downarrow 设\delta_1\ge\delta_2\ge\delta_3,则新的\sum如下\\\; \\\sum' = diag(\frac{\delta_1+\delta_2}{2}, \frac{\delta_1+\delta_2}{2},0)\\\; \\\Downarrow 带入SVD分解式\\\; \\E=Udiag(\frac{\delta_1+\delta_2}{2}, \frac{\delta_1+\delta_2}{2},0)V^T ∑=diag(δ1,δ2,δ3)⇓设δ1≥δ2≥δ3,则新的∑如下∑′=diag(2δ1+δ2,2δ1+δ2,0)⇓带入SVD分解式E=Udiag(2δ1+δ2,2δ1+δ2,0)VT
相当于把求出来的矩阵投影到了 E \boldsymbol E E 的流形上,也可以直接取 ∑ = ( 1 , 1 , 0 ) \sum = (1,1,0) ∑=(1,1,0) (尺度不变性)
2.1.3 遗留问题
- E \boldsymbol E E 的尺度不确定性导致了 t \boldsymbol {t} t 的尺度不确定性。(由于 R \boldsymbol R R) 自身带有约束。因此单目SLAM存在初始化: 以 t \boldsymbol t t 的单位为固定尺度1的计算相机运动和特征点;
- 单目初始化不能只有纯旋转,必须要有一定的平移: 因为 t \boldsymbol t t 为0,所以 E \boldsymbol E E 最终也为0;
- 当点多于8对,此时构成超定方程,我们有两种做法:
- 3.1. 最小化一个二次型(最小二乘意义下的)
- 3.2. 随机采样一致性(RANSAC),可以处理有错误匹配的情况,一般用这个。
2.2 单应矩阵(特别提一下)
为什么需要单应矩阵 H H H (Homography)?
- 当特征点共面,相机纯旋转, F \boldsymbol F F 的自由度少了 t t t ,下降。这就是退化现象。
- 如果这时仍用八点法求解,多出来的自由度是噪声带来的。
- 为了避免退化,同时估计基础矩阵 F \boldsymbol F F 和 单应矩阵 H \boldsymbol H H,选择重投影误差小的矩阵作为最终运动估计矩阵。
故 H H H 假设的所有特征点位于平面上。
详细推导内容见SLAM十四讲7.3.3 。根据法平面做的,求解与 E 和 F E和F E和F 相似。只需要4对匹配点就可以算出。
2.3 三角测量(Triangulation)—深度信息
-
计算深度:回想相机模型那一节,这里的深度就是之前被我们固定为1的 s \boldsymbol s s 。以第一帧图像为坐标原点,由以上对极约束内容有:
s 1 x 1 = s 2 R x 2 + t ⇓ 分别单独计算,左乘 x 1 的反对称矩阵 s_1x_1 = s_2Rx_2+t \\\; \\\Downarrow 分别单独计算,左乘x_1的反对称矩阵 s1x1=s2Rx2+t⇓分别单独计算,左乘x1的反对称矩阵
s 1 ( x 1 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad s_1(x_1 s1(x1^ ) x 1 = 0 = s 2 ( x 1 )x_1=0=s_2(x_1 )x1=0=s2(x1 ^ ) R x 2 + ( x 1 )\;Rx_2+(x_1 )Rx2+(x1 ^ ) t )t )t -
可以直接求得深度 s 1 , s 2 \boldsymbol {s_1,s_2} s1,s2 。但是由于噪声的存在,我们一般是求最小二乘解,而不是零解。同样由于尺度不确定性,我们只知道深度对于t的数量,而不知道具体究竟是多少米。
-
三角化矛盾: 平移越大三角化越精确,但是视野越短,反之亦然。