20220906美的集团笔试

20220906美的集团笔试

第一题 杨辉三角

题目链接

• https://leetcode.cn/problems/pascals-triangle/

题目描述

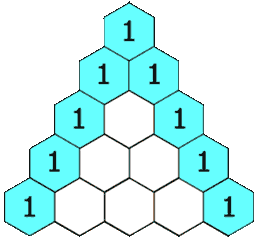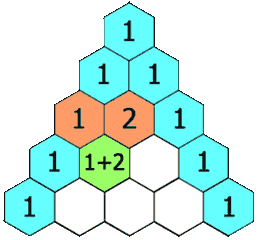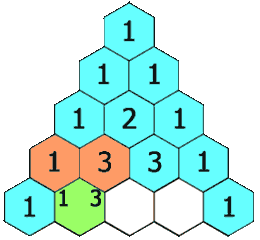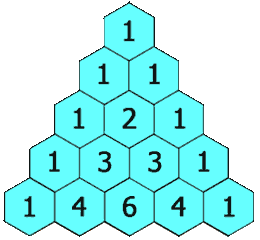
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

• 1 <= numRows <= 30

解题思路

按照杨辉三角的性质做就行

AC代码

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; i++) {
            List<Integer> row = new ArrayList<>();
            for (int j = 0; j <= i; j++) {
                if (j == 0 || j == i)
                    row.add(1);
                else
                    row.add(ans.get(i - 1).get(j - 1) + ans.get(i - 1).get(j));
            }
            ans.add(row);
        }
        return ans;
    }
}

第二题 直线上最多的点数

题目链接

• https://leetcode.cn/problems/max-points-on-a-line/

题目描述

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例 1：

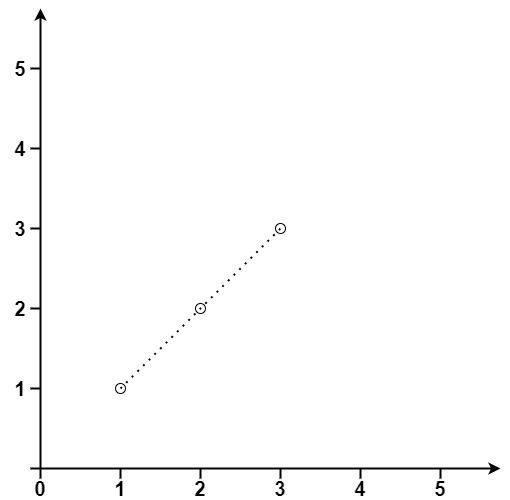
输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例 2：

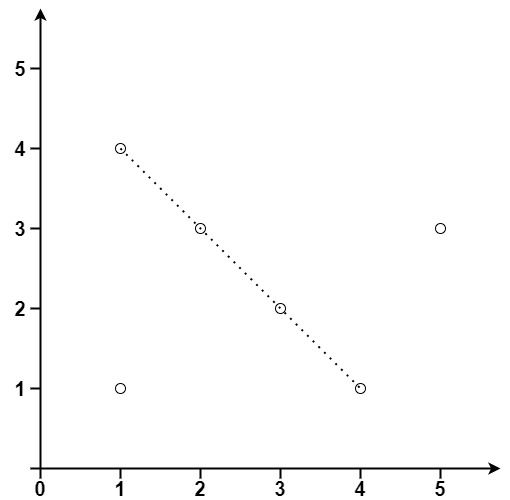
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

提示：

• 1 <= points.length <= 300
• points[i].length == 2
• -10^4 <= xi, yi <= 10^4
• points 中的所有点 互不相同

解题思路

我们知道，两个点可以确定一条线。

因此一个朴素的做法是先枚举两条点（确定一条线），然后检查其余点是否落在该线中。

为了避免除法精度问题，当我们枚举两个点 i 和 j 时，不直接计算其对应直线的 斜率和 截距，而是通过判断 i 和 j 与第三个点 k 形成的两条直线斜率是否相等（斜率相等的两条直线要么平行，要么重合，平行需要 4 个点来唯一确定，我们只有 3 个点，所以可以直接判定两直线重合）。

AC代码

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        int ans = 1;
        for (int i = 0; i < n; i++) {
            int[] x = points[i];
            for (int j = i + 1; j < n; j++) {
                int[] y = points[j];
                int cnt = 2;
                for (int k = j + 1; k < n; k++) {
                    int[] p = points[k];
                    int s1 = (y[1] - x[1]) * (p[0] - y[0]);
                    int s2 = (p[1] - y[1]) * (y[0] - x[0]);
                    if (s1 == s2) cnt++;
                }
                ans = Math.max(ans, cnt);
            }
        }
        return ans;
    }
}