快速排序——“数据结构与算法”
各位CSDN的uu们好呀,今天又是小雅兰的数据结构与算法专栏啦,下面,就让我们进入快速排序的世界吧!!!
快速排序
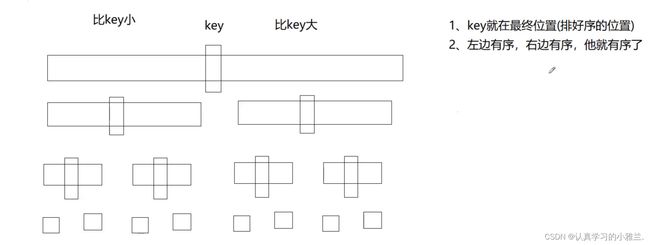
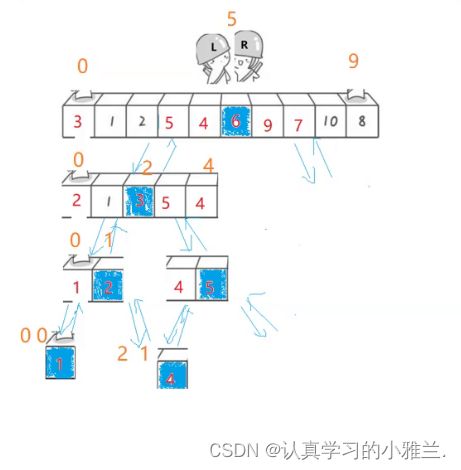
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右 子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
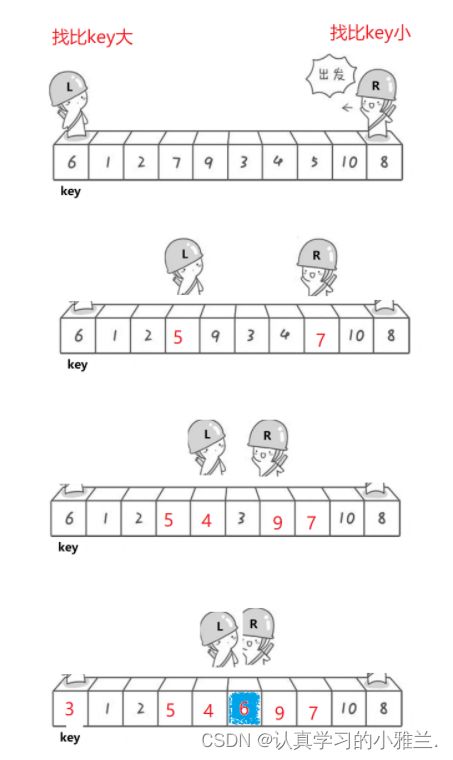
hoare法

//hoare法 int PartSort1(int* a, int left, int right) { int keyi = left; while (left < right) { //右边找小 //要防止死循环和越界的问题 while (left < right && a[right] >= a[keyi]) { --right; } //左边找大 while (left < right && a[left] <= a[keyi]) { ++left; } Swap(&a[left], &a[right]); } Swap(&a[left], &a[keyi]); return left; } void QuickSort(int* a, int begin, int end) { if (begin >= end) { return; } int keyi = PartSort1(a, begin, end); //[begin,keyi-1] keyi [keyi+1,end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); }测试一下快速排序:
void TestQuickSort()
{
int a[] = { 2,1,4,3,6,5,7,9,8,10 };
PrintArray(a, sizeof(a) / sizeof(a[0]));
QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
这边有一个问题
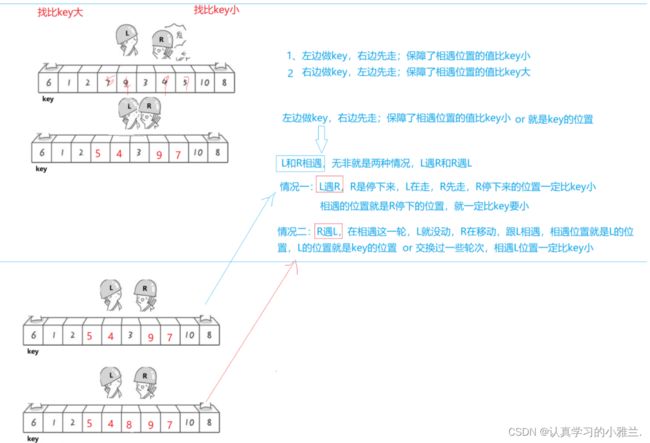
如何保证left和right相遇的位置一定比keyi小呢?
左边作keyi,右边先走,保障了相遇位置的值比keyi小或者是就是keyi的位置
left和right相遇,无非就是两种情况,left遇right和right遇left
情况一:left遇right,right是停下来,left在走。right先走,right停下来的位置一定比keyi小,相遇的位置就是right停下来的位置,就一定比keyi小。
情况二:right遇left,在相遇这一轮,left就没动,right在移动,跟left相遇,相遇位置就是left的位置,left的位置就是keyi的位置,或者交换过一些轮次,相遇left的位置一定比keyi小
右边作keyi,左边先走,保障了相遇位置的值比keyi大
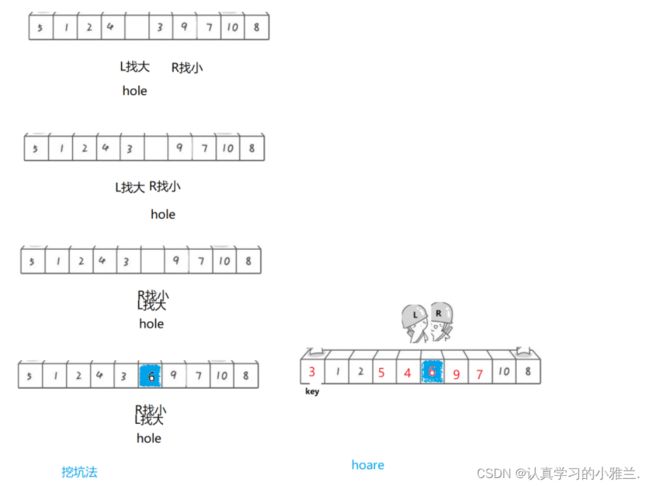
挖坑法
//挖坑法 int PartSort2(int* a, int left, int right) { int key = a[left]; int hole = left; while (left < right) { //右边找小 //要防止死循环和越界的问题 while (left < right && a[right] >= key) { --right; } a[hole] = a[right]; hole = right; //左边找大 while (left < right && a[left] <= key) { ++left; } a[hole] = a[left]; hole = left; } a[hole] = key; return hole; } void QuickSort(int* a, int begin, int end) { if (begin >= end) { return; } int keyi = PartSort2(a, begin, end); //[begin,keyi-1] keyi [keyi+1,end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); }
前后指针法
//前后指针法 int PartSort3(int* a, int left, int right) { int prev = left; int cur = left + 1; int keyi = left; while (cur <= right) { if (a[cur] < a[keyi]) { ++prev; Swap(&a[prev], &a[cur]); } ++cur; } Swap(&a[prev], &a[keyi]); keyi = prev; return keyi; } void QuickSort(int* a, int begin, int end) { if (begin >= end) { return; } int keyi = PartSort3(a, begin, end); //[begin,keyi-1] keyi [keyi+1,end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); }
快速排序优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
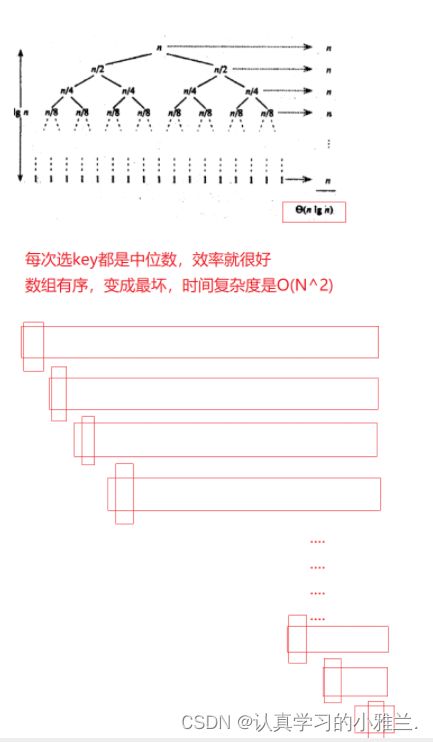
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
三数取中:
int GetMidIndex(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] < a[mid]) { if (a[mid] < a[right]) { return mid; } else if (a[left] < a[right]) { return right; } else { return left; } } else // a[left] > a[mid] { if (a[mid] > a[right]) { return mid; } else if (a[left] > a[right]) { return right; } else { return left; } } }
优化后的所有方式源代码:
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
// hoare
// [left, right]
int PartSort1(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);int keyi = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[keyi])
{
--right;
}// 左边找大
while (left < right && a[left] <= a[keyi])
{
++left;
}Swap(&a[left], &a[right]);
}Swap(&a[keyi], &a[left]);
return left;
}
// 挖坑法
// [left, right]
int PartSort2(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);int key = a[left];
int hole = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= key)
{
--right;
}a[hole] = a[right];
hole = right;// 左边找大
while (left < right && a[left] <= key)
{
++left;
}a[hole] = a[left];
hole = left;
}a[hole] = key;
return hole;
}// 前后指针法
// [left, right]
int PartSort3(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}++cur;
}Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort3(a, begin, end);
//[begin,keyi-1] keyi [keyi+1,end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
快速排序非递归
void QuickSortNonR(int* a, int begin, int end) { Stack st; StackInit(&st); StackPush(&st, end); StackPush(&st, begin); while (!StackEmpty(&st)) { int left = StackTop(&st); StackPop(&st); int right = StackTop(&st); StackPop(&st); int keyi = PartSort1(a, left, right); // [left, keyi-1] keyi [keyi+1, right] if (keyi + 1 < right) { StackPush(&st, right); StackPush(&st, keyi + 1); } if (left < keyi - 1) { StackPush(&st, keyi - 1); StackPush(&st, left); } } StackDestroy(&st); }测试一下快速排序非递归:
void TestQuickSortNonR()
{
int a[] = { 2,1,4,3,6,5,7,9,8,10 };
PrintArray(a, sizeof(a) / sizeof(a[0]));
QuickSortNonR(a, 0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
Stack.h和Stack.c的内容:
#pragma once #include#include #include #include typedef int STDataType; typedef struct Stack { STDataType* a; int top;//栈顶 int capacity;//容量 }Stack; // 初始化栈 void StackInit(Stack* pst); // 销毁栈 void StackDestroy(Stack* pst); // 入栈 void StackPush(Stack* pst, STDataType x); // 出栈 void StackPop(Stack* pst); // 获取栈顶元素 STDataType StackTop(Stack* pst); // 获取栈中有效元素个数 int StackSize(Stack* pst); // 检测栈是否为空 bool StackEmpty(Stack* pst); #include"Stack.h" // 初始化栈 void StackInit(Stack* pst) { assert(pst); pst->a = NULL; pst->top = 0; pst->capacity = 0; } // 销毁栈 void StackDestroy(Stack* pst) { assert(pst); free(pst->a); pst->a = NULL; pst->top = pst->capacity = 0; } // 入栈 void StackPush(Stack* pst, STDataType x) { assert(pst); //扩容 if (pst->top == pst->capacity) { int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2; STDataType* tmp = (STDataType*)realloc(pst->a, newcapacity * sizeof(STDataType)); if (tmp == NULL) { perror("realloc fail"); return; } pst->a = tmp; pst->capacity = newcapacity; } pst->a[pst->top] = x; pst->top++; } // 检测栈是否为空 bool StackEmpty(Stack* pst) { assert(pst); if (pst->top == 0) { return true; } else { return false; } //return pst->top==0; } // 出栈 void StackPop(Stack* pst) { assert(pst); assert(!StackEmpty(pst)); pst->top--; } // 获取栈顶元素 STDataType StackTop(Stack* pst) { assert(pst); assert(!StackEmpty(pst)); return pst->a[pst->top - 1]; } // 获取栈中有效元素个数 int StackSize(Stack* pst) { assert(pst); return pst->top; }
好啦,小雅兰的快速排序的所有的内容就到这里啦,还要继续加油学数据结构与算法啦,敬请期待小雅兰下一篇的归并排序的内容!!!