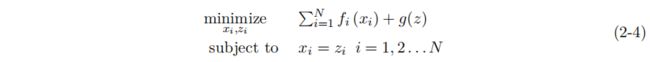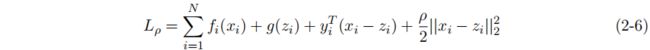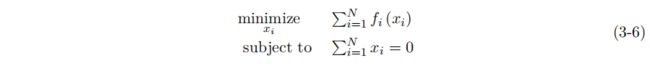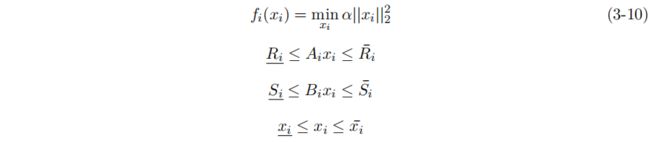开源代码分享(10)—基于ADMM算法的电动汽车群体充电优化(附matlab代码)

1.引言

        电动汽车是汽车行业中快速增长的市场。此外，广泛使用可再生能源来驱动电动汽车使其具备可持续性，并且温室气体排放极低。因此，服务提供商正在转向使用电动车队推广环境可持续性。然而，与传统车辆不同，电动汽车需要独特的基础设施来给它们充电，这带来了一些技术和经济上的挑战。因此，需要采用智能充电策略来对电动车队进行最优充电。

        该论文的主要目标是通过采用不同的充电策略，最小化电动车队运营商的能源和电池退化成本。为了实现这一目标，采用了联合优化技术来解决问题。采用的方法是一种通过清除市场约束条件的最优交换问题。具体而言，采用基于ADMM的分布式充电问题来对电动车队进行充电。该算法针对不同策略的不同充电功率水平进行实现，以分析能源和电池退化成本的差异。此外，还提出了一种变量充电器分配方法来充电电动车队。

2.ADMM算法

        在本节中，我们将介绍ADMM方法。ADMM算法结合了对偶上升的可分解性和乘子器方法的收敛性。ADMM是一种通常用于求解可分离函数的凸优化算法。然而，它也可以优化相当非光滑的凸函数。此外，在[5]中给出的广义问题公式可以应用于大多数问题。

 其中，变量x∈Rl，z∈Rn。函数f和g是凸的。这些函数受到一个线性等式约束，其中a∈Rp∗l，B∈Rp∗n和c∈Rp。采用了乘数法。因此，我们将增广拉格朗日量视为：

其中Lρ是增广拉格朗日数。解决该问题所需的迭代方法如下：

        其中，ρ > 0。ADMM算法与对偶上升和乘子的方法非常相似。在乘子法中，拉格朗日量与两个原变量一起最小化。然而，在ADMM中，变量x和z是交替更新的或顺序更新的，考虑了交替方向项[5]。它可以看作是在变量x和z上的高斯-塞德尔迭代，而不是联合最小化。这两个变量的分离对于分解函数f和g是必要的。然后使用下一个状态x k+1和z k+1来更新变量y。下一节演示了解决ADMM交换问题的一个直接的解决方案。

        本文认为电动汽车车队充电是一个交换问题。本节将解释共享问题的解决方案。式（3-6）中的共享问题有一个共享的目标g，它是集合{0}的一个指标。向量xi的组成部分表示在N个代理[5]之间交换的商品的数量。因此，将等式（3-6）中给出的交换问题重新表述为[5]：

 再看方程（2-4）和方程（3-6），我们可以说这两个公式是相同的。因此，为了解决这个问题，我们首先定义了一个增广的拉格朗日函数[24]。

 其中，ρ为增广项的惩罚参数。增广项通过取弗罗比尼乌斯范数的平方，对原变量x和z引入了一个惩罚。y=[y1，y2…]的转置是拉格朗日变量的向量。该函数在原变量xi和zi上最小，在拉格朗日变量yi上最大。

拉格朗日方程（2-6）的求解方法为方程（2-8） 

然后用方程（2-6）中的拉格朗日函数展开。项x表示商品x的初始值向量，x k+1是商品的更新值向量。

因此，方程式（2-9）被迭代求解。首先，通过最小化拉格朗日函数来计算x的更新。然后，用更新后的x变量计算z更新。最后，我们通过x和z的更新来最大化变量y。因此，求解这些迭代，我们得到以下公式，它给出了与方程（3-6）中的交换问题相同的解。

利用上述方程求解了ADMM交换问题的数学解。

3.电动汽车最优充电策略

3-1成本最小化问题

本文所考虑的问题是一个作为联合优化问题设计的车队充电问题。电动汽车车队充电有两个组成部分：聚合器和电动汽车。聚合器希望将使用电网能源的价格向车队充电的成本降至小化，而个别电动汽车希望将其退化成本降小化。在本文中，一个私人船队的运营商希望将总成本最小化。然而，在聚合器的视角和电动汽车的充电视角之间总是存在一种权衡。因此，提出了一个联合优化问题[24]。

优化变量x为充电功率。因此，xa是整个舰队每天的每个时间段的功率配置文件。Xi是当天的个人电动汽车的功率配置文件。现在，让我们考虑一下，如果xi (t) > 0，汽车在t时刻充电。同样，如果xi (t) <为0，则认为在t时刻放电。对于聚合的EV轮廓xa也可以这样考虑。因此，考虑到电动汽车的数量和聚合器的组合，我们重新表述了这个问题。聚合器和电动汽车被认为是代理： 

聚合器被认为是第n个代理。直观地看，聚合器花费能量给汽车充电，可以被认为是放电能量。

 第N个代理的成本函数为：

电动汽车的成本函数为： 

因此，车队充电问题可以被改写为一个交换问题：

交换问题考虑了N个代理在平衡约束[5]下交换一个共同的目标。变量x∈，=1…N.fi是子系统i的成本函数。在初步工作中讨论了交换问题的表述。下一节说明了电动汽车车队充电的分配模型。 

 3-2最优车队充电问题的优化模型

最优电动汽车管理问题分别解决了聚合器和个别电动汽车问题。然而，它们是通过更新信号和公式（3-6）中提到的交换问题约束来连接的。因此，计算公式如下：对于每个EVi=1,2…N-1[25]：

式中，ρ表示增广拉格朗日函数中的惩罚项。来自聚合器的激励信号表示每次迭代的平均功率不匹配。交换ADMM问题被认为是一个具有价格调整过程[1]的一般均衡问题。因此，每个电动汽车代理商都希望最小化其能耗xi，以最小化个人成本fi（xi）。按成本进行调整。 

3-3电动汽车优化模型

电池是电动汽车的重要组成部分。锂电池是电动汽车的主要候选电池，因为它们的高功率密度和更高的循环寿命[29]。尽管锂电池有良好的生命周期，但锂电池的退化是电动汽车车队车主面临的重大问题之一。电池充放电越多，降解程度就越多。目前，关于提高电池寿命的研究还很广泛。在本文中，我们试图使用一个模型来描述电动汽车电池的老化成本，并以优化变量作为从充电器中提取的功率。充电器的额定功率决定了电动汽车充电的速度。如果充电器功率过高，则充电速度越快。因此，为了建立这个模型，我们考虑了一个二次关系。随着时间的推移，电池会随着充电电量的平方而下降。因此，方程（3-7）中的电动汽车的成本函数由[25]给出：

 第一个不等式Ri≤Aixi≤¯Ri，设置了EV在每次连接时所需的最小能量的定界。所需的能量取决于电动汽车的驾驶状况和充电策略。第二个约束条件，Si≤Bixi≤S¯i，决定了电动汽车电池的状态方程。它保证电池的状态保持在一个运行水平。它决定了可以投入到电池或移除电池的能量。最后一个约束，xi≤xi≤x¯i确定所绘制的最小和最大功率。个人电动汽车的优化是基于他们的个人目标和激励信号。比例变量u可以被认为是聚合器为电动汽车定义的能源价格。用¯x表示的优化变量x的平均值可以被认为是由于电动汽车不协同实现全局收敛而造成的社会成本。个别电动汽车优化会考虑到这些价格。个别电动汽车优化模型如下：

 4算例分析

在我们的模拟设置中，我们考虑由一个车队运营商管理的40辆电动汽车车队。电动汽车在一天内行驶的最大距离约为300公里。由于电动汽车行驶1公里需要大约0.45-0.65 kWh的能量，最大距离对应250 kWh的能量需求时。为了考虑电动汽车应该执行的驾驶任务的不确定性程度，我们在1至250千瓦时的范围内，随机生成了电动汽车的100个能源需求曲线的均匀分布。此外，我们在仿真中考虑了不同的功率充电水平。四个充电器的额定功率分别为5 kW、16 kW、25 kW和40 kW然而，在第二种情况下，电动汽车被连接到电网上两次。模拟设置具有相同的舰队大小。

然而，在这种情况下，产生了两个单独的能量需求。因此，我们考虑每次的最大能量范围为125千瓦时。在这种情况下，我们在四种不同的功率水平上实施两种充电策略，并分析相关成本，以获得为车队运营商找到有利的策略。公式（3-8）中给出的聚合器优化是根据当天的能源价格对聚合器能量进行优化的。一天的能源价格概况如图（5-1）所示。

由车队运营商管理的电动汽车主要在白天开车，晚上返回电动汽车中心。因此，夜间充电是指电动汽车在夜间连接到电网的情况。这些电动汽车只连接到电网一次。在这种情况下，唯一可能的充电方法是贪婪的。第二章解释了贪婪收费方法的定义。电动汽车连接电网8小时，如驱动轮廓（5-2）所示。当电动汽车连接到电网时，下一次旅行所需的能量必须一次性提供。

 在本节中，我们对100个随机产生的能量需求场景进行了模拟，并使用5 kW、16 kW、25 kW和40 kW四种不同的功率级充电器给电动汽车充电。

在图（5-3）中，显示了各种充电器的各个电动汽车满意场景的百分比。例如，使用5 kW充电器，只有7-20%的能源需求场景被个别电动汽车所满足。这是因为5 kW充电器只能提供40千瓦时8小时。因此，这表明近80-90%的场景的能量需求大于40kWh，一个5 kW的充电器不满足要求。此外，随着更高的充电器功率，如16 kW和25 kW，在满意的场景中增加了20-60%。在这里，只有40 kW的充电器满足100%情况的能源需求。这一分析本身就表明，使用最高功率水平的充电器可以更好地安全地满足预期的需求。然而，这在电池退化方面是昂贵得多的，接下来要分析。

为了比较退化和聚合器的成本，我们现在考虑一个场景，其中所有的充电器都满足能源需求。在这种情况下，假设所有电动汽车的能量需求的最大范围为40千瓦时。然后进行仿真，并观察到结果。图（5-4）显示了基于充电器类型的各个电动汽车所产生的退化成本。如预期的那样，充电器的额定功率与电池的退化直接相关。例如，如果我们考虑EV数字7、8和31，就会有明显的退化增加，这是因为即使能量需求是相同的，在特定时间投入到电动汽车中的能量也是不同的。因此，如果在特定的时间给电动汽车投入更多的能量来充电更快，它的降解程度就越大。电动汽车车队的全部退化成本见表（5-1）。有趣的是，由于更高功率水平的充电器可以在较低的能源价格期间投入更多的能量，从而给聚合器带来更低的成本。然而，由于更高的电池退化，使用高功率充电器充电的总成本很高。

图（5-5）显示了整个优化期间电动汽车的聚合能源需求。我们假设电网在任何一小时都能提供的最大能量约为600千瓦时。该聚合器向电动汽车收费，以最小化能源价格。因此，它试图尽量减少高价格的收费。我们注意到，在07点到16点之间，电动汽车没有连接到充电站。在这里，从00：00到02：00，能源价格很低，如图（5-1）所示，因此最大的能源消耗。因此，如果充电器具有更高的额定功率，它可以以更低的价格投入更多的能源，以显著降低聚合器的成本。同样需要注意的是，如果一个低功率的充电器能够满足能源需求，那么它对电网的压力就会更小，使其在高电动汽车渗透率的情况下有利于电网运营商。车队的聚合成本见表（5-1）所示。

 

车队退化一词是指车队中所有电动汽车的电池退化。此外，聚合器成本是使用电网能源所支付的价格。表（5-1）显示了机队退化、聚合器和机队产生的总成本。此外，一个较低等级的充电器，如一个5 kW充电器的退化成本最低，而一个40 kW充电器的退化成本最大。然而，如果我们看看聚合器的成本，它是不同的。聚合器的成本似乎会随着高功率的增加而降低，因为一个高功率的充电器可以在更低的能源价格时期提供更多的能量。然而，5 kW充电器是最适合整体的，因此与其他三个充电器相比，成本最低。

在第（5-2）节中，我们观察到，在能源需求不高的情况下，使用较低等级的充电器效果更好。因此，在这种情况下，对100个能源需求场景实施了一个可变的充电器分配，以帮助降低退化和聚合器成本。最后，我们将其与满足所有能源需求场景的40 kW充电器外壳进行了比较。聚合器的能源需求如图（5-6）所示。聚合器的需求是基于能源价格的。因此，能源是在能源价格较低的时期添加的。首先，从07：00到16：00，电动汽车不增加能量，这在驾驶轮廓（5-2）中给出。在其余的时间里，电动汽车就会被连接到电网上。在此期间，电动汽车试图在00：00、01：00：00、02：00和21：00时投入最大能量。这是因为，在那个时候，能源价格很低，而聚合器试图将成本最小化。然而，如果我们比较40 kW充电器和可变充电器，我们可以观察到40 kW充电器在价格较低的时候有更多的充电自由。因此，它可以尽可能低地降低聚合器的成本。 

 

在图（5-7）中，计算了40 kW充电器和可变充电器外壳的车队退化成本。40 kW充电器的机队退化率远远高于可变充电器的情况。这是因为在可变充电器外壳中分配的充电器是基于能量需求的。例如，如果能源需求大于40kWh，小于128kWh，16 kW可以满足需求。结果还表明，低差充电器将降低降解成本。因此，可变充电器外壳是两者中更合适的情况，因为它显著降低了机队的退化成本。

 

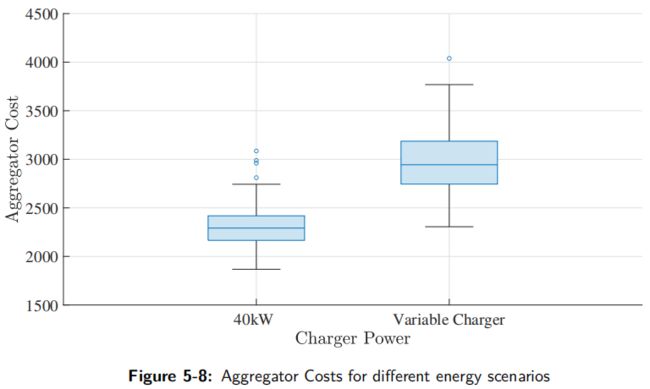
整个车队的聚合成本见（5-8）。与退化成本不同，可变充电器外壳的聚合器成本大于40 kW充电器。如图（5-6）所示，可变充电器的聚合器需求大于40 kW充电器外壳。因此，它会导致更高的成本。最后，舰队的总成本如图（5-9）所示。总成本是退化成本和聚合器成本的总和。现在，尽管40 kW的聚合器成本比可变充电器更好，但所产生的退化成本却相当高。因此，可变充电器的总成本小于40 kW充电器。

从上述仿真结果可以看出，根据能源需求使用不同功率水平的充电器比使用相同功率水平的充电器更好。所产生的总成本大大降低了。因此，在这种情况下，当电动汽车只连接到电网一次时，可变功率充电方法更适合。

5.matlab代码

完整代码可以从下面的链接获取：

GitHub - adithyanarsi97/Optimal-fleet-Charging-for-Electric-Vehicle-Fleets-using-ADMM