二、搜索与图论6:Dijkstra 模板题+算法模板(Dijkstra求最短路 I, Dijkstra求最短路 II,1003 Emergency)
文章目录
- 算法模板
-
- Dijkstra题目代码模板
-
- 朴素dijkstra算法
- 堆优化版dijkstra
- 树与图的存储
-
- (1) 邻接矩阵:
- (2) 邻接表:
- 关于e[],ne[],h[]的理解
- 关于堆的原理与操作
- 模板题
-
- Dijkstra求最短路 I
-
- 原题链接
- 题目
- 思路
- 题解
- Dijkstra求最短路 II
-
- 原题链接
- 题目
- 思路
- 题解
- 1003 Emergency
-
- 原题链接
- 题目
- 思路
- 题解
算法模板
Dijkstra题目代码模板
朴素dijkstra算法
对应模板题:Dijkstra求最短路 I
时间复杂是 O(n^2+m):n 表示点数,m 表示边数



int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
堆优化版dijkstra
对应模板题:Dijkstra求最短路 II
时间复杂度 O(mlogn):n 表示点数,m 表示边数



typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
树与图的存储
树是一种特殊的图,与图的存储方式相同。
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
(1) 邻接矩阵:
g[a][b] 存储边a->b
(2) 邻接表:
https://www.acwing.com/video/21/
(1:20:00左右)
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;
// 添加一条边a->b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int main(){
...
// 初始化
idx = 0;
memset(h, -1, sizeof h);
...
}
有权重时模板:
int h[N],w[N],e[N],ne[N],idx;
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
关于e[],ne[],h[]的理解
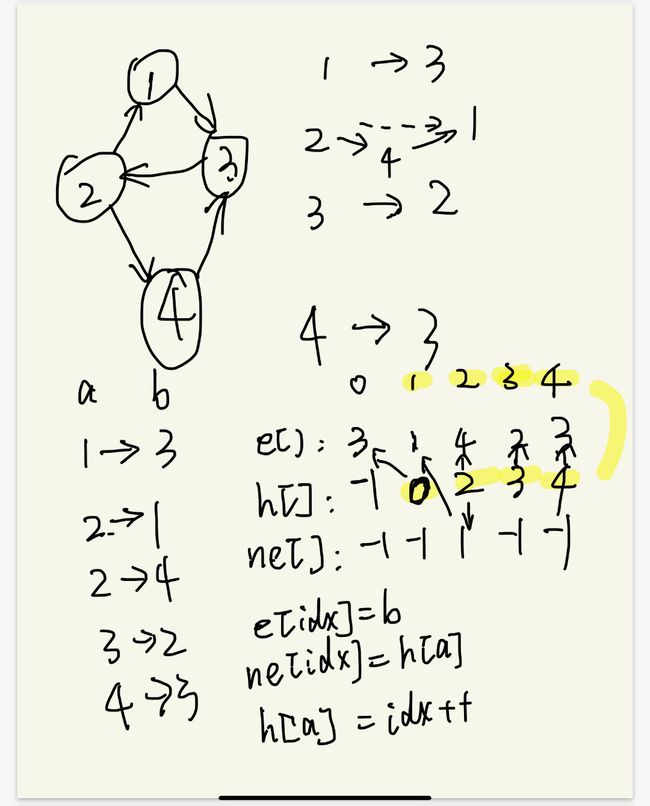
h[N] : 表示 第 i 个节点的 第一条边的 idx
ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
e[M] : 表示 第idx 条边的 终点
N : 节点数量
M:边的数量
i : 节点的下标索引
idx : 边的下标索引
变量初始化定义:
int h[N], e[M], ne[M], idx;
当我们加入一条边的时候:
void add(int a,int b){
e[idx] = b; // 记录 加入的边 的终点节点
ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标,ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面,其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面;目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边,完成把最新的一条边插入到 链表头的操作;
h[a] = idx++; // a节点开头的第一条边置为当前边,idx移动到下一条边
}
要注意的是邻接表插入新节点时使用的是“头插”,如图中节点2:当插入2 1时此时为2—>1, 而后插入2 4后,此时为 2—> 4 —> 1.

关于堆的原理与操作
二、数据结构10:堆 模板题+算法模板(堆排序,模拟堆)
模板题
Dijkstra求最短路 I
原题链接
https://www.acwing.com/problem/content/851/
题目
给定一个 n
个点 m
条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1
号点到 n
号点的最短距离,如果无法从 1
号点走到 n
号点,则输出 −1
。
输入格式
第一行包含整数 n
和 m
。
接下来 m
行每行包含三个整数 x,y,z
,表示存在一条从点 x
到点 y
的有向边,边长为 z
。
输出格式
输出一个整数,表示 1
号点到 n
号点的最短距离。
如果路径不存在,则输出 −1
。
数据范围
1≤n≤500
,
1≤m≤105
,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路
题解
#include Dijkstra求最短路 II
原题链接
https://www.acwing.com/problem/content/852/
题目
给定一个 n
个点 m
条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1
号点到 n
号点的最短距离,如果无法从 1
号点走到 n
号点,则输出 −1
。
输入格式
第一行包含整数 n
和 m
。
接下来 m
行每行包含三个整数 x,y,z
,表示存在一条从点 x
到点 y
的有向边,边长为 z
。
输出格式
输出一个整数,表示 1
号点到 n
号点的最短距离。
如果路径不存在,则输出 −1
。
数据范围
1≤n,m≤1.5×105
,
图中涉及边长均不小于 0
,且不超过 10000
。
数据保证:如果最短路存在,则最短路的长度不超过 109
。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路
使用堆优化,选择用stl中的priority_queue进行操作
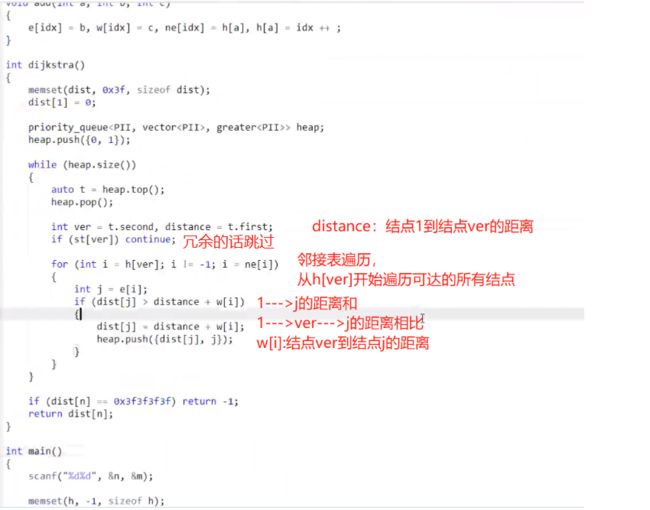
关于st[N]数组 处理冗余部分
https://www.acwing.com/solution/content/167860/
题解
#include 1003 Emergency
原题链接
原题链接
题目
题目大意:n个城市m条路,每个城市有救援小组,所有的边的边权已知。给定起点和终点,求从起点到终点的最短路径条数以及最短路径上的救援小组数目之和。如果有多条就输出点权(城市救援小组数目)最大的那个
思路
用一遍Dijkstra算法,救援小组个数相当于点权,用Dijkstra求边权最小的最短路径的条数,以及这些最短路径中点权最大的值
dis[i]表示从出发点到i结点最短路径的路径长度,
num[i]表示从出发点到i结点最短路径的条数,
w[i]表示从出发点到i点救援队的数目之和
当判定dis[u] + e[u][v] < dis[v]的时候,
不仅仅要更新dis[v],还要更新num[v] = num[u], w[v] = weight[v] + w[u];
如果dis[u] + e[u][v] == dis[v],还要更新num[v] += num[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u];
题解
基于上述朴素版dijkstra进行改进,
#include
// w[j]+=weight[t];
}
else if(dist[j]==dist[t]+g[t][j]){ //如果dis[u] + e[u][v] == dis[v],还要更新num[v] += num[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u];
num[j] = num[t]+num[j];
if(w[t]+weight[j] > w[j]){
w[j] = w[t] + weight[j];
}
}
}
}
// return w[c2];
}
int main(){
cin>>n>>m>>c1>>c2;
for(int i=0;i<n;i++){
int t;
cin>>t;
weight[i] = t;
}
memset(g,0x3f,sizeof g); // 赋值无穷大
for(int i=0;i<m;i++){
int x,y,z;
cin>>x>>y>>z;
g[x][y] = g[y][x] = z; // 无向图!所以存双向信息
}
dij();
cout<<num[c2]<<" "<<w[c2];
}
参考链接:1003. Emergency (25)-PAT甲级真题(Dijkstra算法)


