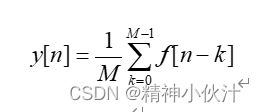Matlab实现基于滑动平均的信号去噪
一、基本信号处理
1. 信号、噪声功率计算
2. 信噪比
3. 信号的频域分析
二、噪声的仿真与去除
滑动平均去噪是工程上普遍应用的去噪方法,设受噪声干扰的信号为f[n]=s[n]+d[n],其中为有用信号为s(n)=-2n*n+4n,d[n]为噪声。已知M点滑动平均系统的输入输出关系为
编程实现用M点滑动平均系统对受噪声干扰的信号的去噪。
本仿真的关键是描述M点滑动平均系统,以6点滑动平均为例:
系统可描述为:filter([1/6 1/6 1/6], [1])
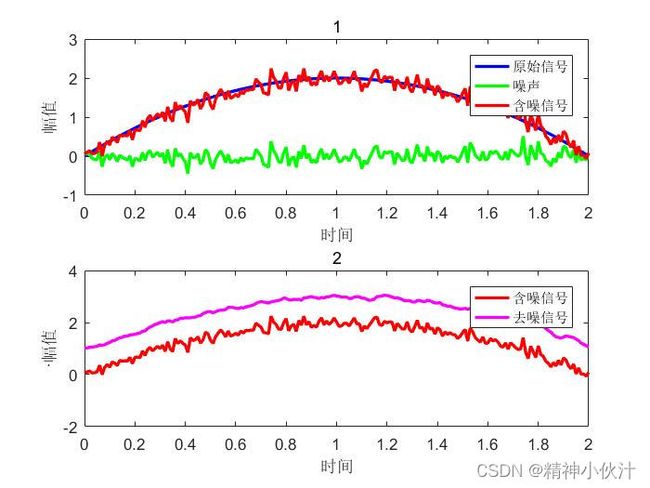
运行结果如图2-7所示,由去噪分析结果可知,M点滑动平均去噪法用于计算的点数越多,去噪效果越好,但是产生的时移也越大,因此在工程去噪中应合理选择去噪的参数。
程序关键代码和波形显示结果如下
clear; clc; close all;
n = 0:0.01:2;
N = length(n);
snr = 20;
sn =-2.*n.^2+4.*n ;
Ps = sum(sn.^2); %计算信号的功率Ps
Pn = Ps / (10^(snr/10)); %计算噪声的功率Pn
un = sqrt(Pn/N); %计算噪声的标准差un
noise = un * randn(1, 201); %生成长度为200的高斯分布噪声
snn = sn + noise; %含噪信号
M = 6; % 滑动6均系统的窗口大小
wu = zeros(1, N); % 存储去噪后的信号
for i=1:N
if i<=M
% qu(i)=0;
wu(i) = sum(snn(1:i))/M;
%wu(i)=0;
else
wu(i)=sum(snn(i-M+1:i))/M;
end
end
subplot(2,1,1);
plot(n, sn, 'b', 'LineWidth', 2);
hold on;
plot(n,noise, 'g', 'LineWidth', 2);
hold on;
plot(n, snn, 'r', 'LineWidth', 2);
hold on;
legend('原始信号', '噪声', '含噪信号');
title('1');xlabel('时间');ylabel('幅值');
subplot(2,1,2);
plot(n, snn, 'r', 'LineWidth', 2);
hold on;
plot(n, wu+1, 'm', 'LineWidth', 2);
hold on;
legend( '含噪信号', '去噪信号');
title('2');xlabel('时间');ylabel('·幅值');
1、运行程序。上图生成原信号,噪声信号,含噪信号的时域波形,并进行加注标题、颜色变换,并把每个颜色对应的是什么信号标注出来;下图是去噪信号和含噪信号的对比图,粉色为去噪信号,红色为含噪信号(为了便于比较去噪信号和含噪信号,将“去噪信号”向上平移一个单位)。
2、算法分析:实现过程简单,目标明确,由于滤波方式为标准差分方程,直接采用filter函数。多次取值得出结论:M点滑动平均去噪法用于计算的点数越多,去噪效果越好,但是产生的时移也越大。