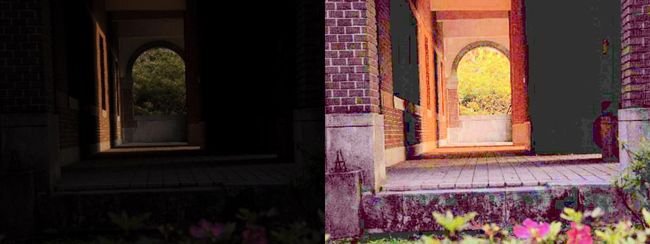一文搞懂直方图均衡

直方图均衡

定义

根据维基百科上的定义, 直方图均衡(Histogram Equalization)是图像处理领域中利用直方图对对比度进行调整的方法.

顾名思义, 直方图均衡是将直方图的分布(概率密度)调整为均匀分布.

为什么要做直方图均衡

根据信息论, 信息的熵越大, 包含的信息也就越多, 熵的计算公式如下:

$$H=-\sum _{i=0}^{n}p(x_i)lo{g}_2(p(x_i))\text{\hspace{1em}(1)}$$

只有当 $p(x_i)$​ 均匀分布时, 熵的值最大. 对应到图像上, 当图像直方图均匀分布时, 图像对比度最大. 如下图所示:

蓝色为原始图像直方图, 绿色为均衡后直方图, 对应的处理后的图像为:

可以看到, 直方图均衡处理后, 图像变得更加清晰了.

怎么做直方图均衡

知道了为什么, 就要知道怎么做. 一般直方图均值有以下几个步骤:

1. 统计图像的直方图, 归一化到[0,1]

$$p_r(r_k)=\frac{n_k}{H\ast W},k=0,1,2,\cdot ,L-1\text{\hspace{1em}(2)}$$

2. 计算映射函数

$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)\text{\hspace{1em}(3)}$$

式中, $H$, $W$ 分别为图像的高和宽, $n_k$ 表示灰度值为 $r_k$ 的像素的个数, $s_k$ 为变换后的灰度值, $T(r_k)$ 为映射函数, 计算过程使用了累计直方图.

3. 利用得到的映射函数, 对图像进行处理
4. 对于RGB图像, 可以转到HSV空间, 对V通道进行均衡后, 转回RGB空间, 如下图所示结果:

为什么可以这么做

知道怎么做了, 就要知道为什么可以这么做. 这里解释下为啥可以这么做, 即公式(3)是怎么得到的.

设原始直方图分为为
$$p_r(r_k)$$

均衡化后的直方图分布为
$$p_s(s_k)=\frac{1}{L-1}\text{\hspace{1em}(4)}$$

映射函数为
$$s_k=T(r_k)$$

这里映射函数必须为单调递增函数, 满足:

$${\int }_0^{s_k}{p}_s(s)ds={\int }_0^{r_k}{p}_r(r)dr\text{\hspace{1em}(5)}$$

即对应区域间内像素点的总数是一样的, 如下图红色区域所示:

将公式(4)代入公式(5), 则有:

$$\frac{s_k}{L-1}={\int }_0^{r_k}{p}_r(r)dr$$

因而, 可以得到:

$$s_k=(L-1){\int }_0^{r_k}{p}_r(r)dr\text{\hspace{1em}(6)}$$

对应的离散形式为公式(3).

存在问题

1. 如果映射函数为公式(6), 为连续形式, 这种映射是可逆的, 但更改为离散形式, 公式(3)后, 变成了不可逆的.
2. 映射变换会丢失信息, 对出现比例很少的灰度进行合并, 从而会丢失部分细节.
3. 对于占比例较多的灰度, 则会将其拉伸, 而导致其占据了更多的灰度, 压缩了其他灰度.

改进

直方图均衡过度的强调了灰度个数的重要性, 对数量多的灰度过度的进行了增强, 而图像中, 比例比不是很多的灰度往往更重要, 因而改进的方向就是减少数量多的灰度的影响, 我这里想到的有 3 种方法:

1. 对直方图开根号, 减少数量多灰度的影响;
2. 对直方图进行截断, 超过部分数量直接去除, 从而减小数量多灰度的影响;
3. 在第2种方法的基础上, 将超出部分均匀的加到直方图的每个bin上(该想法来源于CLAHE);

这3种方法的映射关系曲线如下所示:

从图中可以看到, 原始的直方图均衡后图像最亮, 如下所示为几种方法的结果对比, 依次为原图, 原始直方图, 改进0, 改进1, 改进2:

可以看到, 直方图可以改善图像整体的质量, 但对于某些局部图像, 则由于直方图的性质导致过亮或者过暗.

小结

这里总结下直方图均衡化的优缺点:

1. 直方图均衡化算法简单, 速度快;
2. 可以改善图像整体质量;
3. 但对于图像局部质量改善效果不是很好;

参考

1. https://zhuanlan.zhihu.com/p/44918476
2. https://zhuanlan.zhihu.com/p/78017679
3. https://zhuanlan.zhihu.com/p/37168516
4. https://zh.wikipedia.org/wiki/%E7%9B%B4%E6%96%B9%E5%9B%BE%E5%9D%87%E8%A1%A1%E5%8C%96
5. https://blog.csdn.net/yanhe156/article/details/83083659