【动态规划算法】-回文串问题题型（34-40题）
作者：小树苗渴望变成参天大树
作者宣言：认真写好每一篇博客
作者gitee:gitee✨
作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法
如 果 你 喜 欢 作 者 的 文 章 ，就 给 作 者 点 点 关 注 吧！
文章目录
- 前言
- 第三十五题：[647. 回文子串](https://leetcode.cn/problems/palindromic-substrings/)
- 第三十六题：[5. 最长回文子串](https://leetcode.cn/problems/longest-palindromic-substring/)
- 第三十七题：[1745. 分割回文串 IV](https://leetcode.cn/problems/palindrome-partitioning-iv/)
- 第三十八题：[132. 分割回文串 II](https://leetcode.cn/problems/palindrome-partitioning-ii/)
- 第三十九题：[516. 最长回文子序列](https://leetcode.cn/problems/longest-palindromic-subsequence/)
- 第四十题：[1312. 让字符串成为回文串的最少插入次数](https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/)
前言
今天博主来讲解动态规划的另一个题型就是回文串问题，这个系列的问题，套路差不多，首先大家要了解什么是回文串，就是在原串中选出连续的一个子串，判断是不是回文的即可，接下来我们将会一题题的给大家进行讲解，话不多说，我们开始进入正文
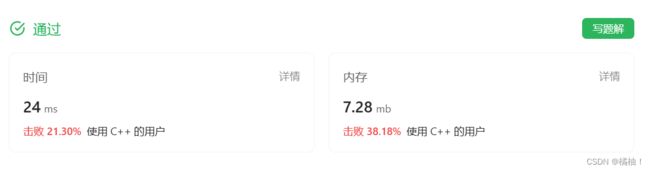
第三十五题：647. 回文子串
题目解析：
动态规划算法：
1. 状态表示：经验+题目要求
做这个系列的问题我们就是将子串是否为回文的结果放到dp表里面，因为你要插进来的字符是否和前面构成回文，首先保证前面的子串是回文才行，所以我们的dp表，需要一个二维的，表示回文子串的起始和结尾
dp[i][j]表示：以i,j位置为结尾的子串是否为回文子串，(i<=j)
2. 状态转移方程：
3. 初始化：保证数组不越界
我们j是大于等于i的，但是会越界的情况已经单独拿出来分析了，所以不用初始化
4. 填表顺序：
所以我们要从上往下进行填表
5. 返回值:
返回为真的个数就可以了
代码实现：
class Solution {
public:
int countSubstrings(string s) {
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));
int count=0;
for(int i=n-1;i>=0;i--)
{
for(int j=i;j<n;j++)
{
if(s[i]==s[j])
{
if(i==j||i+1==j)
dp[i][j]=true;
else
dp[i][j]=dp[i+1][j-1];
}
if(dp[i][j]==true) count++;
}
}
return count;
}
};
运行结果：
这一题可以说是为后面的题目做铺垫，相当于一个引子
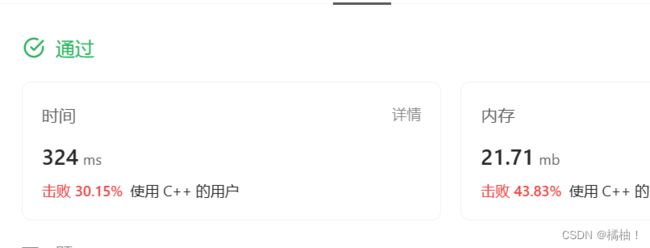
第三十六题：5. 最长回文子串
题目解析：
此题就是找到最长回文子串，做法和上一题一模一样，先用dp表存放是否构成回文串，有起始位置和结束位置就可以算出来长度。
动态规划算法：
1. 状态表示：经验+题目要求
dp[i][j]表示：以i,j位置为结尾的子串是否为回文子串，(i<=j)
2. 状态转移方程：
每次填完dp表的时候，就计算一个长度，i表示起始位置，j表示结束位置，长度为j-i+1,
3. 初始化：保证数组不越界
我们j是大于等于i的，但是会越界的情况已经单独拿出来分析了，所以不用初始化
4. 填表顺序：
所以我们要从上往下进行填表
5. 返回值:
将长度和起始位置算出来，通过substr来获取子串返回即可
代码实现：
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));
int len=1,start=0;
for(int i=n-1;i>=0;i--)
{
for(int j=i;j<n;j++)
{
if(s[i]==s[j])
{
if(i==j||i+1==j)
dp[i][j]=true;
else
dp[i][j]=dp[i+1][j-1];
}
if(dp[i][j]&&len<j-i+1)//选出最长的回文子串
{
len=j-i+1,start=i;
}
}
}
return s.substr(start,len);
}
};
运行结果：
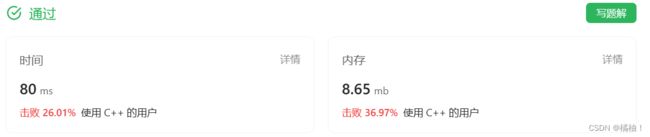
第三十七题：1745. 分割回文串 IV
题目解析：
这个题目还是非常的好理解的，因为有固定的数，分成三个回文子串。
先将子串是否为回文子串放到dp表里面，然后再枚举dp表就行了。
这题我就不详细讲解了，直接上代码了
代码实现：
class Solution {
public:
bool checkPartitioning(string s) {
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));
int count=0;
for(int i=n-1;i>=0;i--)//将子串是否是文回放到dp表里面
{
for(int j=i;j<n;j++)
{
if(s[i]==s[j])
{
if(i==j||i+1==j)
dp[i][j]=true;
else
dp[i][j]=dp[i+1][j-1];
}
}
}
for(int i=1;i<n-1;i++)//第一个至少要留出来一个位置
{
for(int j=i;j<n-1;j++)//最后一个也要留出来一个位置
{
if(dp[i][j]&&dp[0][i-1]&&dp[j+1][n-1])
return true;
}
}
return false;
}
};
运行结果：
第三十八题：132. 分割回文串 II
题目解析：
动态规划算法：
1. 状态表示：经验+题目要求
我们以某一个位置来考虑问题：
dp[i]表示：从0开始到以i位置为结尾的子串中将子串分割成每个部分都是回文子串的最少的切割次数
2. 状态转移方程：
这题和单词拆分的思想有点像，再[0,i]区间中选择一个j，此时j位置就是最后一刀切割的地方，前面切割的次数，加上最后一刀就是总次数
3. 初始化：保证数组不越界
j-1是不会越界的，j>0的。
因为要保证第一次求最小值的时候不能干扰到选择dp[j-1]+1，所以不初始化，就为01，那么最小值一直都是0,所以干脆就初始化为最大值。
4. 填表顺序：
从左往右
5. 返回值:
返回dp[n-1];
代码实现：
class Solution {
public:
int minCut(string s) {
int n=s.size();
vector<vector<bool>> isPal(n,vector<bool>(n));
int count=0;
for(int i=n-1;i>=0;i--)//将子串是否是文回放到dp表里面
{
for(int j=i;j<n;j++)
{
if(s[i]==s[j])
{
if(i==j||i+1==j)
isPal[i][j]=true;
else
isPal[i][j]=isPal[i+1][j-1];
}
}
}
//创建dp表+初始化
vector<int> dp(n,INT_MAX);
for(int i=0;i<n;i++)
{
if(isPal[0][i])
{
dp[i]=0;
}
else
{
for(int j=1;j<=i;j++)
if(isPal[j][i])
dp[i]=min(dp[j-1]+1,dp[i]);
}
}
//返回值
return dp[n-1];
}
};
运行结果：
第三十九题：516. 最长回文子序列
题目解析：
动态规划算法：
1. 状态表示：经验+题目要求
dp[i]表示：以i位置元素为结尾的子序列中最长的回文子序列的长度
上面的状态表示不行，我们要重新定义状态表示，定义两个位置
dp[i][j]表示：s字符串里面【i，j】子区间内的所有子序列中最长回文子序列的长度
2. 状态转移方程：
3. 初始化：保证数组不越界
我们看到会使用到使用到j-1或者i+1位置的值
4. 填表顺序：
我们会使用到
dp[i+1][j]正下方的值
dp[i][j-1]左边的值
dp[i+1][j-1]左下方的值
从下往上，从左往右
5. 返回值:
返回整个字符串区间dp[0][n-1]
代码实现：
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n=s.size();
//创建dp表
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;i--)//从下往上
{
dp[i][i]=1;//此情况肯定是相等的
for(int j=i+1;j<n;j++)//从左往右
{
if(s[i]==s[j])dp[i][j]=dp[i+1][j-1]+2; //放在一起考虑了
else dp[i][j]=max(dp[i][j-1],dp[i+1][j]);//不相等的时候
}
}
//返回值
return dp[0][n-1];
}
};
运行结果：
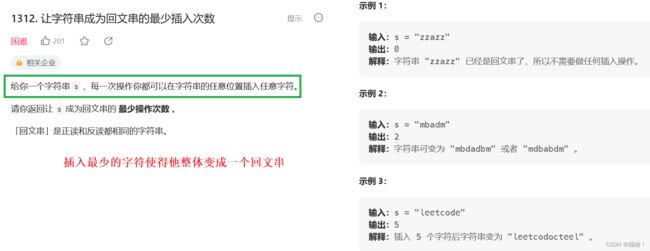
第四十题：1312. 让字符串成为回文串的最少插入次数
题目解析：
这题还是按照上一题的分析方式一样，选择一个区间去分析。
动态规划算法：
1. 状态表示：经验+题目要求
dp[i][j]表示：s字符串以[i,j]区间内想要变成回文串要插入的最少次数
2. 状态转移方程：
3. 初始化：保证数组不越界
根据上题的分析无需初始化
4. 填表顺序：
从下往上，从左往右
5. 返回值:
dp[0][n-1];
代码实现：
class Solution {
public:
int minInsertions(string s) {
int n=s.size();
//创建dp表
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;i--)//从下往上
for(int j=i+1;j<n;j++)//从左往右，从i+1位置，因为i==j的情况为0不需要考虑
if(s[i]==s[j])dp[i][j]=dp[i+1][j-1];
else dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;
//返回值
return dp[0][n-1];
}
};
运行结果：
到这里我们的回文串问题就讲解完毕了，这类题型之间的练习都挺大了，上一题的经验可以大量的运用到下一题上，这给我们的学习也带来了很大的帮助，但凡不是一题题做过来的，那么后面的每一题都很难想到，所以我们要善于总结，这样下次单独碰到一题就不会没有头绪，好了，我们今天的题目就先讲解到这里了，我们下篇介绍关于两个数组的dp问题。