第十三届蓝桥杯：A组Java前三题试题A:裁纸刀+试题B:寻找整数+试题C：求和

EF题：(170条消息) 第十三届蓝桥杯JavaB组中三题：试题D：最少刷题数+试题E：求阶乘_我在赶来的路上武理的博客-CSDN博客

试题A:裁纸刀

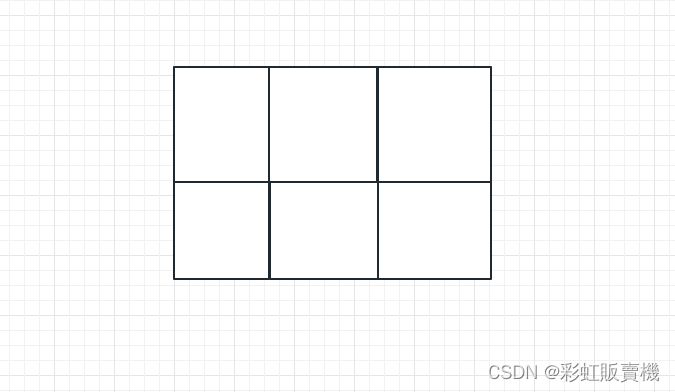
 就是简单数学问题：n行m列

总裁剪次数等于num = 4 + (n-1) + n(m-1)，直接sout输出答案

System.out.println(4+19+20*21);

试题B:寻找整数
 

从2开始，一个数num满足num%2==1,则以后的每一次叠加都要是2的倍数，才能满足新的num%2还等于1

在每次叠加2的基础上，再找到了一个满足num%3==2的数，则以后的每一次叠加都要是2*3的倍数，才能满足新的num%2还等于1 以及 新的num%3还等于2..........

[注]要先找两个数最小公约数 , 再找出最小公倍数  ，通过公倍数找出上面描述的数字；加上公倍数，就不会让之前求模运算白费！

public class Main {
    public static void main(String[] args) {
        long[] a = {0, 0,
                1, 2, 1, 4, 5, 4, 1, 2, 9, 0, 5, 10,
                11, 14, 9, 0, 11, 18, 9, 11, 11, 15, 17, 9,
                23, 20, 25, 16, 29, 27, 25, 11, 17, 4, 29, 22,
                37, 23, 9, 1, 11, 11, 33, 29, 15, 5, 41, 46};
        long ans=1;
        long c=1;

        for (int i = 2; i < a.length-1; i++) {
          //先找出一个一个的除数之间的最小公倍数
          // i = 2,3,4,5时
          c = gongbeishu(c,i);    //除数2,3 -> 6  ,6,4->12, 12,5->60

          //i = 2,3,4,5时，如果，ans%(i+1)不等于表中取模的值，那么就加公倍数，直到加到取模等于表中取模值
          //我们通过加最小公倍数，这样 加上的值的取模运算会等于0，前面的取模就不会改变
          while( ans%(i+1) != a[i+1]){
            ans = ans + c;        //1 + 2 + 2 = 5  
          }
          
        }
        System.out.println(ans);
    }

    //最小公倍数
    public static long gongbeishu(long a,long b){
      //先求最小公因数，
      long c = gongyinshu(a,b);
      return (a/c) * (b/c) * c;
    }

    //求最小公因数
    public static long gongyinshu(long a,long b){
      if(b == 0) return a;
      return gongyinshu(b,a%b);
    }
}

试题C：求和

//假如有5个数：a0,a1,a2,a3,a4
//求解：
//      sum0 = a0 + a1 + a2 + a3 + a4
//      用乘法分配律进行分组求和
//      sum1 = ( a1 + a2 + a3 + a4 ) * a0 = (sum0 - a0                ) * a0
//      sum2 = (      a2 + a3 + a4 ) * a1 = (sum0 - a0 - a1           ) * a1
//      sum3 = (           a3 + a4 ) * a2 = (sum0 - a0 - a1 - a2      ) * a2
//      sum4 = (                a4 ) * a3 = (sum0 - a0 - a1 - a2 - a3 ) * a3

public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        long[] arrs = new long[n];
        long sum = 0;

        //记录数组，并且对数组求和
        for(int i=0;i