因为前几天作死立了一个flag说要把NOIP近十年的题目做一做,并写一个题目归类+题解摘要出来,所以这几天就好好的(然而还是颓废了好久)写了一些这些往年的NOIP题目。
这篇博客有什么:
近十年NOIP题目归类+简要题解+AC程序+相似题目(双倍经验之类的)
备注:
但是因为本蒟蒻实在太蒻了,好多题目只会打暴力拿部分分数,想不到正解,所以在写题的时候参考了一些博客和题解,所以自然这篇博客也借用了一部分dalao的思路和想法(但是最后还是本蒟蒻独立完成的就是了),在此对各位提供帮助的dalao表示深深的感谢。
博客里面按照分类加入了NOIP题目链接以及凭借本蒟蒻做题看到的一些相似题目链接,题目链接来源于洛谷。
应该是更新完了。。。如果有哪个题忘了写,还请dalao们在评论区指出。
搜索,模拟:
1、2008T2 火柴棒等式(打表)(搜索)
就是简单的搜索(貌似连剪枝都不需要),但是也可以打表(打表大法好!!)在此就不放题解了。
2、2009T1 潜伏者(字符串)(模拟)
字符串模拟水题,不放题解了。
3、2009T4 靶形数独(搜索)
题解什么的已经以专题的形式写过了,在这里放链接好了: 数独问题
4、2010T1 机器翻译(搜索)(队列)
还是水题,就不放题解了。
5、2010T4 引水入城(搜索)(动态规划)
这道题有两问,求没有被覆盖到的沙漠地带可以用搜索来看下面有没有被完全覆盖到,直接dfs+判断即可。但是求需要的蓄水站需要我们求出来不可能被覆盖的区域个数。
本来想的是用贪心求解,但是因为覆盖区间有重复,所以有点麻烦。
因为只有最后一行需要水源覆盖,所以我们需要记录每个点能够到达最后一行的区间。这个操作可以用dfs来实现。但是考虑到dfs可能时间复杂度有点高,所以我们采取记忆化搜索(开数组记录能够到达最左边和最右边的位置)。
为了解答第二问,我们需要做区间覆盖,核心代码如下:
while (left<=m){
int maxr=0;
for (int i=1;i<=m;i++)
if (l[1][i]<=left)
maxr=max(maxr,r[1][i]);
//寻找左端点在当前点之前并且右端点最靠右的区间
cnt++;
//找到一个区间(一个蓄水站可以覆盖的区间)答案加一
left=maxr+1;
//更新当前点
}标程
5、2011Day1T1 铺地毯(模拟)(离散化)
这是水题,就是倒着枚举。但是和它思想类似的还有HAOI2014贴海报
6、2011Day1T3 Mayan的游戏(搜索)(模拟)
这个题目可真恶心,怎么这么考验代码能力啊
写这个题一定要明白将函数分开写的好处!要不然写一会儿就云里雾里,不知道自己在干什么了。
介绍函数:
cut_off:
搜索有没有可以消去的相连方块,如果有就将可以消去的方块消去并且返回true,没有就返回false。
这里需要注意的是因为存在诸如图5情况,所以遍历到有连着三个或者以上的方块一定不要立刻消去,而应该采取打标记的方法,之后再消去。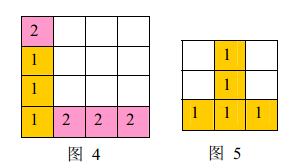
这里我们采取从选定格子向四周拓展的方法,暴力地遍历判断是否有格子需要消去,并将其打上标记。(暴力代码写的真长,我太蒻了)
fall:
这个是消去格子之后使得悬空的格子降落的函数
clear_up:
这个是判断是否符合游戏结束标准的函数(也就是遍历一遍,看看是不是都空了)
move:
执行移动的函数。(在这里需要注意的是有可能移动之后会造成再次消去的情况,所以用while()来确保进行一系列操作后所以可以消去的情况都已经被执行过了)
search:
这个是核心啊。(最恶心的搜索)
题目要求的是按照字典序输出,所以我们从最左边开始搜索,先往右边走,在往左边走。
有一个小小的剪枝,就是显然如果两个格子颜色一样,就不需要交换了。
但是这个貌似会T,看了题解之后才知道如果左边有格子就不需要再往左边搜索了,因为我们是从左边搜索过来的,那个时候就已经搜索和右边格子交换的情况了。
当然我们需要一个辅助数组来记录每一步的状态ans,在回溯的时候使用。(这里使用\(ans[i][j]\)m,其中i表示步数,j(j\(\in{}\)[1,3])分别表示需要输出的x,y,移动方向)
标程
7、2012Day1T1 Vigenère 密码(模拟)(字符串)(map)
开map是水题,就是写起来比较麻烦(比如蒟蒻我,一个一个插入的,累死了)
8、2013Day2T1 积木大赛(模拟)(贪心)
水题。就是从左到右扫一遍,不到高度的就补,到了高度就continue就可以了。
(值得吐槽的是这个是我当初高一加入我们学校机器人社团编程组的面试第三题,我当时高高兴兴地以为在社团编程也是竞赛之类的东西.......然后发现完全不一样好不好!所以说虽然很简单,但是为什么机器人编程组要考一道NOIP竞赛贪心题啊qwq(偷偷吐槽primy他应该不会知道吧))
9、2013Day2T3 华容道(搜索)(图论)
关键是记录状态的转移和建图操作;
题解:https://www.cnblogs.com/fengxunling/p/9773648.html
10、2014Day1T1 生活大爆炸版石头剪子布(模拟)(字符串)
水题。
11、2014Day2T1 无线网络发射器选址(模拟)
水题。
12、2015Day1T1 神奇的幻方(模拟)
水题。
13、2015Day1T3 斗地主(搜索)(模拟)(贪心)
其实很水,就是细节有点多。。。注意不是纯搜索+剪枝,还要有贪心的。。。。
题解:https://www.cnblogs.com/fengxunling/p/9862768.html
14、2016Day1T1 玩具谜题(模拟)
一个稍微麻烦一点的模拟。
15、2016Day2T3 愤怒的小鸟(搜索)(状压DP)
虽然说有状压DP的做法。。。但是蒟蒻不会啊!要不然回来再补状压DP的做法好了qwq(咕咕咕)
这里介绍的是一种搜索的方法——
就是最简单的搜索啦~~(fake),爆搜肯定过不去啊,所以我们要考虑很多魔性剪枝。
我们构造一个搜索,用dfs(c,u,v)表示当前搜到第c只猪,已构造抛物线的数量为u,单独的猪的数量为v时的情况。
这道题做的时候参考了 我在学习 dalao的题解,他的题解超详细的说,如果不懂的话完全可以去参考戳我
注意我们计算有二次函数计算,所以涉及到了浮点小数,所以注意判断相等的操作的时候不要直接“==”!!
标程
16、2017Day1T2 时间复杂度(模拟)(栈)
就是一个大模拟,但是由于循环可以嵌套,所以我们考虑栈的数据结构。。。。为了方便,我们可以开两个栈,一个来存名字,一个来存时间复杂度。
然后我们可以开两个函数,一个判断是否有名字重复,一个判断时间复杂度是否符合条件。
然后就是各种特判啦考试的时候这种模拟题一定要多造几组数据争取hack掉自己的程序,要不然极其容易WA掉啊!(比如说我第一次交才36分呐)
注意输入没有输入完的话,一定不要输出答案然后continue或者break掉,这样会RE的!!
下面是我的代码(带了超详细的输出调试信息),自认为还是比较好理解+简洁的(fake)
标程
数学:
1、2008T1 笨小猴(素数判断)(排序)
素数判断+快速排序,就是很简单数学题,素数判断写最简单的那种就行。
2、2009T2 Hankson的趣味题(gcd,lcm)
这个题如果想跑暴力分数貌似还是蛮高的,但是正解需要一个结论:
对于两个正整数a,b,如果\(gcd(a,b)=k\),那么\(gcd(a/k,b/k)=1\)。
知道了这个结论之后,我们要尝试应用:
\(lcm(x,b0)=b1\)
\(gcd(x,b0)=\frac{x*b0}{lcm(x,b0)}=\frac{x*b0}{b1}\)
\(gcd(\frac{x*b1}{x*b0},\frac{b0*b1}{x*b0})=1\)
\(gcd(\frac{b1}{b0},\frac{b1}{x})=1\)
同理:
\(gcd(\frac{x}{a1},\frac{a0}{a1})=1\)
综合以上两个式子得到以下结论:
x是a1的整数倍而且也是b1的因子。
所以我们可以枚举b1的因子(而且只需要枚举到\(\sqrt{b1}\)就可以了,因为它是因子,所以后面的我们可以通过b1处以它来获得),然后判断是不是a1的整数倍就可以了。
然后注意一下如果不是\(\sqrt{b1}\)的话ans+=2,如果正好是的话只能增加一个答案。
标程
3、2011Day2T1 计算系数(杨辉三角)
就是很水的数论题,用到了数学必修三的知识杨辉三角。
那么就不放题解了qwq。
4、2012Day1T2 国王游戏(数学)(高精)(排序)
通过数学推论我们可以知道要把左右手乘积按照从大到小排序才是最优解。
然后要高精度乘法,高精度除以低精度。
这里的高精度可以压位。
5、2012Day2T1 同余方程(拓展欧几里得)
ecgcd模板题。
6、2013Day1T2 火柴排队(排序不等式)(逆序对)(离散化)
做这个题需要知道排序不等式相关知识:正序和>=乱序和>=逆序和,
除此之外还要知道:如果将原本乱的数组按升序排序,并且每次只能交换一对数字的话,需要的次数是原序列逆序对的数量。
所以我们可以采用归并排序或者树状数组求逆序对(反正我是不会树状数组求逆序对)
不会求逆序对的来打模板---->模板
但是需要注意的是,这个题需要离散化!!
由于在离散化这里跪了,所以蒟蒻我只好取翻题解(哦,对了,顺便感谢BLUESKY007大佬的解释十分优秀地打好了辅助),题解里 ZJYelizaveta大佬是这么说的:
“这道题目的精华在于对于新建序列!
假设我们现在有离散化后的序列$ a={4,3,1,2}\(,\)b={1,3,2,4}$。
我们令 q[a[i]]=b[i],相当于以 a[i]为关键字对序列 b[i] 排序。
若序列 aaa 与序列 bbb 相等,那么此时 q[a[i]]应该等于 a[i] 的,也就是 q[i]=iq[i] = iq[i]=i。
那么也就是说如果我们想让序列 a 与序列 b 相等,那么我们需要让 q升序排列。
问题就变为,将原本乱的 q 序列升序排列的最少交换次数。”
标程
2014Day2T3 解方程(秦九韶算法)(读入优化大数取模)
qwq其实也没什么,就不放代码了qwq
2016Day2T1 组合数问题(杨辉三角)
其实只要看出来是杨辉三角,预处理出来一个杨辉三角的表,就是水题啦~~
分治
1、聪明的质检员(二分)(前缀和)(递推)
这个题目的题我真的是没有看懂(图片是什么意思qwq),在这里贴上别人的解释吧:
s是区间中w[i]>=W的个数,v是所有满足w[i]>=W的i的v[i]的和,那么这个贡献就是s*v。
那么就没有什么了,我们使用前缀和算出价值 sum[i]=sum[i-1]+v[i],数量 ge[i]=ge[i-1]+1(注意如果重量没有达到,不添加此次的价值和个数)
最后就是一个二分答案,查找和最佳答案。
标程
2、2012Day2T2 借教室(二分)(前缀和)
3、2013Day1T1 转圈游戏(快速幂)(数学)
快速幂水题
4、2015Day2T1 跳石头(二分)
水题,不说了。
顺便一提,双倍经验丢瓶盖
倍增
1、2012Day1T3 开车旅行(倍增)
题解:https://www.cnblogs.com/fengxunling/p/9755195.html
2、2013Day1T3 货车运输(LCA)(最大生成树)
在下面图论类别里有详解。
3、2012Day2T3 疫情控制(倍增)(树)(二分)
比较综合+码量很大的题qwq
题解:https://www.cnblogs.com/fengxunling/p/9759052.html
动态规划,递推:
imone dalao曾说,如何判断一道题是不是动态规划呢......可以参考数据范围,如果在三位数四位数左右就可以想动态规划了,而且状态设计同样则可以结合数据范围和变量,先想出开几维的数组,然后结合做题经验进行状态设计。(当然有时候可以运用滚动数组将一个维度滚动掉)据本蒟蒻的观点来讲,DP最重要的是状态设计和初始化......然后DP有很多种类啊,蒟蒻我题目见的也不多,好多题目也不会做。(对啦,在这里先orz机房DP大佬soul_M一波)
1、2008T3 传纸条(高维DP)
这是一个高维DP的题目,可以将将寻找矩形的一对对角顶点出发走到另一个对角顶点的不重复路线(两条)转换为从同一个顶点走到它的对角顶点的两条最短严格不相交路线。
注意由于终点的值是0,所以目标状态就是\(f[n][m-1][n-1][m]\)。(因为终点是边角啊,所以只有从终点上边或者左边过来qwq)
有一个叫做方格取数的题目和它很相似,可以水一波双倍经验-------->方格取数
(听说还可以用费用流做?反正我不会)
标程
2、2010T2 乌龟棋(高维DP)
因为只有四种前进方式,而且数据范围也不大,所以我们考虑开四位数组,每一维分别表示对应卡片运用了多少次。
注意初始化和起始位置为1。
这个代码加了读入优化(看起来有点长的样子)
标程
3、2011Day2T3 观光公交(递推)(贪心)
这个题目一看就是贪心,但是当年NOIP却有错误的贪心策略AC本题的情况(出题人估计是没有想周全),但是这并没有关系,因为落咕添加了hack数据!(毒瘤)
标程//标程里面有简要注释
4、2013Day2T2 花匠(动态规划)(贪心)
其实我是用贪心A掉的,所以说我也不会动态规划的做法。之所以放到这里是因为好多人都说它是动态规划,而且我也没有开贪心的标签qwq。
因为用贪心的方法做感觉这题比较水,就不放题解了qwq。
5、2014Day1T3 飞扬的小鸟(背包)(动态规划)
这个题目就是上升的话因为可以无限次点击,所以是完全背包;下降的话只有一次,所以是01背包。
注意问题模型的抽取与简化,注意处理飞到天花板(或者更高)的情况处理即可。
貌似有人说搜索也可以?反正我是不会啦
标程
6、2015Day2T2 子串(动态规划)(枚举)
先来设计状态:
设s[ i ][ j ][ k ]为A用到了 i ,B用到了 j ,已经用了 k 个子串, 并且一定用了当前字符(A[i])时的方案数。
设f[ i ][ j ][ k ]为A用到了 i ,B用到了 j ,已经用了 k 个子串, 无论用不用当前字符(A[i])时的方案数总和。
注意直接开数组是开不下的,所以要用滚动数组将其第一维滚动掉。
核心代码:
for(int i=1;i<=n;i++)
{
ans[v][0][0]=1;
for(int j=1;j<=m;j++)
{
for(int p=1;p<=k;p++)
{
if(s1[i]==s2[j])
sum[v][j][p]=(ans[u][j-1][p-1]+sum[u][j-1][p])%mod;
else sum[v][j][p]=0;
ans[v][j][p]=(ans[u][j][p]+sum[v][j][p])%mod;
}
}
int cur=u;
u=v;
v=cur;
}7、2016Day1T3 换教室(期望DP)
我们定义dp[i][j][0/1]来表示当前为第i个阶段,连同这一次已经用了j次换教室的机会,当前这次换(1)不换(0)的最小期望路程总和。
预先用floyd处理出教室之间的距离,然后然后状态转移的时候注意概率的问题(使用乘法分配律)
转换方式是这样的:
for(int i=2;i<=n;i++){
double add1=f[c[i-1]][c[i]];
for(int j=0;j<=min(m,i);j++)
{
dp[i][j][0]=min(dp[i-1][j][0]+add1,dp[i-1][j][1]+f[d[i-1]][c[i]]*p[i-1]+f[c[i-1]][c[i]]*(1-p[i-1]));
if(j!=0)
dp[i][j][1]=min(dp[i-1][j-1][0]+f[c[i-1]][d[i]]*p[i]+f[c[i-1]][c[i]]*(1-p[i]),dp[i-1][j-1][1]+f[c[i-1]][c[i]]*(1-p[i-1])*(1-p[i])+f[c[i-1]][d[i]]*(1-p[i-1])*p[i]+f[d[i-1]][c[i]]*(1-p[i])*p[i-1]+f[d[i-1]][d[i]]*p[i-1]*p[i]);
}
} 标程
8、2017Day1T3 逛公园(图论)(DP)(记忆化搜索)
题解:https://www.cnblogs.com/fengxunling/p/9860984.html
图论:
1、2008T4 双栈排序(二分图染色)
这道题说实话我是不会做的.......只能看题解啊qwq
(以下有很多话都是摘自题解的,侵删,侵删!)
(看了题解之后发现竟然是个图论题!二分图染色+模拟。)
如果a[i]和a[j]不能在一个栈内,即连接一条i与j之间的无向边,接下来我们只需要判断这个图是否为二分图
由于题目中说编号的字典序要尽可能的小,那么就把编号小的尽可能放到stack1
判断二分图的方法可以采用黑白染色的方式,先从编号小的开始染,第一个顶点染成黑色,相邻的顶点染成不同的颜色,如果发现黑白冲突,那么说明这个图不是一个二分图,是不合法的,输出0.
染色后所有黑色的点进stack1,所有白色的点进stack2,最后模拟输出过程就可以了.
(而如何判断能不能在一个栈内:a[i]和a[j] 不能压入同一个栈\(⇔\)存在一个k,使得 状态:\(f[i]=min(a[i],a[i+1], ... ,a[n])\) 边界条件:\(f[n+1]=INF;\) 状态转移方程:\(f[i]=min(f[i+1],a[i]);\) 于是上述判断就转化为了\(f[j+1] 标程 这是一个分层图的问题,需要构建分层图+dfs(或者bfs)+spfa最短路。 因为我们要执行买入和卖出两个操作,买入之后就不会再买,所以说买入的单次操作之间是独立的,同理卖出的单词操作之间也是独立的。所以我们可以考虑建立分层图。 建立了分层图之后可以保证买入和卖出的操作只进行一次而不是无限多次,(因为买入之后会进入下一层图,卖出之后也会进入下一层图) 我们设第一层图(1~n)是什么都不操作的图,第二层(n+1~2n)是买入的图,第三层(2n+1~3n)是卖出的图。在同一层图进行移动的时候不花费金钱(因为没有进行任何操作),而从第一层进入第二层需要花费金钱(所以我们将第一层和第二层相对应的点(比如说i和i+n)连接需要花费金钱的负边权,同理我们将第二层和第三层相对应的点连接卖出金钱的正边权,之后跑spfa就可以将所有情况覆盖了) 不过也需要注意一点就是买入一定要卖出,但是也可以不买入不卖出(就是不进行任何操作),所以我们要连接一个超级源点3n+1。 这里放上来自fy1234567ok大佬的分层图图片: 本题开两个并查集,先按照冲突值从大到小排序,(冲突值高的优先视作敌人)本着敌人的敌人就是我的朋友的原则,记录每个人的敌人,合并朋友,如果遍历到一个人是另一个人得敌人的话,就将那个人和对方的敌人合并。 标程 这个题就是建图之后,找到每个点,然后将它的子节点两两的乘积加到一起......因为遍历的话需要\(n^2\)复杂度,我们可以考虑乘法分配律优化,注意记录最大值和次大值。 一看到是求两点之间的路径,想到图论。但是用普通的Floyd貌似是时间复杂度会爆炸,所以我们考虑优化。 由于构造树之后我们可以用LCA倍增求得路径,所以我们先构造最大生成树。 构造最大生成树之前将边先排序,然后用树上倍增LCA求出两点之间的路径即可。 最后注意不能到达的话输出-1。 标程 关键是建图的操作不好想。 虽然说是图论,但是实际上就是两遍dfs,第一遍排除不符合性质的点,第二遍求的答案。 标程 这个题当然可以用并查集模拟暴力水80分啦~,但是想要AC的话还是要一定的剪枝!因为我们注意到每一个节点都只有一条出边,所以所有的节点在一起构成了一个基环外向森林,这个东西就是从一个节点出发,最终必定会进入到一个环中。qwq所以我们可以记录环,然后遇到相同的就跳过,这样就大大的降低了复杂度了. 题解:https://www.cnblogs.com/fengxunling/p/9860984.html 不是一个很难的题目,就不放题解了。 题解:https://www.cnblogs.com/fengxunling/p/9759052.html 打暴力其实有80分。。如果是在NOIP考场上,80分性价比已经很高了。 其实这个题可以用STL水到80分,但是STL慢啊!所以我们可以考虑手写堆.......加上优化。 但是如果你想抱紧STL的话,其实我们还可以进行优化来达到减时间的效果。 你可以发现,因为每次蚯蚓的长度都会增加,所以说前面切肯定比后面切最后蚯蚓长度长,所以说本来就存在单调性。 我们假设蚯蚓a1,a2,···,我们排序之后满足a1>a2>····,那么以此分成两只a11,a12,a21,a22,····那么:a12>a22>···,a11>a21>···; 我们可以将没有切的蚯蚓,切的蚯蚓长的那一段,短的那一段分别放在三个优先队列(你想手写堆我也不反对)里面,然后每一次取出三个里面最短的那个,然后切开之后放在对应的队列里面。重复操作,直到到时间为止。 标程 不好意思,目前还不会写。回来补。
$ i2、2009T3 最优贸易(分层图)
(话说还有个分层图的经典题目------> 飞行路线
(飞行路线双倍经验)改造路
借助上图可以更好的理解分层图的方法。
标程3、2010T3 关押罪犯(并查集)(排序)
相似思路NOI2001食物链 BOI2003团伙4、2014Day1T2 联合权值(LCA)(乘法分配律)
核心代码如下:for(int i=1;i<=n;i++)
{
if(v[i].size()<=1) continue;
int cur1=-1,cur2=-1;
for(int j=0;j5、2013Day1T3 货车运输(最大生成树)(LCA)
6、2013Day2T3 华容道(搜索)(图论)
具体见题解:https://www.cnblogs.com/fengxunling/p/9773648.html7、2014Day2T2 寻找道路(图论)(搜索)
8、2014Day1T2 信息传递(图论)(并查集)
核心代码:void search(int now,int bushu)
{
if(pre_v[now]==1) return;
if(v[now]==1)
{
ans=min(ans,bushu-sum[now]);
return;
}
if(!v[now])
v[now]=1;
sum[now]=bushu;
search(fa[now],bushu+1);
pre_v[now]=1;
}9、2017Day1T3 逛公园(图论)(DP)(记忆化搜索)
数据结构
1、2010Day1T2 选择客栈(栈)(递推)
2、2012Day2T3 疫情控制(树)(倍增)(二分)(贪心)(排序)
3、2016Day2T2 天天爱跑步(LCT)(树剖)(线段树)
推荐去看一下这位大佬的博客:https://www.cnblogs.com/ljh2000-jump/p/6189053.html
写的真的很好qwq4、2016Day2T2 蚯蚓(二叉堆)
5、2017Day2T3 列队(平衡树)(树状数组)