时间复杂度和空间复杂度

目录

一. 时间复杂度

有循环的时间复杂度例子：

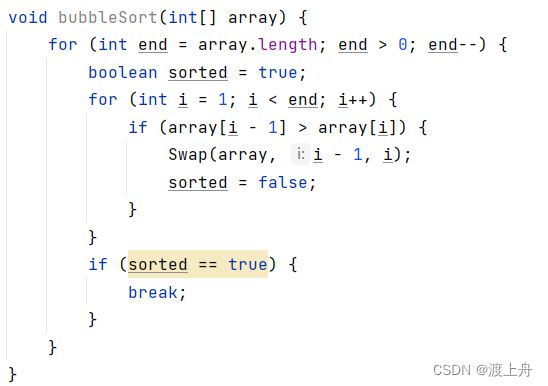
1. 求冒泡排序的时间复杂度？O(n^2)

2. 求二分查找的时间复杂度？O(logn)

3. 求斐波那契数的时间复杂度？O(n) 

​编辑

递归的时间复杂度例子：

1. 递归求阶乘，时间复杂度？O(n)

2. 递归求斐波那契数，时间复杂度？O(2^n)

！！常见的时间复杂度及大小关系：

二. 空间复杂度

有循环的空间复杂度例子：

1. 求冒泡排序的空间复杂度？O(1)

2. 求二分查找的空间复杂度？O(1)

3. 求斐波那契数的空间复杂度？O(n)

递归的空间复杂度例子：

1. 递归求阶乘，空间复杂度？O(n)

2. 递归求斐波那契数，空间复杂度？O(n)

总结

---

一. 时间复杂度

时间复杂度是一个数学函数，定量的描述一个算法的运行时间。

使用大O的渐进表示法来表示时间复杂度 —— 常数看做1，然后找最高次，去系数

有些算法的时间复杂度存在最好、平均和最坏情况，我们平时所说的复杂度指的是最坏情况的时间复杂度

求时间复杂度：找循环，结合代码的思想！如果是递归，那么    递归的时间复杂度 = 递归的次数 * 每次递归之后执行的次数

有循环的时间复杂度例子：

1. 求冒泡排序的时间复杂度？O(n^2)

冒泡排序，最坏情况的时间复杂度：O(n^2)  最好情况下的时间复杂度：O(n)

结合思想，冒泡排序，时间复杂度是个等差数列求和：1+2+3+...+(n-1)

2. 求二分查找的时间复杂度？O(logn)

二分查找，时间复杂度是： O(logn)

每次砍一半，最坏情况，砍到最后只有一个元素时是找的那个元素。

假设砍了x次，只剩那个查找的元素。

那么  n/(2^x) = 1

解出 x = logn（以2为底n的对数）需要砍的次数即时间复杂度

3. 求斐波那契数的时间复杂度？O(n) 

时间复杂度：O(n) 

---

递归的时间复杂度 = 递归的次数 * 每次递归之后执行的次数

递归的时间复杂度例子：

1. 递归求阶乘，时间复杂度？O(n)

递归的次数：n-1

每次递归之后执行的次数：1

时间复杂度：O(n) 

2. 递归求斐波那契数，时间复杂度？O(2^n)

递归的次数: 2^1+2^2+...2^(n-1) = 2^n-2（等比数列求和）

每次递归之后执行的次数：1

时间复杂度：O(2^n) 

！！常见的时间复杂度及大小关系：

O(1)  <  O(logn)  <  O(n)  <  O(nlogn)  <  O(n^2)  <  O(2^n)

二. 空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。

空间复杂度算的是临时变量的个数，本质是衡量一个算法浪费内存的情况，即额外使用的空间。

使用大O的渐进表示法来表示空间复杂度。

有循环的空间复杂度例子：

1. 求冒泡排序的空间复杂度？O(1)

冒泡排序空间复杂度O(1)

循环定义，第二次定义这个变量时，第一次定义的已经被回收了。因为循环结束，局部变量会被回收。所以，sorted，i，end 这些变量都是常数项，来来回回其实每个只浪费了一个额外空间，一共浪费3个空间。所以空间复杂度是O(1)。

2. 求二分查找的空间复杂度？O(1)

二分查找的空间复杂度O(1)

3. 求斐波那契数的空间复杂度？O(n)

空间复杂度：O(n)

因为额外创建了一个数组fibArray，使用了额外的空间。循环定义的变量算常数项忽略不计。

递归的空间复杂度例子：

1. 递归求阶乘，空间复杂度？O(n)

每次递归，都会调用一次这个函数，都会在栈上开辟一个空间，开辟了 n-1 个空间，

所以空间复杂度是O(n) 

2. 递归求斐波那契数，空间复杂度？O(n)

每次递归，都会调用一次这个函数，都会在栈上开辟空间。但函数执行完，也就是“归”时，开辟的空间就被回收了。

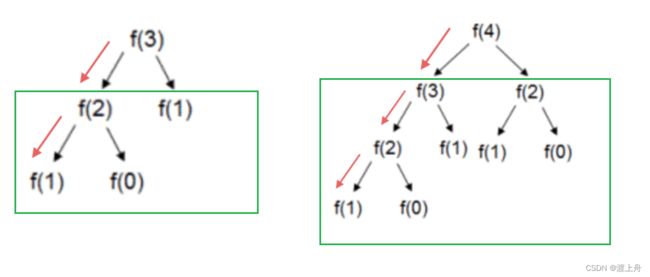
让我们先来看一下执行过程：（以n为3时举例）

想要计算f(3)的结果，会先执行完左侧的f(2)返回结果，才会去执行右侧的f(1)

而想计算f(2)的结果，需要先执行完左侧f(1)返回结果，才会去执行右侧f(0)，

f(1)和f(0)都执行完返回结果了，f(2)才算执行完

执行完f(2)，才会去执行右侧f(1)

也就是说，会按照“箭头”一路走到底，一直走到能“归”。这段是一直开辟空间的。此时开辟了2块临时空间。

而f(1)执行完返回结果后，这个空间就会被回收，这时候去执行f(0)，开辟一块空间。虽然执行f(0)开辟了一块空间，但是此时f(1)开辟的空间已经被回收了，临时空间并没有增加，还是只额外浪费了一块。可以理解为空间是可以重复利用的，f(1)回收的空间又被f(0)用了，f(1)和f(0)实际上只浪费了一块空间。

所以说，其实每一层只额外浪费了一块空间。当n为3时，事实上一共只额外开辟了2块空间。我们也可以知道，当n为4时，浪费了3块空间。

所以，递归求斐波那契数，会额外使用n-1个空间

空间复杂度：O(n)

总结

冒泡排序：                              时间复杂度O(n^2)                 空间复杂度O(1)

二分查找：                              时间复杂度O(logn)                空间复杂度O(1)

循环求斐波那契数：                时间复杂度O(n)                     

递归求斐波那契数：                时间复杂度O(2^n)                 空间复杂度O(n)

递归求阶乘：                           时间复杂度O(n)                     空间复杂度O(n)