特征值与特征向量_线性变换（三）【特征值与特征向量】
笔者是一个数学系的在读本科生，若是文章中有纰漏，欢迎指出。特征向量与特征值www.bilibili.com
本篇笔记仅供交流学习。
在正式开始本篇笔记之前，按照惯例，还是先推荐你观看 3Blue1Brown的线性代数的本质（Essense of Linear Algebra）系列在特征值与特征向量这一主题下的视频：
特征值与特征向量
一、特征值和特征向量的定义
特征值_百度百科上如此定义特征值：
特征值是线性代数中的一个重要概念。在数学、物理学、化学、计算机等领域有着广泛的应用。
设 A 是n阶方阵，如果存在数m和非零n维列向量x，使得 Ax=mx 成立，则称 m 是A的一个特征值或本征值。
非零n维列向量x称为矩阵A的属于特征值m的特征向量或本征向量，简称A的特征向量或A的本征向量。
特征向量_百度百科上如此定义特征向量：
数学上，线性变换的特征向量（本征向量）是一个 非简并的向量，其方向在该变换下不变。该向量在此变换下缩放的比例称为其特征值（本征值）。
非简并系_百度百科上如此定义非简并系：
若一个体系没有两个或两个以上 线性无关的本征函数对应于某一力学量（通常指其哈密顿量）的同一本征值，则称此体系的量子态为非简并态。这样的体系为非简并系。
（奈何笔者水平有限，无法对这个定义作出更详细的解释，故笔者只能尝试用自己的理解向你介绍特征值与特征向量的概念。
二、特征值和特征向量的定义（笔者理解）
笔者是这样理解特征向量的：
所谓特征向量，就是线性空间V中经过了线性变换A之后，并 未发生旋转与偏移，且 未离开它张成的直线的全部向量的集合。
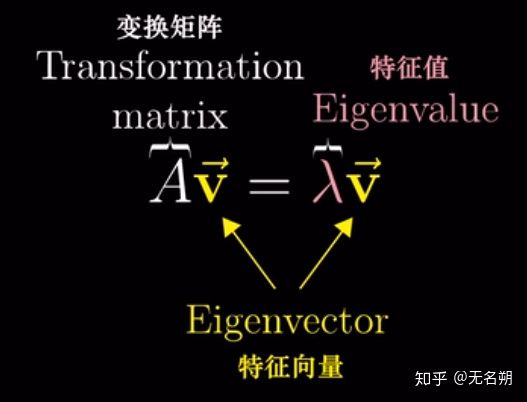
那么为什么笔者会这样理解呢？我们先来看看下面这幅图。
这个等式的意义是，矩阵A与特征向量向量v的乘积，等于特征向量v乘某个数λ。
而每个特征向量都有对应的数λ，这个λ称为特征值。
我们知道，矩阵A相当于一个线性变换，相当于对空间上的向量进行旋转/缩放/投影等操作；而λ是一个常数，λ的数乘相当于对某个向量进行缩放操作（向量仍在原本所在的直线上）。
那么这个等式的几何意义就是，对线性空间V中所有的向量进行了线性变换A之后，方向并未偏移（可以反向），且向量模长变为了原来的λ倍的向量，称为λ对应的特征向量！
三、特征值与特征向量的几何意义与性质
也许你看完上面这个解释之后仍觉得不是很直观，下面笔者将借助3Blue1Brown的线性代数的本质（Essense of Linear Algebra）系列的截图为你详细解读一下特征向量的几何意义。
首先，我们回到开头的那条等式。
等号左侧表示一个矩阵与一个向量的乘积，而等号的右侧表示一个向量的数乘。
我们不妨也构造一个矩阵B，使得矩阵B的作用效果与λ数乘的效果相同，那么可以想象，矩阵A与矩阵B的作用效果也相同。
而与λ数乘的效果相当于向量v的每一个分量都变成了原来的λ倍，因此，我们可以构造这样的对角矩阵B：
通常我们把对角矩阵B写作上式，I为恒等变换（单位变换）。
所以我们就可以得到等式：
移项之后得到：
而这也就是笔者初学这一概念时，对λ对应的特征向量仅有的理解：“使得(A-λI)X=0方程成立的向量集合”。
接下来，我们就去找向量v，使得这个等式成立。
易知，v为零向量时等式显然成立。
然后我们再去找非零向量使得这条等式成立，由克拉默法则易知，即要令（A-λI）的行列式为零。
关于如何直观理解行列式为零的线性变换，以及这个变换之后向量的位置分布，笔者强烈推荐你观看下面这个视频：
逆矩阵，零空间、列空间www.bilibili.com如果你不方便看也无妨，笔者在这里简单地向你解释一下。我们知道，线性变换相当于对一个线性空间进行投影、缩放、旋转等操作，而行列式正是线性变换的伸缩因子。
以二维空间为例，当线性变换A对应的矩阵行列式为零时，线性变换A相当于把这个二维空间压到了更低维度的空间。
特别地，当这个矩阵的秩为1时，线性变换A相当于把这个二维空间压成了一条直线，也就是所谓的“降维打击”。
以此类推，当这个矩阵的秩为0时，线性变换A相当于把这个二维空间压成了一个点。
（矩阵可逆的概念也来自于此，没有任何线性变换可以将低维空间变换至高维，我们不难想象，若一条直线经过某个线性变换张成了一个空间，那么原本直线上的某个向量便要对应张成空间内某条直线上的所有点，这是典型的“一对多”，不符合我们对线性变换的定义）
由于我们在研究特征向量的问题时，对于一个确定的数λ，我们希望找到的是数乘了λ的那些向量张成的那条直线。因此，构造行列式为0，排除原有空间中的干扰因素，找到那条直线，这就是我们想做的。
而我们通过我们构造得到的含λ的多项式，就称为λ对应的特征多项式。
四、特征值与特征向量的性质
线性变换的矩阵不一定有特征向量，如：逆时针旋转90°的线性变换中，每个矩阵都发生了方向的偏移，自然也就找不到对应的特征向量了。
特征值的代数重数（该特征值在特征多项式中的次数）大于等于特征值的几何重数（该特征值对应线性无关的特征向量个数）。
【这个性质的严谨证明过程用电脑敲起来比较麻烦，在后续的笔记中如果有时间的话笔者再做详细解析】
每个特征值对应无数个特征向量。（一条直线上有无数个点，在这上面缩放程度相同的也有无数个向量）
每个特征向量唯一对应一个特征值。（未发生偏移，且缩放程度相同的向量都落在同一条直线上）
属于单个特征值的特征向量可以不止在一条直线上，举个例子，让线性空间V内所有的向量都变成原来的两倍。
五、特征基
当特征向量恰好是其作用的线性空间的基向量时，我们可以得到这样的矩阵，矩阵的对角元是它们所属的特征值（每个特征向量对应的缩放程度）。
而这样的一组特征向量，我们称为：特征基。
写成对角阵的好处是，这种矩阵在连乘的时候可以进行自己与自己的累乘，比如：
如果你线性无关的特征向量个数足够能张成全空间（个数等于全空间的维数），那么你就可以变换你的坐标系，使得这些特征向量就是基向量。
如何实现这个变换呢？上一篇笔记的结尾已经告诉你答案了
那就是，应用“A逆乘以M乘以A”的转移。
也就是说，以特征向量为基构建基变换矩阵A，然后矩阵M为原本的线性变换，显然得到的是同一个变换，而这个变换，
就是从新基向量所构成的坐标系的角度来看的！！！！
而得到的新矩阵，必定是对角矩阵！这是因为，它所处的坐标系的基向量在变换中只进行了缩放，对应的线性空间内的每一个向量必定也都只进行了缩放。
六、特征值与特征向量的应用
在三维空间中，如果你能找到一个三维物体旋转的特征向量，那么你就相当于找到了这个旋转的旋转轴。（只有轴上的向量并未发生旋转与偏移）
特别一提，“旋转”这个线性变换的特征值为1，因为旋转这个操作并不缩放任何一个向量。
最后，衷心希望这篇笔记对你有帮助。