基础算法入门11——数据结构模拟2

• Trie树
• 并查集
• 堆
• 模拟堆

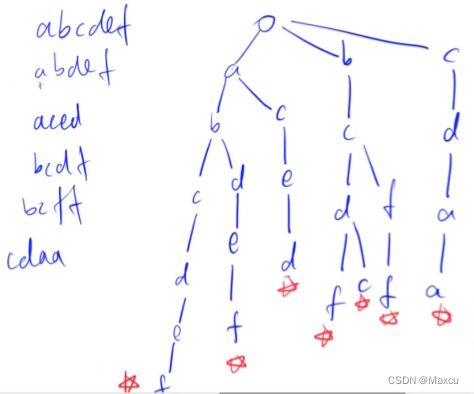
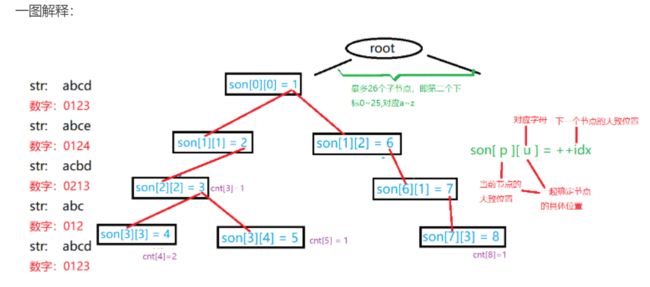
Trie树

用来快速存储和查找字符串集合的数据结构

#include
using namespace std;
const int N=100010;
int son[N][26];//将整个trie树存储下来
int cnt[N];//cnt[i]统计以节点i作为结尾的字符串的出现次数，也就是单个字符传出现的次数
char str[N];//存储字符串
int idx;//表示当前的节点编号
void insert(char q[])
{
    int p=0;//p用来模拟指针，从根节点开始
    for(int i=0;q[i];i++)
    {
        int u=q[i]-'a';//将每个字母映射到'0-25'这26个数字
        if(son[p][u]==0)son[p][u]=++idx;//创建新的节点
        p=son[p][u];//指针向下移动
    }
    cnt[p]++;//为这个字符串的结尾的节点做标记
}
int query(char q[])
{
    int p=0;
    for(int i=0;q[i];i++)
    {
        int u=q[i]-'a';
        if(!son[p][u])return 0;//说明这个字符串不存在
        p=son[p][u];//不停的移动p指针
    }
    return cnt[p];//返回这个字符串出现的次数
}
int main()
{
    int n;
    cin>>n;
    char op[2];
    while (n -- )
    {
        cin>>op>>str;
        if(op[0]=='I')insert(str);
        else cout<<query(str)<<endl;
    }
    return 0;
}

并查集

一共有 $n$ 个数，编号是 $1\sim n$，最开始每个数各自在一个集合中。

现在要进行 $m$ 个操作，操作共有两种：

1. M a b，将编号为 $a$ 和 $b$ 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略个操作；
2. Q a b，询问编号为 $a$ 和 $b$ 的两个数是否在同一个集合中；

输入格式

第一行输入整数 $n$ 和 $m$。

接下来 $m$ 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 $a$ 和 $b$ 在同一集合内，则输出 Yes，否则出 No。

每个结果占一行。

数据范围

$1\le n,m\le 10^5$

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

并查集是主要是用来快速的合并集合，以及判断元素是否是属于同一个元素

实现的原理：

• 将每个集合用树存储
• 每个节点存的是父节点的地址，根节点的值就是根节点地址
• 根节点的值等于根节点本身的地址，也就是说，根节点的值就是整个集合的标志，那么判断两个元素是否属于同一个集合，就可以通过直接判断两个元素的根节点的值是否相同

• 用一个数组来存储每个节点的父节点，初始化，每个节点的父节点是自己本身，也就是每个节点本身就是一个集合
• 判断一个节点是不是根节点

判断一下
f[x]==x

• 找到一个节点的根节点（祖宗节点）f[f[f[f[f[f[f[x]]]]]]…] 采取递归的操作

• 同时加速：每次查找到一个节点的祖宗节点，直接将该节点指向自己的祖宗节点（祖宗秒变父）（路径压缩）

• 合并集合：将a集合的根节点的父节点由指向自己指向b集合的根节点

#include
using namespace std;
const int N=1000010;
int f[N],idx;
int find(int x)//每次进行一次find，这里的递归操作就会进行一次路径压缩，每个元素的父节点都变成了自己的根节点
{
    if(x!=f[x]) f[x]=find(f[x]);//如果编号x的节点不是根节点，那么就递归查找到自己的根节点，根节点变成父节点
    return f[x];//返回父节点（根节点）
}

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)f[i]=i;
    while(m--)
    {
        char op[2];
        int a,b;
        cin>>op>>a>>b;
        if(op[0]=='M') f[find(a)]=find(b);//将a节点的根节点的父节点设置成b的根节点，这样a和b所在的集合就合并
        else 
        {
            if(find(a)!=find(b))cout<<"No"<<endl;//两个节点的根节点的值不同
            else cout<<"Yes"<<endl;
        }
    }
    return 0;
}

堆

• 插入一个数
• 求出集合中的最小值
• 删除最小值
• 删除任意一个元素
• 修改任意一个元素

堆是一个二叉树（完全二叉树）

规定每个节点都不大于自己的子节点的值

最基本的两个操作是up和down操作

堆的一个基本结构是二叉树，我们要保证根节点的值是最小的，每个结点的值都小于它的左右两个子节点

根节点的下标是1

设某个节点的下标为x 则它的左儿子下标就是x*2,右儿子的下标就是x*2+1

up操作就是，如果我们要对一个节点的值进行操作，如果这个操作后的节点的值变小了，我们就需要对它进行up

也就是把它对他的父节点进行比较，如果比父节点小，那么就要把这个节点和父节点进行值得交换，用来保证整个堆从上到下是一个值从小到大的趋势，保证父节点大于等于子节点的值

down操作就是反过来，如果我们要对一个节点的值进行操作，如果这个操作后的节点的值变大了，我们就需要对它进行down操作，让它与自己的两个左右子节点中的最小值进行交换操作

堆排序的代码：
堆排序就是每次输出堆中的根节点（堆的最小值），然后删掉根节点，对堆重新整理一下，然后再输出根节点（此时堆的最小值），这样循环下去就能得到堆排序后的结果。

#include 
#include 
#include 
using namespace std;
const int N=100010;
int h[N],s;
int n,m;
void down(int x)
{
    int t=x;
    if(x*2<=s&&h[x*2]<h[t])t=x*2;//左儿子存在，并且左儿子的值比t小
    if(x*2+1<=s&&h[x*2+1]<h[t])t=x*2+1;//右儿子存在，并且右儿子的值比t小
    if(t!=x)
    {
        swap(h[x],h[t]);
        down(t);//对子节点进行down
    }
}

void up(int x)
{
    while(x/2&&h[x/2]>h[x])
    {
        swap(h[x/2],h[x]);
        x/=2;
    }
}

int main()
{
    cin>>n>>m;
    for(int i =1;i<=n;i++)cin>>h[i];
    s=n;
    
    for(int i=n/2;i;i--)down(i);
    //从整个堆的倒数第二层向上对每个节点进行down()把时间控制到log(n)
    
    for(int i=1;i<=m;i++)
    {
        cout<<h[1]<<" ";
        h[1]=h[s--];//将最后一个值作为根节点的值，再对这个根节点做一次down
        down(1);
    }
    
    return 0;
    
}

模拟堆（关于堆的所有操作）

维护一个集合，初始时集合为空，支持如下几种操作：

1. I x，插入一个数 $x$；
2. PM，输出当前集合中的最小值；
3. DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
4. D k，删除第 $k$ 个插入的数；
5. C k x，修改第 $k$ 个插入的数，将其变为 $x$；

现在要进行 $N$ 次操作，对于所有第 $2$ 个操作，输出当前集合的最小值。

输入格式

第一行包含整数 $N$。

接下来 $N$ 行，每行包含一个操作指令，操作指令为 I x，PM，DM，D k 或 C k x 中的一种。

输出格式

对于每个输出指令 PM，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

数据范围

$1\le N\le 10^5$
$-10^9\le x\le 10^9$
数据保证合法。

输入样例：

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例：

-10
6

由于题目说的是查询第k次操作，因此我们需要记录某个节点是第几次插入的。

所有操作实现方式

• 插入数据，将新节点插到队尾，然后再对这个新节点进行up操作
• 输出最小值，直接将树的根节点输出
• 删除最小值，用最后的节点覆盖根节点，size–，然后对根节点进行down操作
• 删除任意节点，用最后一个节点覆盖这个节点，然后对这个节点进行up和down操作，虽然看上去是两个操作都要进行，实际上只会进行一次操作，这里是直接省略掉了一些判断操作，更为简便。
• 修改任意节点的值，先修改，再进行up and down操作

这里由于要记录节点是第几次插入的，因此需要额外的数组（见代码）

#include
#include
using namespace std;
const int N=1000010;
int h[N],ph[N],hp[N];
//ph数组存的是第k次插入的值是几号节点，ph[k]=idx 第k次插入的是idx节点
//hp数组存的是这个节点是第几次插入的，hp[idx]=k，idx节点是第k次插入的
int cnt;
void heap_swap(int a,int b)//除了简单交换两个节点值，还要交换两个节点是第几次插入的相关信息
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a],hp[b]);
    swap(h[a],h[b]);
}
void up(int x)
{
    while(x/2&&h[x/2]>h[x])
    {
        heap_swap(x,x/2);
        x/=2;
    }
    
}
void down(int x)
{
    int t=x;
    if(x*2<=cnt&&h[x*2]<h[t])t=x*2;
    if(x*2+1<=cnt&&h[x*2+1]<h[t])t=x*2+1;
    if(x!=t)
    {
        heap_swap(t,x);
        down(t);
    }
}

int main()
{
    int n;
    cin>>n;
    int m=0;//统计插入次数
    while (n -- )
    {
        string op;
        cin>>op;
        int x,k;
        if(op=="I")//插入新的数据
        {
            cin>>x;
            h[++cnt]=x;
            m++;
            ph[m]=cnt,hp[cnt]=m;
            up(cnt);
        }
        else if(op=="PM")//显示最小值
        {
            cout<<h[1]<<endl;
        }
        else if(op=="DM")//删除最小值
        {
            heap_swap(1,cnt);
            cnt--;
            down(1);
        }
        else if(op=="D")//删除第k次插入的数据
        {
            cin>>k;
            k=ph[k];
            heap_swap(k,cnt);
            cnt--;
            up(k);
            down(k);
        }
        else //将第k次插入的数据修改
        {
            cin>>k>>x;
            k=ph[k];
            h[k]=x;
            down(k);
            up(k);
        }
        
    }
    return 0;
}

总结

• Trie树是用来存储字符串，同时对字符串进行快速的查询操作
• 并查集是用来进行集合的存储，对不同的集合进行快速合并，对元素是否处于同一个集合进行快速判断，重点是find函数
• 堆，它的特点是

1. 他是完全二叉树
2. 根节点是树中最小的值
3. 每个节点的值都小于自己的左右两个子节点
   主要是要记住两个up和down操作