【数据结构篇】手摸手带你学会如何手写一个栈
文章目录
- 栈
-
- 1、栈的基本介绍
- 2、栈的实现
-
- 2.1 手写顺序栈
- 2.2 手写链栈
- 3、练习
栈
1、栈的基本介绍
-
什么是栈?
栈(stack)又名堆栈,它是一种运算受限的线性表,它只允许再表的一端进行插入和删除操作,这一端也称作栈的栈顶(Top),另一端称作栈底(Bottom)。
-
栈的特点:栈中的数据元素先进后出(Last In First Out),所以也称栈为LIFO表
-
栈的分类:顺序栈 和 链栈
- 顺序栈是指使用顺序存储结构实现的栈
- 链栈是指使用链式存储结构实现的栈
-
栈的应用:表达式求值、回溯功能的实现
-
栈的基本操作:
boolean push(E item):出栈,获取栈顶的元素(栈中元素减一)boolean pop():入栈,向栈中添加一个元素E peek():取栈顶元素,获取栈顶的元素(栈中元素个数不变)int size():获取栈中元素的个数boolean isEmpty():判断栈中是否为空
2、栈的实现
测试类:
package com.hhxy.stack.sequence;
import java.util.Scanner;
public class StackTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
SequenceStack stack = new SequenceStack(3);
OUT: while (true) {
System.out.println("------------欢迎来到栈的操作界面---------------");
System.out.println("请输入你的指令:");
System.out.println("0 : 退出程序");
System.out.println("1 : 入栈");
System.out.println("2 : 出栈");
System.out.println("3 : 取栈顶元素");
System.out.println("4 : 获取栈中元素的个数");
System.out.println("5 : 展示栈中所有的元素");
System.out.println("6 : 清空栈");
switch (sc.next()) {
case "0":
System.out.println("正在退出程序~~~");
break OUT;
case "1":
System.out.println("请输入要入栈的元素:");
int n = sc.nextInt();
stack.push(n);
break;
case "2":
try {
System.out.println("出栈的元素是:"+stack.pop());
}catch(Exception e) {
System.out.println(e.getMessage());
}
break;
case "3":
try {
System.out.println("当前栈顶元素是:"+stack.peek());
}catch(Exception e) {
System.out.println(e.getMessage());
}
break;
case "4":
try {
System.out.println("当前栈中的元素个数为:"+stack.size());
}catch(Exception e) {
System.out.println(e.getMessage());
}
break;
case "5":
stack.show();
break;
case "6":
if(stack.clear()) System.out.println("栈已清空");
break;
default:
System.out.println("请输入有效指令!");
break;
}
}
sc.close();
System.out.println("程序已退出");
}
}
效果展示:
2.1 手写顺序栈
顺序栈和顺序队列的实现极其相似,都是使用数组来存储数据的,出栈并不是整整意义的删除了栈中的元素,再数组中它仍然存在,也就是说当栈中元素为满时,出栈后,后续的入栈只是将原来数组中所在位置的元素进行了覆盖!
- 栈顶初始值:
top = -1- 栈空判断:
top == -1- 栈满判断:
top == maxSize-1- 出栈:
top--- 入栈:
++top
实现代码:
package com.hhxy.stack.sequence;
/**
* 顺序栈的实现
* 使用数组
* @author ghp
*
*/
public class SequenceStack {
private int maxSize;//栈的最大容量
private int[] arr;//存储入栈的元素
private int top;//指向栈顶的指针
public SequenceStack(int maxSize) {
this.maxSize = maxSize;
top = -1;
arr = new int[maxSize];
}
/**
* 判断栈是否已满
* @return true表示已满
*/
public boolean isFull() {
// if(top != maxSize-1) {
// return false;
// }
// return true;
return top == maxSize-1;
}
/**
* 判断栈是否为空
* @return true表示为空
*/
public boolean isEmpty() {
return top == -1;
}
/**
* 入栈
* @return true表示入栈成功
*/
public boolean push(int n) {
if(isFull()) {
return false;
}
arr[++top] = n;
return true;
}
/**
* 出栈
* @return true表示出栈成功
*/
public int pop() {
if(isEmpty()) {
throw new RuntimeException("栈为空,无法出栈");
}
return arr[top--];
}
/**
* 取栈顶元素
* 注意:只是获取,并不需要减少栈中的元素
*/
public int peek() {
if(isEmpty()) {
throw new RuntimeException("栈为空,无法出栈");
}
return arr[top];
}
/**
* 获取栈中元素的个数
* @return
*/
public int size() {
int count = 0;//记录栈中元素的个数
for (int i = 0; i <= top; i++) {
count++;
}
return count;
}
/**
* 展示栈中所有的元素
* 注意:需要从栈顶开始展示
*/
public void show() {
if(isEmpty()) {
System.out.println("栈为空!");
return;
}
for (int i = top; i >= 0; i--) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
/**
* 清空栈中元素
*/
public boolean clear() {
top = -1;
return true;
}
}
2.2 手写链栈
使用链式存储结构实现栈相较于使用顺序存储结构而言,最大的好处就是不用考虑为满的情况。它的实现也相对简单,就是不断操作头指针,让链表只能在头节点进行插入和删除,具体步骤如下图所示:
测试类只要改这里就行了:
实现代码:
package com.hhxy.stack;
/**
* 使用链表实现栈 备注:使用的是不带头节点的链表
* 这种在链表头部进行插入的方法称作头插法
* @author ghp
*
*/
//结点类
class Node {
// 将成员公有化,方便访问
public int n;// 数据域
public Node next;// 引用域
public Node() {
}
public Node(int n) {
this.n = n;
}
@Override
public String toString() {
return "[n=" + n + "]";
}
}
//链表类
public class LinkStack {
Node top = null;//创建一个头指针(主要不要创成结点了,不然就成带头节点的链表了)
/**
* 判断栈是否为空
*
* @return true表示为空
*/
public boolean isEmpty() {
return top == null;
}
/**
* 入栈
*
* @return true表示入栈成功
*/
public boolean push(int n) {
Node newNode = new Node(n);// 将需要新增加的数据放到一个新建结点中,然后使之成为头节点
newNode.next = top;
top = newNode;// 将头指针指向新的头节点
return true;
}
/**
* 出栈
*
* @return true表示出栈成功
*/
public int pop() {
if (isEmpty()) {
throw new RuntimeException("栈为空,无法出栈");
}
int t = top.n;// 临时存储头节点的值,方便头指针移位
top = top.next;
return t;
}
/**
* 取栈顶元素 注意:只是获取,并不需要减少栈中的元素
*/
public int peek() {
if (isEmpty()) {
throw new RuntimeException("栈为空,无法出栈");
}
return top.n;
}
/**
* 获取栈中元素的个数
*/
public int size() {
int count = 0;// 记录栈中元素的个数
Node current = top;// 使用辅助指针用来遍历链表,防止链表错位
while (current != null) {
count++;
current = current.next;
}
return count;
}
/**
* 展示栈中所有的元素 注意:需要从栈顶开始展示
*/
public void show() {
if (isEmpty()) {
System.out.println("栈为空!");
return;
}
Node current = top;
while (current != null) {
System.out.print(current.n+" ");
current = current.next;
}
System.out.println();
}
/**
* 清空栈中元素
*/
public boolean clear() {
if(top == null) {
return true;
}
//方式一:直接另头指针指向空,这种方式虽然简单,省时间但是费内存
// top.next = null;
// top = null;//切记要将top置为空
//方式二:将每个结点的引用域都设为空,这种方式复杂,费时间但是省内存
Node current = top;//辅助遍历链表
Node temp = top;//临时存储top的引用,防止链表断裂
//切记先要将top设为null
top = null;
while(current.next != null) {//注意最后一个结点不需要设为空,不然会出现空指针异常
temp = temp.next;
current.next = null;
current = temp;
}
return true;
}
}
拓展知识:逆波兰表达式
3、练习
任务:使用栈实现一个的计算器
要求:任意输入一个四则运算的表达式(这个表达式必须是中缀表达式),能够得出正确的结果
主要实现步骤:
-
通过一个 index 值(索引),来遍历我们的表达式
-
如果我们发现是一个数字, 就直接入数栈
-
如果发现扫描到是一个符号, 就分如下情况讨论:
-
1 如果发现当前的符号栈为空,就直接入栈
-
2 如果符号栈有操作符就进行比较,继续分类讨论:
3.2.1 如果当前的操作符的优先级小于或者等于栈中的操作符, 就需要从数栈中pop出两个数,在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈;
3.2.2 如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈
-
-
当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并依次进行运算
-
最后在数栈只有一个数字,就是表达式的最终结果
示意图:
实现代码:
所用的数组也是2中的。
package com.hhxy.stack;
import java.util.Scanner;
public class Calculator {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入需要计算的表达式(中缀表达式):");
String expression = sc.nextLine();
//0、创建一个数字栈和一个字符栈
//使用顺序栈
// SequenceStack intStack = new SequenceStack(10);
// SequenceStack charStack = new SequenceStack(10);
//使用链栈
LinkStack intStack = new LinkStack();
LinkStack charStack = new LinkStack();
int index = 0;//用来遍历表达式expression的指针
int number1 = 0;//临时存储表达式中的指
int number2 = 0;
char oper = ' ';//临时存储表达式中的符号
int result = 0;//运算返回的结果
//1、扫描遍历表达式expression
while(index < expression.length()) {
//2、依次获取表达式中的字符
char ch = expression.substring(index, index+1).charAt(0);
//3、判断是字符还是数字,字符入字符栈,数字入数字栈
if(isOper(ch)) {
//3.1 如果是运算符,需要判断字符栈中是否为空
if(charStack.isEmpty()) {
//3.1.1 如果字符栈为空,直接入栈
charStack.push(ch);
}else {
//3.1.1 如果字符栈不为空,让表达式中的符号和字符栈栈顶的符号进行优先级比较
if(priority(ch) <= priority(charStack.peek())) {
//3.1.2 如果优先级小于等于字符栈栈顶的符号,则取出数栈中两个数,以及字符栈的栈顶符号进行运算
number2 = intStack.pop();
number1 = intStack.pop();
oper = (char) charStack.pop();
//进行运算
result = calculate(number1, number2, oper);
//同时将运算结果入数栈中,字符入字符栈中
intStack.push(result);
charStack.push(ch);
}else{
//3.1.2 如果优先级高于字符栈栈顶的符号,直接将符号入栈
charStack.push(ch);
}
}
}else {
//3.1 如果是数字,直接入数栈(注意:要数据类型转换)
intStack.push(ch-48);
}
index++;//索引后移,接着获取字符串后一个字符
}
//4、当字符串扫描完毕,就将两个栈中剩下的所有元素进行运算
while(!charStack.isEmpty()) {//当符号栈为空时,数栈中只有一个最终的结果,此时运算完毕
number2 = intStack.pop();
number1 = intStack.pop();
oper = (char) charStack.pop();
result = calculate(number1, number2, oper);
intStack.push(result);
}
//5、测试一下结果
result = intStack.pop();
System.out.println("表达式"+expression+"的计算结果为:"+result);
}
/**
* 判断是否是运算符
* @return true表示是运算符
*/
public static boolean isOper(char oper) {
return oper == '+' || oper == '-' || oper == '*' || oper == '/';
}
/**
* 判断运算符的优先级
* @return 返回一个数字来表示字符的优先级,数字越大优先级越高
*/
public static int priority(int oper) {
if(oper == '*' || oper == '/') {
return 1;
}else if(oper == '+' || oper == '-') {
return 0;
}else {
return -1;//假定只有加减乘除四则运算
}
}
/**
* 进行四则运算
* @param operation 运算符
* @param number1 靠经栈底的那个数
* @param number2 两者之间上面的数
* @param oper 运算符号
* 一定要注意number1和number2的顺序,传参时也一样,不然很容易入坑,还不容易被发现!
*/
public static int calculate(int number1,int number2,int oper) {
int result = 0;//运算结果
switch (oper) {
case '+'://case相当于是==号进行比较,相当于是直接比较编码
result = number1+number2;//一定是靠近栈底的数在前面,可以画图琢磨
break;
case '-'://case相当于是==号进行比较,相当于是直接比较编码
result = number1-number2;//一定是靠近栈底的数在前面,可以画图琢磨
break;
case '*'://case相当于是==号进行比较,相当于是直接比较编码
result = number1*number2;//一定是靠近栈底的数在前面,可以画图琢磨
break;
case '/'://case相当于是==号进行比较,相当于是直接比较编码
result = number1/number2;//一定是靠近栈底的数在前面,可以画图琢磨
break;
default:
break;
}
return result;
}
}
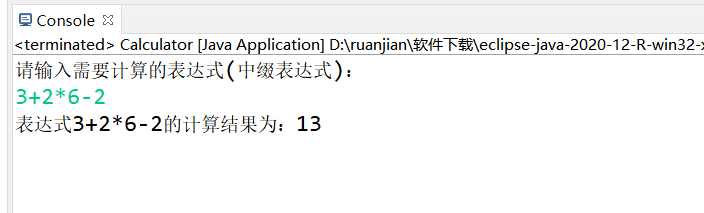
上面代码存在一个致命的弊端w(゚Д゚)w,那就是计算只能计算一位数的四则运算,多位数就会出错,比如这个:
代码优化:
主要对一下几个地方进行了改动:
Hi~ o( ̄▽ ̄)ブ现在就能进行多为数的运算了
效果检验:
知识拓展::前缀表达式、中缀表达式、后缀表达式
给定一个正常的表达式:
(3+4)*5-6/2
前缀表达式(波兰式):运算符在参与运算的数字前面的表达式。前缀表达式表示法:
- * + 3 4 5 / 6 2所用算法:从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素,栈顶 ? 次栈顶),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果
中缀表达式:运算符在参与运算的数字之间的表达式。中缀表达式表示法:
(3+4)*5-6/2实现算法:前面
后缀表达式(逆波兰式):运算符在参与运算的数字后面的表达式。后缀表达式表示法:
3 4 + 5 * 6 2 / -所用算法:从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素,次栈顶 ? 栈顶),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
三种方式相比较:前缀和后缀都是符合计算机思维的,而中缀是符合人类思维的,从这一点触发,两者各有优点,但总的来讲还是前缀和后缀号,因为除了中缀表达式的可读性高外,它的运算效率(算法的时间复杂度)远远低于前缀和后缀