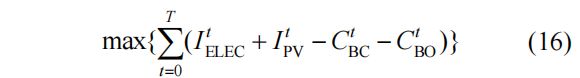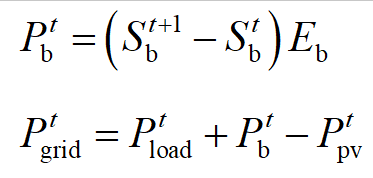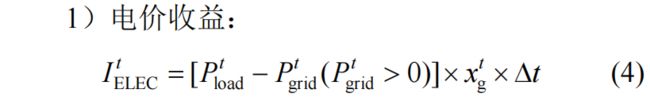(文章复现)建筑集成光储系统规划运行综合优化方法matlab代码
参考文献:
[1]陈柯蒙,肖曦,田培根等.一种建筑集成光储系统规划运行综合优化方法[J].中国电机工程学报,2023,43(13):5001-5012.
1.基本原理
本文建立的双层耦合模型内、外层分别对应求解容量配置与能量调度问题。外层模型设置光伏与储能容量备选集并将容量配置组合传递给内层,内层模型求解当前容量组合下经济性最优的能量调度结果与日运行收益并反馈给外层。外层模型计及BIPV 系统全寿命周期成本与效益,以投资回收期最短为目标函数,优化光伏与储能的容量配置。双层耦合模型的结构如图 1 所示。
根据建筑所在地经纬度,通过 NASA POWER网站获取单位小时太阳辐射量数据,根据光电转换率与光伏系统效率计算得到典型光伏日出力数据。外层模型设置光伏与储能容量备选集,其中光伏容量以光伏板面积表示,选取某一容量组合[APV, Eb],其中 APV为集合{A0,A0+ΔA,…,Amax}中某一取值,Eb在集合{E0,E0+ΔE, …,Emax}中取值,并传递给内层模型。内层模型在当前容量配置下,根据建筑 1 日用电分布等参数,以储能电池 25h 的荷电状态作为优化参数(初值与末值相等且都设置为 0.5),日运行收益最大作为优化目标,利用改进粒子群算法(particle swarm optimization,PSO)进行求解,得到24h内建筑集成光储系统的能量调度结果与日运行最大收益并反馈给外层模型。外层模型据此计算当前容量配置组合下的最短投资回收期,再选取下一个容量组合,重复上述过程。遍历备选集所有的容量组合,投资回收期作为评价标准,即可获得最优光伏–储能容量配置组合与该组合对应的最优能量调度策略。
1.1优化指标
采用投资回收期作为优化目标,综合考虑系统全寿命周期各阶段的成本与效益。
1.1.1 系统成本
系统成本主要包括光伏与储能的建设成本与运维成本。
1)储能建设成本。
内层模型计及储能充放电成本,即将储能建设阶段的投资折算到一日循环充放电产生的成本,其计算式为
2)储能运维成本。
储能维护成本包括日常运维、零部件更换、人工等费用,利用建设成本乘以比例系数ηB得到,计算式为
3)光伏建设与年度运维成本。
光伏建设成本包括光伏组件、逆变器、缆线、辅材等费用及人工安装费。运维成本包括器件维护费用及人工成本,对应比例系数为ηPO,计算式为
1.1.2 系统收益
系统收益包括电价收益、光伏上网收益、政府补贴、碳减排收益与光伏组件回收收益。
4)碳减排收益。
碳交易是温室气体排放权交易的统称,2005年《京都议定书》将市场机制作为解决全球温室气体减排问题的新路径,即把二氧化碳排放权作为一种商品,从而形成了二氧化碳排放权的交易[15-16]。
1.2目标函数
1.2.1 外层模型目标函数
外层模型以整个系统的投资回收期最短作为优化目标,其函数表达式为
1.2.2 内层模型目标函数
内层模型根据 1 日内每小时的能量流动结果,获得每日最大收益,目标函数可以表示为
1.3约束条件
2.改进粒子群算法求解
经典粒子群算法是一种基于群体智能的全局随机搜索算法[17-18],通用性较强,在各个工程领域中都得到广泛的应用。但经典粒子群算法在解决复杂高维优化问题时,容易陷入局部极值且收敛速度减慢[19]。因此,本文提出一种改进粒子群算法,对惯性权重、学习因子、速度限制等参数进行自适应调整,优化粒子个体的寻优能力。同时施加速度变异,保障求解结果为全局最优解。改进的粒子群算法流程如图 2 所示。
3)惯性权重取值将影响整个过程的收敛性与优化结果。对于当前适应度较大的粒子,其惯性权重因子应较小,从而在群体中保留该微粒,反之则应设置较大的惯性权重。因此,对惯性权重因子的取值做出调整,一方面使整体惯性权重随迭代次数线性递减,另一方面根据当前各粒子适应度差异性,自适应调节单个粒子的惯性权重。这种惯性权重修正方式可表示为
3.编程思路分析
3.1参数和变量定义
表1 相关参数
表2 上层决策变量
| 变量 |
Matlab定义 |
含义 |
维度 |
|
|
A_PV |
光伏板面积 |
1 |
|
|
E_b |
储能额定容量 |
1 |
表3 下层决策变量
3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。算例分析用到的大部分数据可以从原文中找到,其他数据可以自己假设一下。然后将所有需要的数据,按照表1的定义格式输入即可。
步骤2:上层备选集
上层优化中决策变量是光伏板的容量和储能容量,但实际上还需要由光伏板的容量、太阳辐射强度以及其他相关参数计算出光伏的输出功率。在一个确定的时间,太阳辐射强度是固定的,其他参数也都是固定的,因此可以认为光伏输出功率和光伏容量是线性关系,我在代码中表示为:
因为文中算例分析中以及给出了光伏容量的最优配置为30m²,同时也提供了该情况下光伏的出力曲线,所以令每小时光伏出力÷30,就可以得到系数取值。
步骤3:内层模型中决策变量的设置
元文中提到,内层模型中决策变量为储能荷电状态Sb,而其他的变量都可以通过计算得到,具体如下:
步骤4:粒子群算法的实现
原文中所谓的改进粒子群算法和普通的粒子群算法没有多大区别,加入的5点改进,改进1其实就是把问题的精度降低,以使搜索空间减小,改进2-5是一些比较常规的做法,改进6就是初始化的时候,和问题的背景相结合,具体实现方式如下:
①粒子的初始化
文献中的模型比较简单,决策变量初始化时,起始时段和末尾时段都是固定值0.5,所谓写了线性增加,线性减小的地方都是固定值,真正随机的只有写了Random的地方。
②适应度函数的计算
有点无法理解文中公式4所表达的含义,当P_grid大于0时,表示需要向电网购电,那么购电费用就是P_grid×对应的分时电价。但文中将(负荷—向电网购电量)×分时电价称之为电价收益,有点不太理解,这一项最多只能说是通过配置光伏和储能,减少的购电费用,但减少了就能说是收益嘛?而且为什么只把减少的量放进来,不拿购电量放进来。反正我是没有理解这部分的逻辑,但可能是有哪些地方我没有参透吧,代码中我还是按照他给的方式来写的。
粒子群算法中对于约束条件的处理有很多种形式,我在代码中参考这篇文章给的罚函数法进行处理:粒子群算法求解带约束优化问题 - 知乎
③每次迭代时更新速度上下限,惯性权重以及学习因子。
④加入变异机制
步骤5:输出运行结果
参考文中的图表的格式,输出结果即可。
4.Matlab代码
%% 清除内存空间
clc
clear
close all
%% 通过遍历光伏和储能的备选集合求最优配置方案
parameters;
it_num = length(20:5:160)*length(0.5:0.5:20);
I_INlayer = zeros(1,it_num);
S_b_INlayer = zeros(it_num,25);
I_CCER = zeros(1,it_num);
C_PV = zeros(1,it_num);
N_y = 365;
I_outlayer = zeros(1,it_num);
A_PVi = zeros(1,it_num);
E_bi = zeros(1,it_num);
it = 1;
for A_PV = 20:5:160
for E_b = 0.5:0.5:20
A_PVi(it) = A_PV;
E_bi(it) = E_b;
[I_INlayer(it) , S_b_INlayer(it,:)] = PSO_main(A_PV , E_b);
I_CCER(it) = sum(A_PV*S_PV*N_y*lambda_e);
C_PV(it) = A_PV*(N_PO*x_PC/sum((1 + rs).^(0:20)) + x_PC);
I_outlayer(it) = C_PV(it)/(I_CCER(it) + N_y*I_INlayer(it));
if I_outlayer(it) > 0
disp(['当光伏板面积=',num2str(A_PV),'㎡,储能容量=',num2str(E_b),'kW·h时,日收益最大为',...
num2str(I_INlayer(it)),'元,投资回收期为' , num2str(I_outlayer(it)) ,'年'])
else
disp(['当光伏板面积=',num2str(A_PV),'㎡,储能容量=',num2str(E_b),'kW·h时,日收益最大为',...
num2str(I_INlayer(it)),'元,无法回收成本'])
end
it = it + 1;
end
end
%% 输出结果
I_outlayer(I_outlayer < 0) = inf;
show_result;以上仅为主函数部分的matlab代码,完整的matlab代码可以从这个链接获取:
https://download.csdn.net/download/weixin_44209907/88178958
5.运行结果分析
因为原文并未提供完整的数据,因此结果不完全一样,但原理是相同的