Leetcode周赛 | 2023-8-6
2023-8-6
- 题1
-
- 体会
- 我的代码
- 题2
-
- 我的超时代码
- 题目
- 体会
- 我的代码
- 题3
-
- 体会
- 我的代码
题1
体会
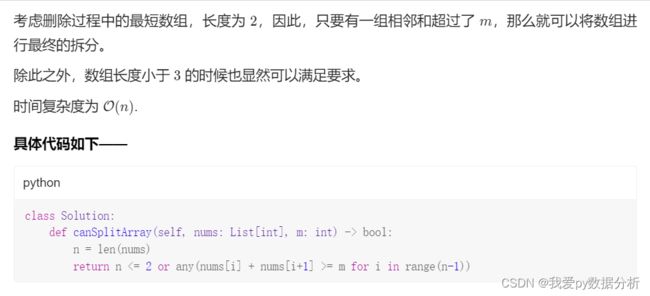
这道题完全就是唬人,只要想明白了,只要有两个连续的数的和,大于target,那么一定可以,两边一次切一个就好了。
我的代码
题2
我的超时代码
尽力了,想不出来别的方法,只能通过一半的测试用例,其他超时。
将向左和向下的代码去掉后,因为我觉得向左和向右是无意义的,通过的用例多了一些,但还是超时。
class Solution:
def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
note = []
m = len(grid)
n = len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1 :
note.append([i,j])
if i == 0 and j == 0 :
return 0
if i == m-1 and j == n-1 :
return 0
self.mm = 0
i = j = 0
mini = inf
self.dfs(grid,i,j,mini,note,m,n)
return self.mm
def dfs(self,grid,i,j,mini,note,m,n):
if i < 0 or i >= m or j < 0 or j >= n :
return
if grid[i][j] == 2 :
return
temp = [[p[0]-i,p[1]-j] for p in note]
for k in temp :
mini = min(mini,abs(k[0])+abs(k[1]))
if mini <= self.mm :
return
if i == m-1 and j == n-1 :
self.mm = max(self.mm,mini)
return
grid[i][j] = 2
self.dfs(grid,i+1,j,mini,note,m,n)
self.dfs(grid,i-1,j,mini,note,m,n)
self.dfs(grid,i,j+1,mini,note,m,n)
self.dfs(grid,i,j-1,mini,note,m,n)
grid[i][j] = 0
改成了动态规划的方法,还是解答错误,但是通过的用例更多了
(983 / 1035)
class Solution:
def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
note = []
m = len(grid)
n = len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1 :
note.append([i,j])
if i == 0 and j == 0 :
return 0
if i == m-1 and j == n-1 :
return 0
dp = [[0]*(n) for _ in range(m)]
for i in range(0,m):
for j in range(0,n):
mini = inf
temp = [[p[0]-(i),p[1]-(j)] for p in note]
for k in temp :
mini = min(mini,abs(k[0])+abs(k[1]))
'''
if mini < dp[i-1][j] and mini < dp[i][j-1] :
dp[i][j] = mini
elif mini > dp[i-1][j] and mini > dp[i][j-1] :
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
else :
dp[i][j] = mini
'''
if i == 0 and j != 0:
kk = dp[i][j-1]
elif j == 0 and i!=0:
kk = dp[i-1][j]
elif j == 0 and i==0:
kk = inf
else :
kk = max(dp[i-1][j],dp[i][j-1])
if mini < kk :
dp[i][j] = mini
else :
dp[i][j] = kk
#return dp
return dp[-1][-1]
两次动归也不对。
class Solution:
def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
note = []
m = len(grid)
n = len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1 :
note.append([i,j])
if i == 0 and j == 0 :
return 0
if i == m-1 and j == n-1 :
return 0
dp = [[0]*(n) for _ in range(m)]
for i in range(0,m):
for j in range(0,n):
mini = inf
temp = [[p[0]-(i),p[1]-(j)] for p in note]
for k in temp :
mini = min(mini,abs(k[0])+abs(k[1]))
'''
if mini < dp[i-1][j] and mini < dp[i][j-1] :
dp[i][j] = mini
elif mini > dp[i-1][j] and mini > dp[i][j-1] :
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
else :
dp[i][j] = mini
'''
if i == 0 and j != 0:
kk = dp[i][j-1]
elif j == 0 and i!=0:
kk = dp[i-1][j]
elif j == 0 and i==0:
kk = inf
else :
kk = max(dp[i-1][j],dp[i][j-1])
if mini < kk :
dp[i][j] = mini
else :
dp[i][j] = kk
dp2 = [[0]*(n) for _ in range(m)]
for i in range(m-1,-1,-1):
for j in range(n-1,-1,-1):
mini = inf
temp = [[p[0]-(i),p[1]-(j)] for p in note]
for k in temp :
mini = min(mini,abs(k[0])+abs(k[1]))
'''
if mini < dp[i-1][j] and mini < dp[i][j-1] :
dp[i][j] = mini
elif mini > dp[i-1][j] and mini > dp[i][j-1] :
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
else :
dp[i][j] = mini
'''
if i == m-1 and j != n-1:
kk = dp[i][j+1]
elif j == n-1 and i!=m-1:
kk = dp[i+1][j]
elif j == n-1 and i==m-1:
kk = inf
else :
kk = max(dp[i+1][j],dp[i][j+1])
if mini < kk :
dp[i][j] = mini
else :
dp[i][j] = kk
#return dp
return max(dp[-1][-1],dp2[-1][-1])
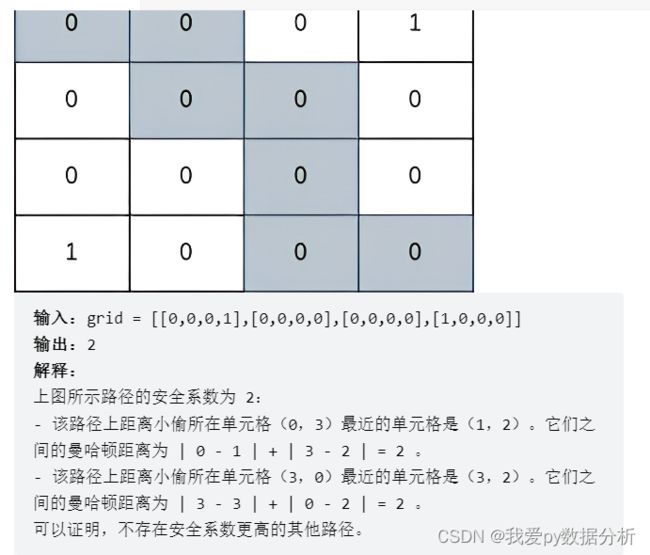
题目
体会
因为不仅可以向右和向下走,还可以向上和向左,所以不能dp。
从来没接触过这道题的解法,也看不懂。
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
def find(self, a):
a = self.parent[a]
acopy = a
while a != self.parent[a]:
a = self.parent[a]
while acopy != a:
self.parent[acopy], acopy = a, self.parent[acopy]
return a
def merge(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb: return False
self.parent[pb] = pa
return True
class Solution:
def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
n = len(grid)
dist = [[inf] * n for _ in range(n)]
tmp = deque([(i, j) for i in range(n) for j in range(n) if grid[i][j]])
for i, j in tmp:
dist[i][j] = 0
while tmp:
i, j = tmp.popleft()
for dx, dy in pairwise([-1, 0, 1, 0, -1]):
if 0 <= i + dx < n and 0 <= j + dy < n and dist[i+dx][j+dy] == inf:
dist[i+dx][j+dy] = dist[i][j] + 1
tmp.append((i+dx, j+dy))
l, r = 0, 2 * n - 2
while l <= r:
m = (l + r) // 2
union = UnionFind(n * n)
for i in range(n):
for j in range(n):
if dist[i][j] >= m:
if i < n - 1 and dist[i+1][j] >= m: union.merge(i * n + j, (i + 1) * n + j)
if j < n - 1 and dist[i][j+1] >= m: union.merge(i * n + j, i * n + j + 1)
if union.find(0) == union.find(n * n - 1): l = m + 1
else: r = m - 1
return r
我的代码
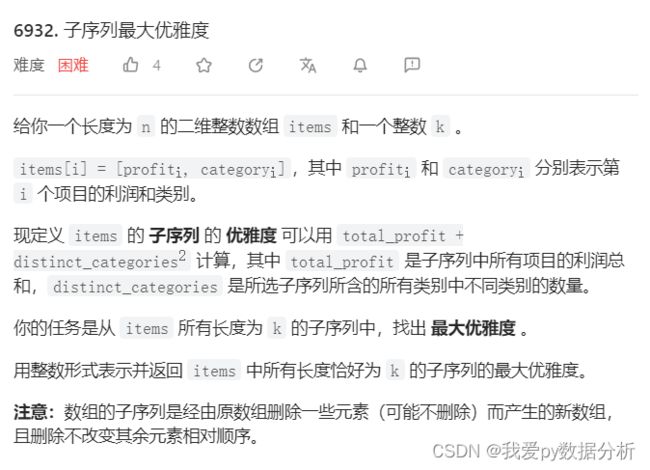
题3
体会
class Solution:
def findMaximumElegance(self, items: List[List[int]], k: int) -> int:
items.sort(reverse=True)
chosen = set()
to_delete = []
tot = 0
for i in range(k):
x, t = items[i]
tot += x
if t in chosen: heappush(to_delete, x)
else: chosen.add(t)
ans = tot + len(chosen) ** 2
for i in range(k, len(items)):
x, t = items[i]
if t not in chosen and len(to_delete):
chosen.add(t)
tot -= heappop(to_delete)
tot += x
ans = max(ans, tot + len(chosen) ** 2)
return ans