vue diff 前后缀+最长递增子序列算法

查找相同前后缀

• 如上图所示，新旧 children 拥有相同的前缀节点和后缀节点
• 对于前缀节点，我们可以建立一个索引，指向新旧 children 中的第一个节点，并逐步向后遍历，直到遇到两个拥有不同 key 值的节点为止

// 更新相同的前缀节点
// j 为指向新旧 children 中第一个节点的索引
let j = 0
let prevVNode = prevChildren[j]
let nextVNode = nextChildren[j]
// while 循环向后遍历，直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
  // 调用 patch 函数更新
  patch(prevVNode, nextVNode, container)
  j++
  prevVNode = prevChildren[j]
  nextVNode = nextChildren[j]
}

• 对于相同的后缀节点，由于新旧 children 中节点的数量可能不同，所以我们需要两个索引分别指向新旧 children 的最后一个节点，并逐步向前遍历，直到遇到两个拥有不同 key 值的节点为止

// 更新相同的后缀节点

// 指向旧 children 最后一个节点的索引
let prevEnd = prevChildren.length - 1
// 指向新 children 最后一个节点的索引
let nextEnd = nextChildren.length - 1

prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]

// while 循环向前遍历，直到遇到拥有不同 key 值的节点为止
while (prevVNode.key === nextVNode.key) {
  // 调用 patch 函数更新
  patch(prevVNode, nextVNode, container)
  prevEnd--
  nextEnd--
  prevVNode = prevChildren[prevEnd]
  nextVNode = nextChildren[nextEnd]
}

通过前后缀位置信息新增节点

// 前缀节点终止位置
j: 1
// 后缀节点终止位置
prevEnd: 0
nextEnd: 1

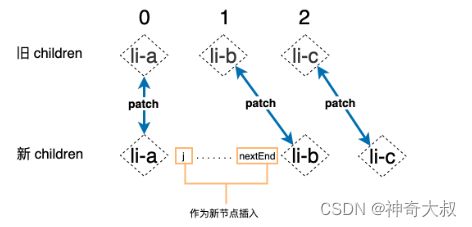
• 发现 j > prevEnd 并且 j <= nextEnd，这说明当新旧 children 中相同的前缀和后缀被更新之后，旧 children 中的节点已经被更新完毕了，而新 children 中仍然有剩余节点，通过上图可以发现，新 children 中的 li-d 节点，就是这个剩余的节点。实际上新 children 中位于 j 到 nextEnd 之间的所有节点都应该是新插入的节点：
  

// 满足条件，则说明从 j -> nextEnd 之间的节点应作为新节点插入
if (j > prevEnd && j <= nextEnd) {
  // 所有新节点应该插入到位于 nextPos 位置的节点的前面
  const nextPos = nextEnd + 1
  const refNode =
    nextPos < nextChildren.length ? nextChildren[nextPos].el : null
  // 采用 while 循环，调用 mount 函数挂载节点
  while (j <= nextEnd) {
    mount(nextChildren[j++], container, false, refNode)
  }
}

通过前后缀位置信息删除节点

• 在这个案例中，当“去掉”相同的前缀和后缀之后，三个索引的值为：

j: 1
prevEnd: 1
nextEnd: 0

• 这时条件 j > nextEnd 并且 j <= prevEnd 成立，通过上图可以很容的发现，旧 children 中的 li-b 节点应该被移除，实际上更加通用的规则应该是：在旧 children 中有位于索引 j 到 prevEnd 之间的节点，都应该被移除

if (j > prevEnd && j <= nextEnd) {
  // j -> nextEnd 之间的节点应该被添加
  const nextPos = nextEnd + 1
  const refNode =
    nextPos < nextChildren.length ? nextChildren[nextPos].el : null
  while (j <= nextEnd) {
    mount(nextChildren[j++], container, false, refNode)
  }
} else if (j > nextEnd) {
  // j -> prevEnd 之间的节点应该被移除
  while (j <= prevEnd) {
    container.removeChild(prevChildren[j++].el)
  }
}

• 假设在第一个 while 循环结束之后，索引 j 的值已经大于 prevEnd 或 nextEnd，那么还有必须执行第二个 while 循环吗？答案是没有必要，这是因为一旦索引 j 大于 prevEnd 则说明旧 children 中的所有节点都已经参与了 patch，类似的，如果索引 j 大于 nextEnd 则说明新 children 中的所有节点都已经参与了 patch，这时当然没有必要再执行后续的操作了。

while (prevVNode.key === nextVNode.key) {
  patch(prevVNode, nextVNode, container)
  j++
  if (j > prevEnd || j > nextEnd) {
    break;
  }
  prevVNode = prevChildren[j]
  nextVNode = nextChildren[j]
}
// 更新相同的后缀节点
prevVNode = prevChildren[prevEnd]
nextVNode = nextChildren[nextEnd]
while (prevVNode.key === nextVNode.key) {
  patch(prevVNode, nextVNode, container)
  prevEnd--
  nextEnd--
  if (j > prevEnd || j > nextEnd) {
    break outer
  }
  prevVNode = prevChildren[prevEnd]
  nextVNode = nextChildren[nextEnd]
}

if(!(j > prevEnd && j>prevEnd)){
	// 满足条件，则说明从 j -> nextEnd 之间的节点应作为新节点插入
	if (j > prevEnd && j <= nextEnd) {
	  // j -> nextEnd 之间的节点应该被添加
	  // 省略...
	} else if (j > nextEnd) {
	  // j -> prevEnd 之间的节点应该被移除
	  // 省略...
	}
}
 

中间部份 diff

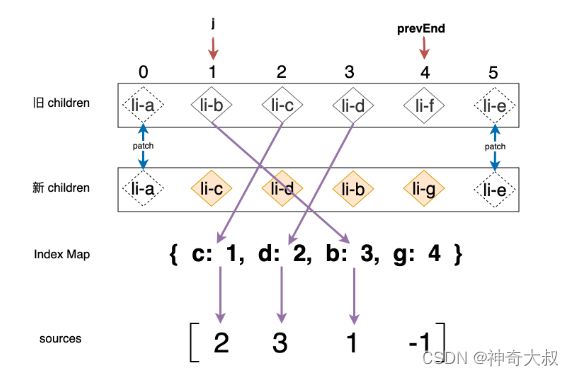
• 首先，我们需要构造一个数组 source，该数组的长度等于新 children 在经过预处理之后剩余未处理节点的数量，初始化该数组中每个元素的初始值为 -1
• 实际上 source 数组将用来存储新 children 中的节点在旧 children 中的位置，后面将会使用它计算出一个最长递增子序列，并用于 DOM 移动
  
• 再建立一个 Index Map 中的键是节点的 key，值是节点在新 children 中的位置索引，用空间来换取时间上的优化
  

if (j > prevEnd && j <= nextEnd) {
  // 省略...
} else if (j > nextEnd) {
  // 省略...
} else {
	// 构造 source 数组
	const nextLeft = nextEnd - j + 1  // 新 children 中剩余未处理节点的数量
	const source = []
	for (let i = 0; i < nextLeft; i++) {
	  source.push(-1)
	}
	
	const prevStart = j
	const nextStart = j
	let moved = false
	let pos = 0
	// 构建索引表
	const keyIndex = {}
	for(let i = nextStart; i <= nextEnd; i++) {
	  keyIndex[nextChildren[i].key] = i
	}
	// 遍历旧 children 的剩余未处理节点
	for(let i = prevStart; i <= prevEnd; i++) {
	  prevVNode = prevChildren[i]
	  // 通过索引表快速找到新 children 中具有相同 key 的节点的位置
	  const k = keyIndex[prevVNode.key]
	
	  if (typeof k !== 'undefined') {
	    nextVNode = nextChildren[k]
	    // patch 更新
	    patch(prevVNode, nextVNode, container)
	    // 更新 source 数组
	    source[k - nextStart] = i
	    // 判断是否需要移动
	    if (k < pos) {
	      moved = true
	    } else {
	      pos = k
	    }
	  } else {
	    // 没找到
	  }
	}

}

判断节点是否需要移动

• 在上一步代码中，遍历旧 children 的剩余未处理节点，通过索引表快速找到新 children 中具有相同 key 的节点的位置
• 如果新旧节点位置没有变化，那么位置信息应该是相同的，否则，新节点索引表信息为[1,2,3,4]，如果映射成旧节点为[1,2,4,3]，说明旧节点的最后一个位置和前面的位置互换了，说明节点移动了

const prevStart = j
const nextStart = j
let moved = false
let pos = 0
// 构建索引表
const keyIndex = {}
for(let i = nextStart; i <= nextEnd; i++) {
  keyIndex[nextChildren[i].key] = i
}
// 遍历旧 children 的剩余未处理节点
for(let i = prevStart; i <= prevEnd; i++) {
  prevVNode = prevChildren[i]
  // 通过索引表快速找到新 children 中具有相同 key 的节点的位置
  const k = keyIndex[prevVNode.key]

  if (typeof k !== 'undefined') {
    nextVNode = nextChildren[k]
    // patch 更新
    patch(prevVNode, nextVNode, container)
    // 更新 source 数组
    source[k - nextStart] = i
    // 判断是否需要移动
    if (k < pos) {
      moved = true
    } else {
      pos = k
    }
  } else {
    // 没找到
  }
}

删除节点

删除未查找到的节点

• 拿旧 children 中的节点尝试去新 children 中寻找具有相同 key 值的节点，但并非总是能够找得到，当 k === ‘undefined’ 时，说明该节点在新 children 中已经不存在了，这时我们应该将其移除

// 遍历旧 children 的剩余未处理节点
for(let i = prevStart; i <= prevEnd; i++) {
  prevVNode = prevChildren[i]
  // 通过索引表快速找到新 children 中具有相同 key 的节点的位置
  const k = keyIndex[prevVNode.key]

  if (typeof k !== 'undefined') {
    // 省略...
  } else {
    // 没找到，说明旧节点在新 children 中已经不存在了，应该移除
    container.removeChild(prevVNode.el)
  }
}

删除多余节点

• 旧 children 中已经更新过的节点数量应该小于新 children 中需要更新的节点数量，一旦更新过的节点数量超过了新 children 中需要更新的节点数量，则说明该节点是多余的节点，我们也应该将其移除

const nextLeft = nextEnd - j + 1  // 新 children 中剩余未处理节点的数量
let patched = 0
// 遍历旧 children 的剩余未处理节点
for (let i = prevStart; i <= prevEnd; i++) {
  prevVNode = prevChildren[i]

  if (patched < nextLeft) {
    // 通过索引表快速找到新 children 中具有相同 key 的节点的位置
    const k = keyIndex[prevVNode.key]
    if (typeof k !== 'undefined') {
      nextVNode = nextChildren[k]
      // patch 更新
      patch(prevVNode, nextVNode, container)
      patched++
      // 更新 source 数组
      source[k - nextStart] = i
      // 判断是否需要移动
      if (k < pos) {
        moved = true
      } else {
        pos = k
      }
    } else {
      // 没找到，说明旧节点在新 children 中已经不存在了，应该移除
      container.removeChild(prevVNode.el)
    }
  } else {
    // 多余的节点，应该移除
    container.removeChild(prevVNode.el)
  }
}

移动和新增节点

最长递增子序列

• source 数组的值为 [2, 3, 1, -1]，很显然最长递增子序列应该是 [ 2, 3 ]，换算成位置信息是 [ 0, 1 ]
• 而最长递增子序列是 [ 0, 1 ] 这告诉我们：新 children 的剩余未处理节点中，位于位置 0 和位置 1 的节点的先后关系与他们在旧 children 中的先后关系相同。或者我们可以理解为位于位置 0 和位置 1 的节点是不需要被移动的节点
• 只有 li-b 节点和 li-g 节点是可能被移动的节点，但是我们发现与 li-g 节点位置对应的 source 数组元素的值为 -1，这说明 li-g 节点应该作为全新的节点被挂载，所以只有 li-b 节点需要被移动
• 使用 for 循环从后向前遍历新 children 中剩余未处理的子节点
• 这里的技巧在于 i 的值的范围是 0 到 nextLeft - 1，这实际上就等价于我们对剩余节点进行了重新编号。接着判断当前节点的位置索引值 i 是否与子序列中位于 j 位置的值相等，如果不相等，则说明该节点需要被移动；如果相等则说明该节点不需要被移动，并且会让 j 指向下一个位置
• 节点需要被怎么移动呢？找到 li-b 节点的后一个节点(li-g)，将其插入到 li-g 节点的前面即可

if (moved || source.indexOf(-1)!==-1) {
  // 根据 source 数组计算一个最长递增子序列：
  const seq = lis(sources) // [ 0, 1 ],代表的是最长递增子序列中的各个元素在 source 数组中的位置索引
  let j = seq.length - 1
  // 从后向前遍历新 children 中的剩余未处理节点
  for (let i = nextLeft - 1; i >= 0; i--) {
    if (source[i] === -1) {
      // 作为全新的节点挂载

      // 该节点在新 children 中的真实位置索引
      const pos = i + nextStart
      const nextVNode = nextChildren[pos]
      // 该节点下一个节点的位置索引
      const nextPos = pos + 1
      // 挂载
      mount(
        nextVNode,
        container,
        false,
        nextPos < nextChildren.length
          ? nextChildren[nextPos].el
          : null
      )
    } else if (i !== seq[j]) {
      // 说明该节点需要移动
      // 该节点在新 children 中的真实位置索引
      const pos = i + nextStart
      const nextVNode = nextChildren[pos]
      // 该节点下一个节点的位置索引
      const nextPos = pos + 1
      // 移动
      container.insertBefore(
        nextVNode.el,
        nextPos < nextChildren.length
          ? nextChildren[nextPos].el
          : null
      )
    } else {
      // 当 i === seq[j] 时，说明该位置的节点不需要移动
      // 并让 j 指向下一个位置
      j--
    }
  }
}

}

求解最长递增子序列位置信息

[ 0, 8, 4, 12, 2, 10]
// 最长递增子序列长度
[ 3, 2, 2, 1, 2, 1]

• 如上可知最长子序列长度为 3，从右往左遍历查找子序列长度为2位置，接着查找为1的位置，这样就能找到所有的位置信息

// 所有的最长递增子序列
[ 0, 8, 12 ]
[ 0, 8, 10 ]
[ 0, 4, 12 ]
[ 0, 4, 10 ]
[ 0, 2, 10 ]