Day5：Googlenet网络理解

一、Googlenet简介

GoogLeNet是2014年Christian Szegedy提出的一种全新的深度学习结构，在这之前的AlexNet、VGG等结构都是通过增大网络的深度（层数）来获得更好的训练效果，但层数的增加会带来很多负作用，比如overfit、梯度消失、梯度爆炸等。inception的提出则从另一种角度来提升训练结果：能更高效的利用计算资源，在相同的计算量下能提取到更多的特征，从而提升训练结果。

二、Googlenet创新点

【通过增加网络深度和宽度来获得高质量模型存在的两个问题：一是更大的网络规模往往意味着更多的参数，这使得扩大后的网络更易过拟合。二是统一增加网络大小的缺陷是计算资源需求的暴增。】

（一）inception

1、背景：通过增大网络深度和宽度带来以上两个问题，为解决以上两个问题就是在增加深度和宽度的同时减少参数，这就需要全连接就需要变成稀疏连接，但是，全连接变成稀疏连接后的计算实际是很低效的，因为大部分硬件是针对密集矩阵计算优化的，稀疏矩阵虽然数据量少，但是所耗的时间却是很难缺少。因此，提出了inception，它的体系结构的主要设计思路是要在一个卷积视觉网络中寻找一个局部最优的稀疏结构，同时这个结构需要能够被可获得的密集组件（dense component）覆盖和近似表达。【总结：为了获得高质量模型→加深模型→参数增多→全连接变稀疏连接→计算并不会提升→提出inception（既稀疏又提高计算机性能）】

2、inception结构

Inception结构的主要思想是怎样用密集成分来近似最优的局部稀疏结构

（a） 将一张图片输入，采用1*1、3*3、5*5不同大小的卷积核分别来提取特征，最后将卷积核池化后的特征图像进行concat（在不同的卷积核卷积时进行了不同大小的padding），采用不同大小的卷积核意味着不同大小的感受野（当目标对象在图片较深的位置采用小卷积核学习，反之采用大卷积核学习），最后拼接意味着不同尺度特征的融合。

（b）使用5x5的卷积核仍然会带来巨大的计算量。 为此，论文借鉴NIN结构，采用1x1卷积核来进行降维。 从而可以降低concat后feature map的厚度。

（二）2个辅助的softmax

1、背景：对于相对更深的网络，穿过所有层次高效向后梯度传播的能力是很关键的。当加深网络后，会出现梯度回传消失的现象，因此提出在网络中间层增加两个辅助的分类器。

2、辅助的softmax

通过增加一些与这些中间层相连的附加的分类器，我们可以期待在分类器的低层增加向后传播的梯度信号，同时增加更多的正则化。这些分类器采用较小的卷积网络形式，被安置在Inception（4a）和（4d）模块的输出的顶部。在训练中，它们的偏差被折扣后加到总偏差中（附加分类器的偏差乘以0.3）。在预测过程中，这些附加网络会被抛弃。

 

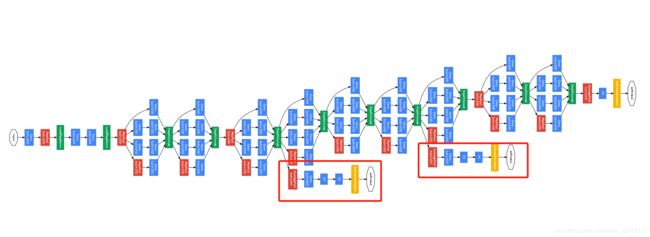
三、网络简介

网络结构如上图所示，共22层（ 只计算有参数的层，GoogleNet网络有22层深 ，算上池化层有27层），原始数据输入大小为224 * 224 * 3。

具体每层不做具体分析，其参数如下：

 分析一下第一个inception:

 

输入28 * 28 * 192 进行split 分成四个支线：

1： 64个1 * 1的卷积核降维变成28 * 28 * 64， 进行relu计算后

2：先经96个1 * 1的卷积核降维变成28 * 28 * 96， 进行relu计算后，再进行128个3 * 3的卷积，pad为1，变成28 * 28 * 128

3：先经16个1 * 1的卷积核降维变成28 * 28 * 16， 进行relu计算后，再进行32个5 * 5的卷积，

pad为2，变成28 * 28 * 32

4：先经pool层，3 * 3的核，pad为1，输出还是28 * 28 * 192，再进行32个 1 * 1的卷积，变成 28 * 28 * 32

最后将四个分支的feature map concat便成为28 * 28 * 256。

四、Pytorch代码实现

Inception实现

import torch
from torch import nn, optim
import torch.nn.functional as F
class Inception(nn.Module):
    # c1 - c4为每条线路里的层的输出通道数
    def __init__(self, in_c, c1, c2, c3, c4):
        super(Inception, self).__init__()
        # 线路1，单1 x 1卷积层
        self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3 x 3最大池化层后接1 x 1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
 
    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1)  # 在通道维上连结输出

GlobalAvgPool2d与FlattenLayer

class GlobalAvgPool2d(nn.Module):
    # 全局平均池化层可通过将池化窗口形状设置成输入的高和宽实现
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    def forward(self, x):
        return F.avg_pool2d(x, kernel_size=x.size()[2:])
    
class FlattenLayer(torch.nn.Module):
    def __init__(self):
        super(FlattenLayer, self).__init__()
    def forward(self, x): # x shape: (batch, *, *, ...)
        return x.view(x.shape[0], -1)

GoogLeNet实现

class GoogLeNet(nn.Module):
    def __init__(self, num_classes=1000):
        super(GoogLeNet, self).__init__()
        
        self.b1 = nn.Sequential(nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3),
                           nn.ReLU(),
                           nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

        self.b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                           nn.Conv2d(64, 192, kernel_size=3, padding=1),
                           nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

        self.b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                           Inception(256, 128, (128, 192), (32, 96), 64),
                           nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

        self.b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                           Inception(512, 160, (112, 224), (24, 64), 64),
                           Inception(512, 128, (128, 256), (24, 64), 64),
                           Inception(512, 112, (144, 288), (32, 64), 64),
                           Inception(528, 256, (160, 320), (32, 128), 128),
                           nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

        self.b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                           Inception(832, 384, (192, 384), (48, 128), 128),
                           GlobalAvgPool2d())
        self.output=nn.Sequential(FlattenLayer(),
                                  nn.Dropout(p=0.4),
                                  nn.Linear(1024, 1000))
        
        def forward(self, x):
            x=b1(x)
            x=b2(x)
            x=b3(x)
            x=b4(x)
            x=b5(x)
            x=output(x)
            return x

参考：

https://blog.csdn.net/qq_37555071/article/details/108214680

https://blog.csdn.net/abc_138/article/details/80412413