【蓝桥杯2022初赛题解】Python

剪指刀

题目描述

小蓝有一个裁纸刀，每次可以将一张纸沿一条直线裁成两半。
小蓝用一张纸打印出两行三列共 6 个二维码，至少使用九次裁出来，下图给出了一种裁法。

在上面的例子中，小蓝的打印机没办法打印到边缘，所以边缘至少要裁4次。
另外，小蓝每次只能裁一张纸，不能重叠或者拼起来裁。
如果小蓝要用一张纸打印出 20 行 22 列共 440 个二维码，他至少需要裁多少次？
答案：443

代码

'''
设行为n，列为m，由题目中的裁法知：
行上面需要裁剪n + 1次，列上面(m - 1) * n + 2
'''

n, m = 20, 22
print(n + 1 + (m - 1) * n + 2)

寻找整数 【剩余定理】

题目描述

有一个不超过10^17的正整数n，知道这个数除以2至49后的余数如下表所示，求这个正整数最小是多少。

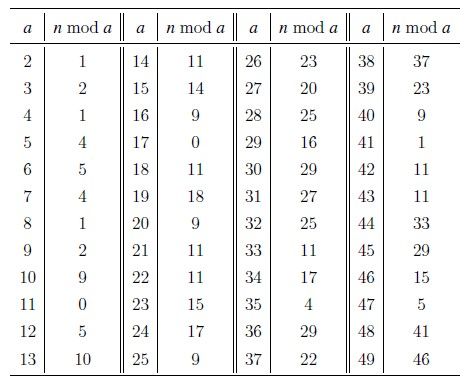
这是一道结果填空的题，你只需要算出结果后提交即可。
本题的结果为一个整数，在提交答案时输出这个整数，输出多余的内容将无法得分。
答案：2022040920220409

思路

题目是让我们求一个整数n(n < 10 ** 17)，n满足除以2~49得到的相应余数。
这里参考了一位博主的做法，清晰易懂：
首先假设x满足 x % m1 = a1, x % m2 = a2, 下一个x满足 x + lcm(m1, m2), 举个栗子
x = 7, m1=2, m2=3, 那么下一个x = 7 + lcm(2, 3) = 13 这里lcm是求最小公倍数

以m1为基准如果x % m1 满足条件，先更新lcm=lcm(lcm, m1)，再更新m1
如果不满足条件直到找到满足条件的x为止 x += lcm

代码中x就是ans，m1就是id。

代码

'''
from math import gcd

d = [0, 0, 1, 2, 1, 4, 5, 4, 1, 2, 9,
     0, 5, 10, 11, 14, 9, 0, 11, 18, 9,
     11, 11, 15, 17, 9, 23, 20, 25, 16, 29,
     27, 25, 11, 17, 4, 29, 22, 37, 23, 9,
     1, 11, 11, 33, 29, 15, 5, 41, 46]

id = 2
ans = lcm = 0
while id <= 49:
    if id == 2:
        lcm, ans = id, d[id]
    if ans % id == d[id]:
        lcm = lcm * id // gcd(lcm, id)
        id += 1
    else:
        ans += lcm

print(ans)

矩阵拼接 【模拟】

题目描述

思路

具体细节看代码。

代码

def cal(a1, b1, a2, b2, a3, b3):
    x = [[a1, b1], [a2, b2], [a3, b3]]
    x.sort(reverse=True)
    a1, b1, a2, b2, a3, b3 = x[0][0], x[0][1], x[1][0], x[1][1], x[2][0], x[2][1]
    if a1 == a2 and a2 == a3:
        return 4
    if a1 == a2 or a2 == a3:
        return 6
    if a1 == a2 + a3:
        if b2 == b3:
            return 4
        else:
            return 6
    if b1 == b2 or b2 == b3:
        return 6
    return 8


t = int(input())
for _ in range(t):
    x = list(map(int, input().split()))
    ans = 8
    for i in range(2):
        a1 = x[i]
        b1 = x[1 - i]
        for j in range(2, 4):
            a2 = x[j]
            b2 = x[5 - j]
            for k in range(4, 6):
                a3 = x[k]
                b3 = x[9 - k]
                ans = min(ans, cal(a1, b1, a2, b2, a3, b3))
    print(ans)

质因素个数 【质因素分解】

题目描述

给定正整数n，请问有多少个质数是n的约数。

思路

筛选出所有的质因素，将396分解成2 * 2 * 3 * 3 * 11。

代码

n = int(input())
cnt = 0
i = 2
while i * i <= n:
    if n % i == 0:
        cnt += 1
        while n % i == 0:
            n //= i
    i += 1
if n > 1:
    cnt += 1
print(cnt)

技能升级 【二分】

题目描述

小蓝最近正在玩一款RPG 游戏。他的角色一共有N个可以加攻击力的技能。
其中第i个技能首次升级可以提升Ai点攻击力，以后每次升级增加的点数都会减少Bi。
⌈Ai/Bi⌉ (向上取整) 次之后，再升级该技能将不会改变攻击力。
现在小蓝可以总计升级M次技能，他可以任意选择升级的技能和次数。
请你计算小蓝最多可以提高多少点攻击力？

思路1(50分)【优先队列】

利用优先队列来模拟每次升级的操作。

代码

import heapq as hq
n, m = map(int, input().split())
queue = []
for _ in range(n):
    a, b = map(int, input().split())
    queue.append([-a, b])
 
ans = 0
hq.heapify(queue)
while m:
    # print(queue)
    m -= 1
    a, b = hq.heappop(queue)
    ans += -a
    if -a - b >= b:
        hq.heappush(queue, [a + b, b])
print(ans)

思路2(100分)【二分】

二分所有的升级可能，例如本题例子：10,9,8,7,7,6,5,5,5,4,3,3,2,1,1
设f(t) = m，表示大于等于t的个数为m，当x=f(y), 而f(x)>=m,时，x-1也满足，但x+1不一定满足。满足二分的情况，二分去找满足的t，找到t，我们再用等差数列去求每个技能大于等于t的和。同时记录大于等于t的个数，如果超过m，则减去超过的攻击力。

代码

def check(x):
    cnt = 0
    for i in range(n):
        if arr[i][0] >= x:
            cnt += (arr[i][0] - x) // arr[i][1] + 1
    return cnt >= m


n, m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(n)]

# 二分满足的t，直到找到恰好是m个元素为止
l, r = 0,  10 ** 6 + 1
while l + 1 < r:
    mid = (l + r) >> 1
    if check(mid):
        l = mid
    else:
        r = mid

# 找到t过后，再去找每个序列中都大于等于t的元素，可能等于t的有多个，最后减去即可。
ans, cnt = 0, 0
for i in range(n):
    if arr[i][0] >= l:
        # 以首项为a[i]，公差为b[i]的等差数列
        c = (arr[i][0] - l) // arr[i][1] + 1
        end = arr[i][0] - (c - 1) * arr[i][1]
        ans += (arr[i][0] + end) * c // 2
        cnt += c
# 减去等于t的元素
ans -= (cnt - m) * l
print(ans)

因素平方和【分块+前缀和+逆元】

题目描述

记f(x)为x的所有因数的平方的和。例如：f(12)= 1^2 + 2^2 + 3^2 + 4^2 + 6^2 + 12^2。
定义g(n)=f(1)+f(2)+…+f(n)。
给定n, 求g(n)除以10^9 + 7 的余数。

思路

g(n) = ${\sum }_{i=1}^{n}f(i)$， 相当于求i²被加了几次。
[1, n]中是1的倍数有n//1个
[1, n]中是2的倍数有n//2个
[1, n]中是3的倍数有n//3个
。。。
[1, n]中是n的倍数有n//n个
于是g(n) = $1^2\ast (n//1)+2^2\ast (n//2)+...+n^2\ast (n//n)$
但是这样算的话还是O(n)的复杂度，而n最大是1e9，所以要TLE，可以思考
12//7, 12//8,…,12//12都等于1，于是将这些相等的数合并成一起计算。就用到了数论分块的思想。[l,r]区间满足n//l = n//(l+1) = … = n//r。于是这段区间的值为$(l^2+(l+1{)}^2+...+r^2)$ * n//l。而$(l^2+(l+1{)}^2+...+r^2)$可以通过前缀和来求。
${\sum }_{i=1}^n{i}^2=\frac{n(n+1)(2n+1)}{6}$

我们在求i²的前缀和时要注意用逆元来求，不能去除以6，因为分子在进行取mod运算过后不一定是6的倍数。

代码

# a * 6 % (10 ** 7) == 1

mod = 10 ** 9 + 7
inv6 = (mod + 1) // 6  # 6在1e9+7下的逆元
n = int(input())
res = 0  # 答案
r_sum = l_sum = 0
l = r = 1  # 块的左端点和右端点
while l <= n:
    r = n // (n // l)
    l_sum = r_sum
    r_sum = r * (r + 1) % mod * (2 * r + 1) % mod * inv6 % mod  # 这里就是在计算i²的前r项和
    cur_sum = (r_sum - l_sum + mod) % mod  # 由于是取余过后的结果所以r_sum不一定比l_sum大，所以要加上mod
    res = (res + (n // l) % mod * cur_sum % mod) % mod
    l = r + 1  # 更新为下一个块的左端点
print(res)

爬树的甲壳虫 【DP + 逆元】

题目描述

有一只甲壳虫想要爬上一颗高度为n 的树，它一开始位于树根，高度为0。
当它尝试从高度 i-1 爬到高度为i 的位置时有 Pi 的概率会掉回树根。
求它从树根爬到树顶时，经过的时间的期望值是多少。

思路

以下是参考一位博主的思路：（果然数学好的人直接推公式）
从高度0-1的期望：
有p1的几率掉落到根，有1 - p_1的几率爬到1层。
爬1次到达1层的期望：$1\ast （1-p_1）$
爬2次到达1层的期望：$2\ast （1-p_1）\ast p1$
爬3次到达1层的期望：$3\ast (1-p_1)\ast p_1^2$
…
爬n次到达1层的期望：$n\ast (1-p_1)\ast p_1^{(}n-1)$
…
即爬到1层的期望是$E(1)={\sum }_{i=0}i\ast (1-p_1)\ast p_1^{i-1}=(1-p_1)\ast {\sum }_{i=0}i\ast p_1^{i-1}$
令$F(x)={\sum }_{i=0}i\ast p_1^{i-1}={\sum }_{i=1}(p_1^i{)}^{{}^{\prime }}={\sum }_{i=0}(p_1^i{)}^{{}^{\prime }}=({\sum }_{i=0}{p}_1^i{)}^{{}^{\prime }}$
即$F(x)=(\frac{1-x^{\infty }}{1-x}{)}^{{}^{\prime }}$ 又因为0$F(x)=(\frac{1}{1-x}{)}^{{}^{\prime }}=\frac{1}{{(1-x)}^2}$（里面就是一个等差数列求和）
即$E(1)=(1-p_1)\ast F(p_1)=\frac{1}{1-p_1}$
那么从高度(n-1)到n的期望：
爬1次到达n层的期望：$(E(n-1)+1)\ast (1-p_n)$
爬2次到达n层的期望：$(2\ast E(n-1)+1)\ast (1-p_n)\ast p_n$
爬3次到达n层的期望：$(3\ast E(n-1)+1)\ast (1-p_n)\ast p_n^2$
…
同理$E(n)=(E(n-1)+1)\ast \frac{1}{1-p_n}$
即$E(n)=(E(n01)+1)\ast \frac{y_i}{y_i-x_i}$
由于除以$y_i-x_i$要失精度，所以用逆元去乘以${y_i-x_i}^{-1}$，逆元用快速幂求（费马小定理）。不懂费马小定理和快速幂的可以看我之前写过的一篇文章

代码

def fast_pow(a, b):
    res = 1
    while b:
        if b & 1:
            res = res * a % mod
        a = a * a % mod
        b >>= 1
    return res


n = int(input())
ans = 0
mod = 998244353
for i in range(n):
    x, y = map(int, input().split())
    ans = (ans + 1) * y % mod * fast_pow(y - x, mod - 2) % mod
print(ans)

灭鼠先锋

题目描述

灭鼠先锋是一个老少咸宜的棋盘小游戏，由两人参与，轮流操作。

灭鼠先锋的棋盘有各种规格，本题中游戏在两行四列的棋盘上进行。游戏的规则为：两人轮流操作，每次可选择在棋盘的一个空位上放置一个棋子，或在同一行的连续两个空位上各放置一个棋子，放下棋子后使棋盘放满的一方输掉游戏。

小蓝和小乔一起玩游戏，小蓝先手，小乔后手。小蓝可以放置棋子的方法很多，通过旋转和翻转可以对应如下四种情况：

XOOO XXOO OXOO OXXO
OOOO OOOO OOOO OOOO

其中 O 表示棋盘上的一个方格为空，X 表示该方格已经放置了棋子。
请问，对于以上四种情况，如果小蓝和小乔都是按照对自己最优的策略来玩游戏，小蓝是否能获胜。如果获胜，请用 V 表示，否则用 L 表示。请将四种情况的胜负结果按顺序连接在一起提交。

思路

1.首先看第二个棋盘，小乔下在第一行的第三四个，小蓝必输

2.其次看第四个棋盘，首先排除小乔第一步下在第一行，否则小蓝下次将下在第一行，第二行小乔先下必输。
所以小乔第一步只能下在第二行，只有下面四种状态： （需要自己去枚举一下状态）
第一种：下在第二行的第一个或第四个，枚举一下剩下的情况，是小蓝赢
第二种：下在第二行的第二个或第三个。。。。。。是小蓝赢
第三种：下在第一二个或第三四个。。。。是小蓝赢
第四个：下在第二三个。。。是小蓝赢
3.然后看第三个棋盘，我们已知，第四个是小蓝赢的情况，那小乔下一个棋（第一行第三列）和第四个棋盘一样，那么就是小乔赢，小乔输。
4.最后来看第一个棋盘，小乔下在第一行第三个，有下面几种情况：
第一种：小蓝下一个，则小乔下两个，此后小蓝必输
第二种：小蓝下两个，则小乔下第二行的其中一个，则此后小蓝必输。

print("LLLV")

卡片

问题描述

小蓝有 k 种卡片, 一个班有 n 位同学, 小蓝给每位同学发了两张卡片, 一 位同学的两张卡片可能是同一种, 也可能是不同种, 两张卡片没有顺序。没有 两位同学的卡片都是一样的。

给定 n, 请问小蓝的卡片至少有多少种?

思路

前缀和：不能暴力只能推公式
11 1
12 2
22 2
13 3
23 3
33 3
14 4
24 4
34 4
44 4
k * (k + 1) // 2 >= n
k^2 + k >= n
(k + 1/2) ^ 2 >= 2n + 1/4
k >= (2n + 1/4)^ 0.5 - 1 / 2

代码

n = int(input())
print(math.ceil((2 * n + 1/4) ** 0.5 - 1 / 2))

求阶乘【二分+思维】

问题描述

满足 N ! 的末尾恰好有 K 个 0 的最小的 N 是多少?
如果这样的 N 不存在输出 −1。

思路

求最小的N，不能去枚举N！，虽然python中的int能装很大，但效率不高，首先观察求N！末尾0的个数，其实就看有多少个5的倍数，先出现2的倍数再出现5的倍数，因此肯定能凑成1个0，例如5！=1 * 2 * 3 * 4 * 5就能凑成一个0，同时注意，25！的阶乘是有6个0的，而不是5个0，应为25可以分解成5x5，前面也肯定能分解 出来两个2x2，所以就会突增。同时这是一个递增序列，满足单调性，可以利用二分来解决。

代码

import os
import sys

# 请在此输入您的代码
def cal(n):
  cnt = 0
  while n // 5:
    cnt += n // 5
    n //= 5
  return cnt
k = int(input())
l, r = 0, 10 ** 19
while l + 1 < r:
  m = (l + r) // 2
  if cal(m) >= k:
    r = m
  else:
    l = m
if cal(r) == k: # 判断是否有突增的情况，例如末尾出现5个零的没有，输出-1
  print(r)
else:
  print(-1)

选数异或 【哈希表】

题目描述

给定一个长度为n 的数列A1 ,A2,⋯,An和一个非负整数x, 给定m 次查询,每次询问能否从某个区间[l,r]中选择两个数使得他们的异或等于x 。

思路

如果对每一个区间用x去异或a[i]，再存到map中进行查找，这样会爆时间复杂度。因此，我们可以存A[i]的最右边(i>j)满足A[i] ^ A[j] = x。然后查询A[r]时，只需判断是否≥l即可。我们可以用map来存a^x的下标。然后每次去更新Rightest数组（存的满足A[i] ^ A[j] = x(i > j)是最右边的下标）。

注：当数据量大时，不能在循环里一边判断一边输出，因为每次打印都会进行一次IO操作，这样会消耗大量的时间。而使用列表输出的方式，我们可以将所有的结果存储在一个列表中，然后一次性输出。这样就只需要进行一次IO操作，因此在大量数据时更高效。另外，列表可以很容易地进行排序、筛选、反转等操作，而循环打印则需要重新编写循环打印代码。

代码

import os
import sys

# 请在此输入您的代码
n, m, x = map(int, input().split())
rightest = [0] * (n + 1)  # 创建一个数组，存a[i]与i前面的最近的数a[j]，使得a[j] ^ a[i] = x
pos_left = {}  # 存a的索引
arr = list(map(int, input().split()))
for i, a in enumerate(arr, start=1):
  rightest[i] = max(rightest[i - 1], pos_left.get(a^x, 0))
  pos_left[a] = i

ans = []
for _ in range(m):
  l, r = map(int, input().split())
  if rightest[r] >= l:
    ans.append("yes")
  else:
    ans.append("no")
for val in ans:
  print(val)