python详解(8)——进阶(2):初步算法
目录
一、前言
二、时间复杂度
三、递推
1.简介
2.爬楼梯
3、猴子吃桃
四、递归
1、简介
2、递归求斐波那契数列
3、递归求阶乘
五、穷举法
1、简介
2、百钱买百鸡
编辑
3、组合数字
六、贪心算法
1、简介
2、背包与宝物(中等)
3、跳跃游戏(困难)
七、分治法
1、简介
2、a^b
八、动态规划法
1、简介
九、区分
十、尾声
一、前言
好消息:放假了yeeeeeeeeeeeeee~
更好消息:喜羊羊与灰太狼新剧开播了yeeeeeeeee~
坏消息:要写文
在上一篇文章当中,我们了解了8个排序算法。这只是算法的冰山一角。我们接着来了解和学习。
这次,我们了解的是算法的深入认识及各种方法,还有各种例题。
写作不易,给个三连支持一波!
二、时间复杂度
上一篇文章已经学过了算法的基本定义,这里不再重复阐述。
首先,我们来了解算法的时间复杂度。
时间复杂度,是来衡量一个算法用时的东西。用O符号来记录。
注意,这里面的时间不是真正运行的时间,只是相对于输入的。
时间复杂度常见的有5种:
常数时间O(1)。意思就是无论输入多么复杂,或者多么简单,他所运行的时间都是固定的数值。例如有一个算法是要求一个列表的第一位,代码如下:
def abc(li):
return li[0]这里面,无论输入多么复杂,最终程序的用时都是固定的。
线性时间O(n)。n的意思就是输入规模大小。他的意思就是,所用的时间是和输入规模大小成正比的。这多用于for循环遍历。例如,要把一个列表的每位元素分开输出,代码就是:
def abc(li):
for i in li:
print(i)这里面,列表li越长,运行时间就按正比例关系增加。
对数时间O(log n)。对数时间一般是二分查找的时候。例如大家小时候玩过一个猜数字的游戏:从1-100里的任意一个随机数中,找到一个数字,每次猜测会提示你猜大了还是猜小了。
这个问题的最优解法是:一直在固定的范围内折半猜。例如1-100就猜50,50到100就猜75,这种方法是最快的。
如果要写一个程序来猜这个数,它所用的时间就是log n。这里面的底数是2。
线性对数时间复杂度O(n log n)。是不是有点难理解?
我们之前写的归并排序、快速排序的时间复杂度就是O(n log n)。回味一下快速排序代码:
这里面,我们用一个while循环O(n)一直进行三分O(log n),最后返回。这段程序一直循环进行O(log n),组合在一起就是O(n log n)。
平方时间O(n^2)。平方时间运行是有点慢的。典型的示例就是嵌套循环。例如,把一个数组的每两个元素进行比较,看能组合多少个。这么简单的代码直接return len(li)**2就行了,可有一个大聪明非得整一个嵌套循环,代码就是:
def abc(li):
count=0
for i in li:
for j in li:
count+=1
return count这里面,它的时间复杂度就是就是O(n^2)。这属于一种低效的时间复杂度。
指数时间O(2^n)。他运行的时间呈指数型增长。
程序实例:一个递归版本的斐波那契数列。
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)这里面,运行时间就是指数增长的。
除了这五种常用的时间复杂度,还有几种。
O(n^3),立方时间,一般是三重嵌套循环。
O(m*n),m*n时间,m和n分别代表两个输入的大小。一个量不变,运行时间就会随着另一个量的增长而增长。如果两个量都变,运行时间则会更慢。
O(log log n),双对数时间,一般是一些基于分治法、反证法的算法。
O(sqrt(n)),根号时间,一般是求解质数、因子的问题。
O(n!),阶乘时间,一般是用来组合的暴力解法。例如我们都熟悉的问题:n把锁n个钥匙,至少要试几次才能打开所有锁。一直尝试来解的话,他的时间复杂度就是O(n!)。
除此之外还有好多种。这里不再解释。
另外,时间复杂度是有最优和最差的。例如一个不稳定的排序算法,他的运行时间也不固定。
在上一篇文章中:
冒泡排序:O(n^2)
快速排序:最优O(n log n),最差O(n^2)
插入排序:最优O(n),最差O(n^2)
选择排序:O(n^2)
计数排序:O(n+k)。这是一种特殊的时间,n是列表长度,k是列表里最大的数。
归并排序:O(n log n)
基数排序:O(d(n+k))。还是一种特殊的时间。其中n是列表长度,k是最大元素的范围,d是最大元素的位数。
bogo排序:啥也不是
三、递推
1.简介
接下来,我们学习算法中的递推法。
递推,就是一步一步由已知推向未知。最后得出需要的结果。
例如,推算出斐波那契数列中,某一个值后面的那一个数,只给你1,1为起始条件,这就要用到递推的方法。先推算第三位,再第四位,再第五位······直到推算出结果。代码如下:
def Fibonacci(num):
a = 1
b = 1
while True:
a = a+b
if a >= num:
return a
b = a+b
if b >= num:
return b
num = int(input())
print(Fibonacci(num))输入:114
输出:144
就像这样,逐步推出结果。
有些递推法解决的问题,表面很复杂,但一般有这两种方法提供思路:
1.列举法,列举一些结果,看他们有什么规律。
2.关系式法,列出来每个量之间的关系式,可以是数列。
递推分为顺推和倒推,倒推就是根据一个问题的结果来输出他的条件。
话不多说,我们直接来几道例题。
2.爬楼梯
来一道经典的爬楼梯问题。
一个楼梯有n阶台阶,你每次可以选择一次跨2格或者一次跨1格,问你爬上去有多少个解法?
这题,你们可能只是不会写代码,我连数学解法都不会······我们来找一下规律:
1:1个
2:2个
3:3个
4:5个
5:8个
6:13个
······1,2,3,5,8,13,熟悉吗?
这是斐波那契数列。按照斐波那契数列的方法来推就行了。
def palouti(num):
if num == 1 or not num:
return num
a = 1
b = 1
c = 1
while True:
a = a+b
c += 1
if c == num:
return a
b = b+a
c += 1
if c == num:
return b
while True:
num=int(input())
print(palouti(num))最终代码。
3、猴子吃桃
猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第二天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想吃时,只剩下一个桃子了。求第一天共摘多少个桃子。
我们先不管这个猴子是不是有什么大饼,也不管他的饮食规不规律,先列关系式再说。
我们用关系式来解决。
第n天的桃子数量=第n-1天的桃子数量/2-1
则,第n-1天的桃子数量=(第n天的桃子数量+1)*2
第十天有1个桃子,我们只要把他+1,再*2就行,循环10次。
代码:
def abc():
num = 10
a = 1
while True:
a = (a+1)*2
num -= 1
if num == 1:
return a
print(abc())四、递归
1、简介
递归上一篇文章已经讲过了,我们再回味一下。
递归,就是通过一个函数在程序内调用自身来减少代码量。递归的方法需要一个边界条件,不然会无限循环;当到达递归边界时,程序会一层层向上返回,最后得出想要的结果。
可以理解成一个傻*查字典,他查了一个词,发现这个词语解释里面有不会的词,于是又去查第二个词,但是第二个词的解释里面还有不会的词,于是就去查第三个······直到有一个词语的注释他可以看懂(递归边界条件),这时候,他就可以理解倒数第一个词,倒数第二个词······最后理解最开始的词。
递归有3个特点:
1、必须有一个明确的结束条件,就是递归边界。
2、每次进入更深一层的递归,计算量相比于上一层都会有所减少。
3、递归次数过多会导致栈溢出。
递归注重的是简洁与优雅,至于速度那玩意儿谁爱考虑谁考虑。
递归中,你创建的每一轮递归都叫做栈。栈的数量是有限制的。一般是在1000左右。超过就会报错。这叫做栈溢出。
话不多说,直接上题:
2、递归求斐波那契数列
求斐波那契数列的第n个数。
这题大家可能感觉无从下手,因为递归写起来比较难,但是我们只要理清一个关系:
S(n)=S(n-1)+S(n-2)
S为斐波那契数列,n表示第n项。
然后我们可以一直求下去。
S(n-1)=S(n-2)+S(n-3)
S(n-2)=S(n-3)+S(n-4)
······
最后一直到斐波那契数列的第1、2位,这就是递归边界条件。直接返回1。因为斐波那契数列的第1和2项都是1。
代码:
def Fib(n):
if n == 1 or n == 2:
return 1
return Fib(n-1) + Fib(n-2)
n=int(input())
print(abc())行量这么少也是十分的神奇,但是时间复杂度达到了恐怖的O(2^n)。
3、递归求阶乘
接下来,我们用递归求n的阶乘。
我们找一下规律。
1!=1
2!=2x1!=2
3!=3x2!=6
4!=4x3!=24
5!=5x4!=120就是这样。思路已经十分明确了,相信大家自己也能写出来代码。注意:当n=0或者1时为递归边界条件,直接返回1。代码:
def f(x):
if x == 0:
return 1
elif x == 1:
return 1
else:
return(x * f(x-1))
while True:
print(f(int(input())))五、穷举法
1、简介
穷举,顾名思义就是把问题结果所有可能出现的解试一遍,直到试出答案。
这种方法出现率很少,一是因为大多数算法用不着穷举,二是因为时间复杂度高。
大家应该能想到,穷举方法的时间肯定是很慢的。提升时间的方法就是:不用穷举尽量缩小穷举范围。前提是你能确保答案在这个范围内。
不多说了,先来几道例题:
2、百钱买百鸡
一个人有100块钱,雄鸡5块1只,母鸡3块1只,小鸡1块3只,他100块钱刚好买了100只,问雄鸡母鸡小鸡各买了几只(列出所有可能,不会有一类鸡买了0只)。
假设雄鸡x只,母鸡y只,小鸡z只:
x+y+z=100
5x+3y+z/3=100
(x,y,z∈N+)穷举法解决这个问题,首先要明确每类鸡最多能买几只。
雄鸡最多20只,因为21只就超过了100块钱。母鸡最多33只。小鸡最多300只,但是他买了100只鸡,所以最多100只。
接下来,就是穷举遍历了。如果满足上述2式则print。
我们还有一个加速点:小鸡。因为小鸡1块3只,所以小鸡的数量一定是3的倍数,所以我们遍历小鸡的时候,步长可以设置为3。
最终代码:
for x in range(1, 21):
for y in range(1, 34):
for z in range(3, 100, 3):
if (x*5 + y*3 + z/3 == 100 and x+y+z == 100):
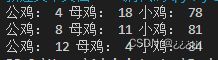
print("公鸡:",x,"母鸡:",y,"小鸡:",z)有人有疑问了:遍历雄鸡是1到20,母鸡是1到33,都很正常,遍历小鸡的时候为什么遍历的是3到99呢?
步长是3,不代表是要遍历3的倍数。如果是正常遍历1到100,则遍历的是1,4,7,10······如果遍历的是3-100,则遍历的是3,6,9······这才是正确的,而且不会出现多出或遗漏。最终结果:
3、组合数字
有三个数为a,b,c,他们的和为19,取值范围为1-9,问有多少种可能?(a!=b!=c)
很简单,先创建一个计数变量。每一个数都遍历1到9,如果a+b+c=19,且三者都不相等则将计数变量自增。最后输出计数变量。最终结果为30。
count = 0
for a in range(1, 10):
for b in range(1, 10):
for c in range(1, 10):
if a+b+c == 19 and a != b and a != c and b != c:
count += 1
print(count)六、贪心算法
1、简介
这种算法使用率很高,通常是一步一步进行,总是会做出从当前来看最优的选择。他不能求出所有问题的最优解,但能求出大部分问题的近似最优解。
因为大多数问题不会让你求近似最优解,你如果要在这类问题上使用贪心算法,就必须先证明:结果一定最优。
不说了,看例题!
2、背包与宝物(中等)
有一个人背着背包,他最多能背动150单位重的东西。现在有以下宝物:
| A | B | C | D | E | F | G | |
| 重量 | 35 | 30 | 60 | 50 | 40 | 10 | 25 |
| 价格 | 10 | 40 | 30 | 50 | 36 | 40 | 30 |
问:背哪些宝物可以价值和更高?
这个问题,用贪心算法就只需要求出重量与价格比值,之后从大到小排列。
我们来注意一下,如果遍历到最后怎么办?比如遍历到最后还有35单位,宝物还有BFG没装,那么该选择哪个?
贪心算法会先选择F,之后选择B。但是程序会发现超重了,这时候,贪心算法的弱点就暴露出来了:有的问题求不出来最优解。程序会放弃选择,直接留下25单位的空间浪费。
如果在超重时进行侦测并且找到不超重且最贵的宝物进行获取,那我们可以想象,如果宝物是这样的,背包容积114518:
A宝物重114514,钱1919810
B宝物重3,钱8
C宝物重0.5,钱1
如果让上述的算法进行筛选,他就会选择A,再选择D。然后就没有然后了。
只能再加强一下算法,进行多个物品的选择,那这样就又回到了上述程序。
显然:如果求出来最优解,需要递归。
我们给原问题增加一个条件:宝物可以分割,并且重量与价值比不变,不然寿命要没了。这样遇到超重直接给他分割就行。
代码懒得写辣!
3、跳跃游戏(困难)
给定一个非负整数数组,最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断是否能够跳完列表。
用贪心算法解决,我们要解决的就是:当自己在一个位置上时,尽力跳得远。
侦测流程:
1、设自己所在位置为n,n的后n位的列表为li,其中第一个数字为k。如果n-k 2、反之,如果n-k>=n到k的距离,跳过去就不会赚,不能跳。 3、如果2成立,我们则让k侦测第二个数,还是不能再侦测第3个数······只要有成立就跳到那个数字上,不成立则继续下一个数字的判断。如果li里面的数字都亏了,则不能逃出这里,输出False。 4、如果更新n、li的时候出现异常则是遍历到了末尾导致越界,直接输出True。 步骤很复杂?简化一下: 具体代码就不写了。作者没有去写出来并运行代码,如果有不河里的地方请指出! 分治法,就是把一个问题分成若干个小问题最后连起来。和贪心算法是不是有点相似?最大的区别就是:贪心算法是走到哪一步考虑哪一步,分治法是直接把大问题分成若干个小问题再分别解决。 还是很好理解,直接看题: 求a^b。这里不是简单地a^b, 你们可能感觉:这么简单的一个幂运算怎么能分呢? 我们来分治一下: 我们要做的,就是把负奇、负偶、正奇、正偶这四种情况考虑。是不是有点像数学的分类讨论? 如果a是偶数的话,也就是a%2==0: 如果a是奇数的话,也就是a%2==1: 如果b是负数,还是上面那一套方法,再用1去除就行。 完成这个代码呢,要浅浅得用一下递归。准确来说不算递归,就是调用一两次自己而已。代码: 动态规划,就是把一个大的复杂问题分成若干小问题,求出这些小问题的最优解再合起来。这些小问题都具有相同特征。 动态规划的主旨就是动态和规划。 是不是又像贪心又像分治? 他仨长得确实有点像,后面会进行详细讲解。不多说了,来几道例题: ······ 我去,救命,一道简单的例题都搜不出来。跳过跳过。 这么多算法方法之间,大家可能察觉出了很多联系。接下来,我们将比较相似的方法进行区分: 递推与递归的区别: 递推是数学上的概念,指的是递推式、数列等等这些,将思想迁移进行应用。 递归则是一个函数调用自身,来减小代码量。 分治法和动态规划法的区别: 二者都要将问题分成几个小问题再合并求解。 不同的是在分治法中,小问题之间没有太大联系。 而在动态规划法中,则是多个同样的小问题的重叠,避免对同一个问题的重复计算。 分治法和贪心算法的区别: 分治法是将问题分成多个独立小问题再分别求解。 贪心算法则是将问题分成了多个阶段,每个阶段做出局部最优选择。 分治法需要合并最后的独立小问题,贪心算法则是走哪儿算哪儿,不需要合并。 我真的不是故意花一个月屑文的······ 写作不易,求个三连支持~ -----------------------------------------------------end----------------------------------------------------------设置n、li
死循环:
用k遍历range(li):
比较 n-li(k)和k+1,如果<:
错误尝试:
更新n、li并break退出循环
如果报错,就是说已经遍历到了末尾导致越界
返回True
如果循环是正常退出:
返回False七、分治法
1、简介
2、a^b
是王维诗里的a^b啊不,是用分治法求a^b。如果a是负数{
如果a是奇数
如果a是偶数
}
如果a是正数{
如果a是奇数
如果a是偶数
}![]() =
= ![]() =
= ![]()
![]() =
= ![]() =
= ![]()
def _pow(a, b):
if a == 0 and b == 0:
return None
elif b == 0:
return 1
elif a == 0:
return 0
elif b < 0:
return 1/_pow(a, -b)
elif b%2 == 0:
return _pow(a*a, b//2)#利用积的乘方:a^n*b^n=(ab)^n,这里a=b
else:#仅剩的选择:b为正奇数
return _pow(a*a, b//2)*a
while True:
a=int(input())
b=int(input())
print(_pow(a, b))八、动态规划法
1、简介
九、区分
十、尾声