LeetCode 热题100道（中等题整理）

1. 两数相加

示例：

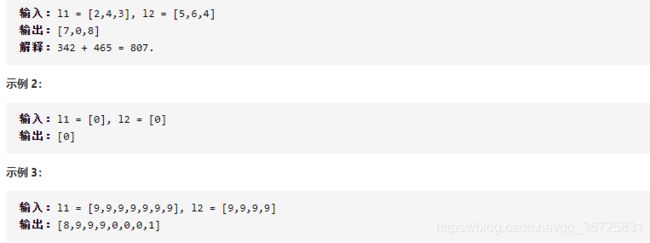
分析：
老实人本来准备把两个链表转成整型相加再转回链表，被[1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]教做人了，unsigned long都顶不住…

注意链表是实际数字的逆序，所以可以直接遍历相加，注意进位就行。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        int carry = 0;
        ListNode *sumList = new ListNode(-1);
        ListNode *sumNode = sumList;
        while (l1 != nullptr || l2 != nullptr){
            int x = l1 != nullptr ? l1->val : 0;
            int y = l2 != nullptr ? l2->val : 0;
            int sum = x + y + carry;
            if(sum >= 10){
                carry = 1;
                sum = sum - 10;
            }else{
                carry = 0;
            }
            sumNode->next = new ListNode(sum);
            l1 = l1 != nullptr ? l1->next : nullptr;
            l2 = l2 != nullptr ? l2->next : nullptr;
            sumNode = sumNode->next;
        }
        if(carry != 0){
            sumNode->next = new ListNode(carry);
        }
        return sumList->next;
    }
};

执行用时：24 ms, 在所有 C++ 提交中击败了93.87%的用户
内存消耗：69.4 MB, 在所有 C++ 提交中击败了62.48%的用户

2. 无重复字符的最长子串

示例：

分析：
滑动窗口，判断重复字符，可以用unorderd_set,也可以遍历查找。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int start = 0, end = 0;
        int len = s.size();
        int max_count = 0, temp_count = 0;
        char temp_char;
        while(end < len){
            temp_char = s[end];
            for(int i = start; i < end; i++){
                //出现重复字符，开始位置移到重复的下一位
                if(temp_char == s[i]){
                    start = i + 1;
                    break;
                }
            }
            end++;
            temp_count = end -start;
            max_count = max(max_count , temp_count);
        }
        return max_count;
    }
};

执行用时：4 ms, 在所有 C++ 提交中击败了97.69%的用户
内存消耗：6.7 MB, 在所有 C++ 提交中击败了91.11%的用户

用哈希，std::unordered_set

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        // 哈希集合，记录每个字符是否出现过
        unordered_set<char> occ;
        int n = s.size();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        // 枚举左指针的位置，初始值隐性地表示为 -1
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.erase(s[i - 1]);
            }
            while (rk + 1 < n && !occ.count(s[rk + 1])) {
                // 不断地移动右指针
                occ.insert(s[rk + 1]);
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = max(ans, rk - i + 1);
        }
        return ans;
    }
};

3. 最长回文子串

分析：

回文的意思是正着念和倒着念一样，如：上海自来水来自海上

法一：翻转字符串求公共串，结果超时了…

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.length()==1) return s;//大小为1的字符串必为回文串
        string rev=s;//rev存放s反转结果
        string res;//存放结果
        std::reverse(rev.begin(),rev.end());
        if(rev==s) return s;
        int len=0;//存放回文子串的长度
        for(int i=0;i<s.length();i++)//查找s与rev的最长公共子串
        {
            string temp;//存放待验证子串
            for(int j=i;j<s.length();j++)
            {
                temp=temp+s[j];
                if(len>=temp.length())
                    continue;
                else if(rev.find(temp)!=-1)//在rev中找到temp
                {
                    string q=temp;//q用来验证temp是否是回文子串
                    std::reverse(q.begin(),q.end());
                    if(q==temp)
                    {
                        len=temp.length();
                        res=temp;
                    }
                }
                else break;
            }
            temp="";
        }
        return res;
    }
};

法二 ： 中心扩展法，（传参用引用效率高）

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        if(len==0||len==1)
            return s;
        int start=0;//记录回文子串起始位置
        int end=0;//记录回文子串终止位置
        int mlen=0;//记录最大回文子串的长度
        for(int i=0;i<len;i++)
        {
            int len1=expendaroundcenter(s,i,i);//一个元素为中心
            int len2=expendaroundcenter(s,i,i+1);//两个元素为中心
            mlen=max(max(len1,len2),mlen);
            if(mlen>end-start+1)
            {
                start=i-(mlen-1)/2;
                end=i+mlen/2;
            }
        }
        return s.substr(start,mlen);
        //该函数的意思是获取从start开始长度为mlen长度的字符串
    }
private:
    int expendaroundcenter(string &s,int left,int right)
    //计算以left和right为中心的回文串长度
    {
        int L=left;
        int R=right;
        while(L>=0 && R<s.length() && s[R]==s[L])
        {
            L--;
            R++;
        }
        return R-L-1;
    }
};

法三 ： 动态规划

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        if(len==0||len==1)
            return s;
        int start=0;//回文串起始位置
        int max=1;//回文串最大长度
        vector<vector<int>>  dp(len,vector<int>(len));//定义二维动态数组
        for(int i=0;i<len;i++)//初始化状态
        {
            dp[i][i]=1;
            if(i<len-1&&s[i]==s[i+1])
            {
                dp[i][i+1]=1;
                max=2;
                start=i;
            }
        }
        for(int l=3;l<=len;l++)//l表示检索的子串长度，等于3表示先检索长度为3的子串
        {
            for(int i=0;i+l-1<len;i++)
            {
                int j=l+i-1;//终止字符位置
                if(s[i]==s[j]&&dp[i+1][j-1]==1)//状态转移
                {
                    dp[i][j]=1;
                    start=i;
                    max=l;
                }
            }
        }
        return s.substr(start,max);//获取最长回文子串
    }
};

4. 盛最多水的容器

分析：
双指针法：
水量 = 两个指针指向的数字中较小值∗指针之间的距离
理解：双指针代表的是 可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示 数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置，就表示我们认为 这个指针不可能再作为容器的边界了。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right =  height.size() - 1;
        int max_area = 0, temp_area = 0;
        while(left < right){
            temp_area = (right - left) * min(height[left], height[right]);
            max_area = max(max_area, temp_area);
            if(height[left] < height[right]){
                left++;
            }else{
                right--;
            }
        }
        return max_area;
    }
};

5. 三数之和

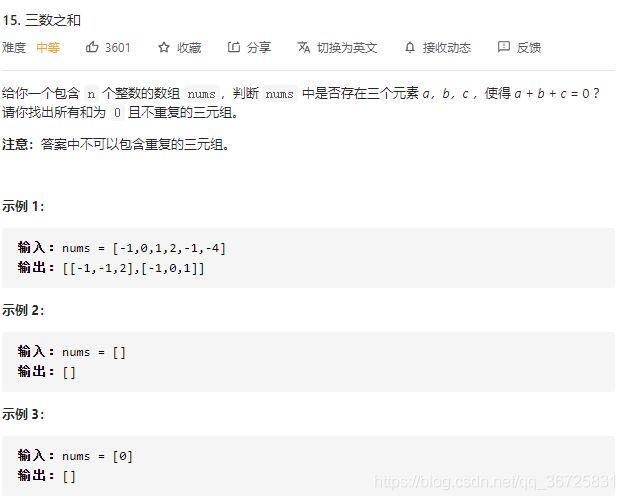
分析：
方法：首先确定一个数，然后利用双指针去找另外的两个数，注意一些去重的判断。

四数之和方法类似，固定两个数。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int len =  nums.size();
        vector<vector<int>> res;
        if(len < 3)
            return res;
        sort(nums.begin(), nums.end());
        
        //固定第一个数为nums[i]
        for(int i = 0; i <len ; i++){
            // 第一个数大于 0，后面都是递增正数，不可能相加为零了
            if(nums[i] > 0){
                return res;
            }
            // 第一个数相同，pass
            if(i > 0 && nums[i] == nums[i-1]){
                continue;
            } 
            //双指针法
            int left = i + 1, right = len -1;
            while(left < right){
                if(nums[left] + nums[right] + nums[i] > 0){
                    right--;
                }
                else if(nums[left] + nums[right] + nums[i] < 0){
                    left++;
                }
                else{
                    res.push_back(vector<int>{nums[i], nums[left], nums[right]});
                    left++;
                    right--;
                    
                    //第一个数固定后，第二个数和第三个数去重
                    while(left < right && nums[left] == nums[left-1]){
                        left++;
                    }
                    while(left < right && nums[right] == nums[right+1]){
                        right--;
                    }
                }
            }
        }
        return res;
    }
};