考研数据结构上机题【36个模块77道题】5万字帮助你学会考研算法【完结篇】
专注 效率 记忆
预习 笔记 复习 做题
欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录)
文章字体风格:
红色文字表示:重难点★✔
蓝色文字表示:思路以及想法★✔
如果大家觉得有帮助的话,感谢大家帮忙
点赞!收藏!转发!
本博客带大家一起学习,我们不图快,只求稳扎稳打。
由于我高三是在家自学的,经验教训告诉我,学习一定要长期积累,并且复习,所以我推出此系列。
只求每天坚持40分钟,一周学5天,复习2天
也就是一周学10道题
60天后我们就可以学完81道题,相信60天后,我们一定可以有扎实的代码基础!我们每天就40分钟,和我一起坚持下去吧!
qq群:878080619
【考研408-数据结构(笔试)】
- 一、排序
-
- 1. 成绩排序(清华大学考研机试题)
-
-
- 考点:结构体排序
-
- 在结构体中定义排序
- 使用比较器定义排序
- 注意问题:需要处理 值相等时 先后顺序
-
- 2. 成绩排序2( 清华大学考研机试题 )
- 二、进位制
-
- 1. 进制转换(清华大学考研机试题)
-
-
- 本题考点
-
- 1. 大数除法
- 2. 十进制转二进制 步骤
-
- 2. 进制转换2(清华大学考研机试题)
-
-
- 考点:M进制转N进制
-
- 和10进制转2进制 不一样的就是:短除时的 进位一个是10,而另一个是a仅此而已
-
- 三、链表
-
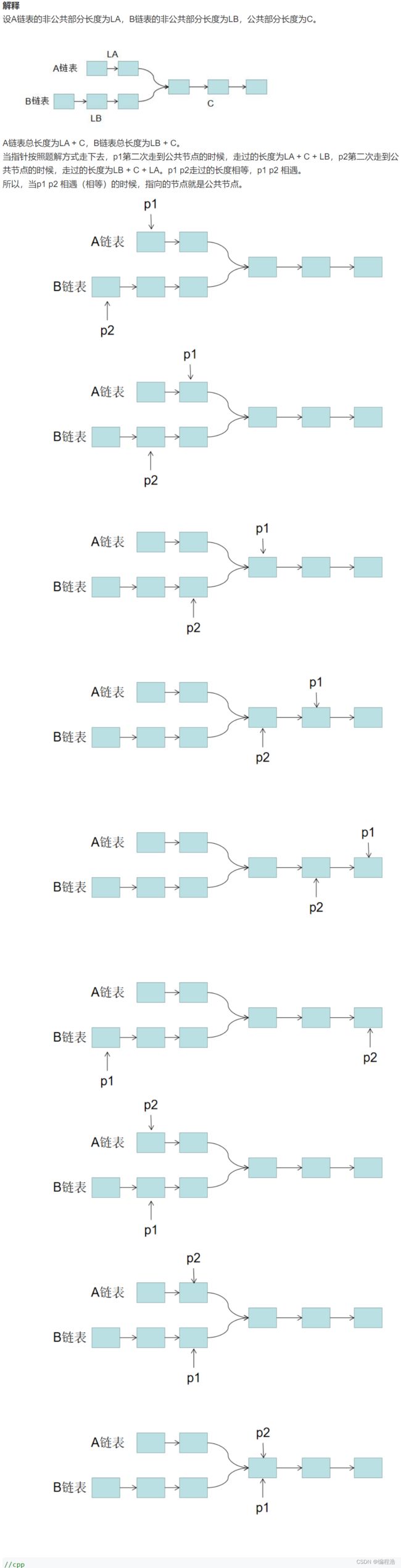
- 1. 两个链表的第一个公共结点
- 2. 筛选链表( 2015年全国硕士研究生招生考试 )
-
-
- 考点:删除节点
-
- 需要两个指针,一个前一个后删除(所以比较的时候,比较p->next->val比较好)
-
- 3. 重排链表( 2019年全国硕士研究生招生考试 )
-
-
- 考点:1. 链表反转;2. 链表合并
-
- 四、日期问题
-
- 1. 日期累加( 北京理工大学考研机试题 )
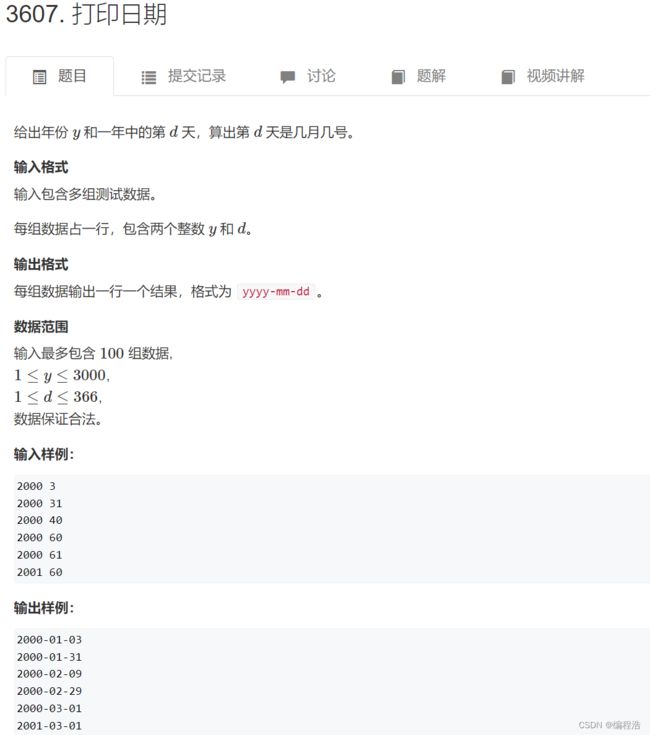
- 2. 打印日期( 华中科技大学考研机试题 )
- 五、表达式求值
-
- 1. 表达式求值
- 六、树的遍历( 递归 )
-
- 1. 二叉树的带权路径长度
- 2. 重建二叉树
-
-
- 构建二叉树的两种情况
-
- 七、二叉搜索树与表达式树
-
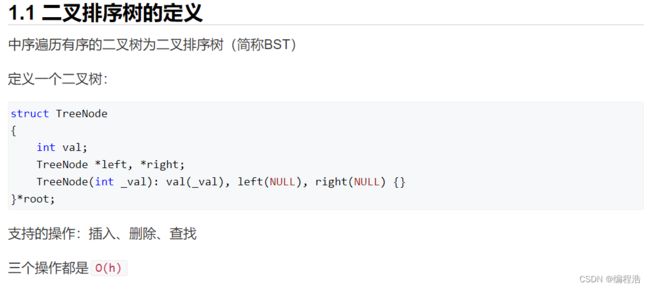
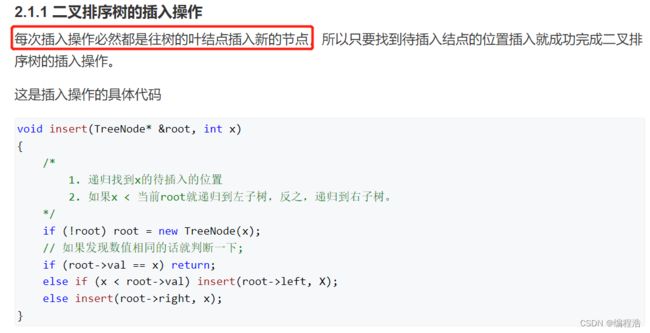
- 1. 二叉排序树(中序遍历是有序的)
- 2. 表达式树
- 八、Huffman树
-
- 1. 合并果子
- 2. 荷马史诗
-
-
- 考点:( 构建深度最小的哈夫曼树 )利用pair
- 考点:( k进制哈夫曼树需要补零节点 )
-
- 八、拓扑排序
-
- 1. 有向图的拓扑序列
- 九、最小生成树、最短路
-
- 1. Prim算法求最小生成树(和dijk算法差不多)
- 2. Dijkstra求最短路 I
- 3. Floyd求最短路
- 4. spfa求最短路
- 十、哈希表
-
- 1. 模拟散列表
-
-
- 开散列方法(拉链法)
- 开放寻址法代码
-
-
- 本质:(最多存1e5个数)
-
-
- 2. 未出现过的最小正整数( 2018年全国硕士研究生招生考试 )
- 十一、KMP
- 十二、排序
-
- 1. 快速排序
- 2. 整数集合划分
- 十三、多路归并
-
- 1. 三元组的最小距离(2020年全国硕士研究生招生考试)
- 十四、摩尔投票法
-
- 1. 数组中出现次数超过一半的数字
- 十五、DFS
-
- 1. 全排列( 北京大学考研机试题 )
- 2. 八皇后( 北京大学考研机试题 )
- 十六、模拟
-
- 1. 反序输出( 清华大学考研机试题 )
-
-
- 考点:reverse(s.begin(), s.end());
-
- 2. 特殊乘法( 清华大学考研机试题 )
- 3. 众数( 清华大学考研机试题 )
- 4. 糖果分享游戏
- 十七、递推
-
- 1. 递推数列( 清华大学考研机试题 )
- 2. 吃糖果( 北京大学考研机试题 )
- 十八、BFS
-
- 1. 玛雅人的密码
- 2. 等差数列
- 十九、字符串处理
-
- 1. 首字母大写
- 2. 日志排序
- 3. 字符串转换整数
- 二十、递归,画图
-
- 1. 重复者
- 二十一、背包问题
-
- 1. 01背包
- 2. 神奇的口袋( 体积恰好是 )
- 3. 整数拆分
- 二十二、高精度
-
- 1. N的阶乘
-
- 做法:预处理
- 2. 基本算术
- 3. 整数查询
- 二十三、因式分解
-
- 1. 质因数的个数
- 2. 约数个数
- 3. 阶乘的末尾0(上海交通大学考研机试题)
- 4. 整除问题(上海交通大学考研机试题)
- 二十四、枚举
-
- 1. 与7无关的数 (北京大学考研机试题)
- 2. 打印极值点下标( 北京大学考研机试题 )
- 3. 最简真分数( 北京大学考研机试题 ) 【真分数】
- 4. 买房子 ( 北京大学考研机试题 )【算立方和平方】
- 5. Special数(北京邮电大学考研机试题)
- 二十六、位运算
-
- 1. 位操作练习(北京大学考研机试题)
- 2. 二进制数(北京邮电大学考研机试题)
- 二十七、矩阵
-
- 1. 旋转矩阵(北京航空航天大学考研机试题)
- 2. 矩阵幂【矩阵相乘】(北京邮电大学考研机试题)
-
-
- 两个矩阵相乘结果
-
- 3. C翻转(北京邮电大学考研机试题)
- 二十八、计算几何
-
- 1. 球的计算
- 2. 点的距离
-
-
- 重新定义类的相减
-
- 3. 直角三角形
- 二十九、前缀和
-
- 1. 最长平衡串(北京邮电大学考研机试题)
- 三十、推公式
-
- 1. 数字台阶
- 2. 整数和
- 3. 弹地小球
- 三十一、最短路
-
- 1. 我想回家(北京大学考研机试题)
- 2. 最短路径
- 3. 最短路径
- 三十二、思维题
-
- 1. 棋盘遍历问题(上海交通大学考研机试题)
- 三十三、哈希表
-
- 1. 子串计算(北京大学考研机试题)
-
-
- map自动排序
-
- 2. 查找(北京邮电大学考研机试题)
-
-
- unordered_set(通过count(x)==0判断是否存在)
-
- 3. 单词识别(北京理工大学考研机试题)
- 三十四、双指针
-
- 1. 最小面积子矩阵
-
-
- 算法1:二维前缀和
- 算法2:一维前缀和 + 双指针
-
- 三十五、序列型DP
-
- 1. 最大序列和(清华大学考研机试题)
- 2. 最长ZigZag子序列
- 三十六、红黑树和并查集
-
- 1. 合并集合
一、排序
1. 成绩排序(清华大学考研机试题)
考点:结构体排序
在结构体中定义排序
#include 使用比较器定义排序
#include注意问题:需要处理 值相等时 先后顺序
在结构体中定义一个id,记录出现的顺序
// package Test;
import java.lang.reflect.Array;
import java.util.Arrays;
import java.util.Scanner;
/**
* @Author zh
* @Date 2023/8/8 19:10
* @PackageName:Test
* @ClassName: Main
* @Description: TODO
* @Version 1.0
*/
class Student{
int grade;
String name;
public Student(int grade,String name){
this.grade = grade;
this.name = name;
}
}
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int a = scanner.nextInt();
Student[] students = new Student[N];
for(int i = 0; i < N; i++){
String name = scanner.next();
int grade = scanner.nextInt();
students[i] = new Student(grade,name);
}
if(a == 1){
Arrays.sort(students,(o1, o2) -> {
return o1.grade-o2.grade;
});
}else{
Arrays.sort(students,(o1, o2) -> {
return o2.grade-o1.grade;
});
}
for(Student x : students){
System.out.println(x.name + " " + x.grade);
}
}
}
2. 成绩排序2( 清华大学考研机试题 )
#include import java.util.Arrays;
import java.util.Scanner;
class Student{
int id;
int grade;
public Student(int id,int grade){
this.id = id;
this.grade = grade;
}
}
class Main{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
Student[] students = new Student[n];
for(int i = 0; i < n; i++){
int id = scanner.nextInt();
int grade = scanner.nextInt();
students[i] = new Student(id,grade);
}
Arrays.sort(students,(o1, o2) -> {
if(o1.grade == o2.grade){
return o1.id-o2.id;
}
return o1.grade-o2.grade;
});
for (Student x : students){
System.out.println(x.id + " " + x.grade);
}
}
}
二、进位制
1. 进制转换(清华大学考研机试题)
本题考点
1. 大数除法
可以csdn搜索一下
关键就是vector的使用 和 除法步骤记得就好
就好比用 代码模拟出 草稿纸上的除法运算
2. 十进制转二进制 步骤
代码看不懂可以,只需明白逻辑,然后自己写即可
一定自己写出来,才明白
#include2. 进制转换2(清华大学考研机试题)
考点:M进制转N进制
和10进制转2进制 不一样的就是:短除时的 进位一个是10,而另一个是a仅此而已
#include 三、链表
1. 两个链表的第一个公共结点
//cpp
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *p1 = headA;
ListNode *p2 = headB;
while (p1 != p2) {
if(p1 != NULL)//p1没有走到结尾
p1 = p1->next;//p1指向下一个节点
else//p1走到结尾
p1 = headB;//p1指向另一个链表头
if(p2 != NULL)//p2没有走到结尾
p2 = p2->next;//p2指向下一个节点
else //p2走到结尾
p2 = headA;//p2指向另一个链表头
}
return p1;
}
};
2. 筛选链表( 2015年全国硕士研究生招生考试 )
考点:删除节点
需要两个指针,一个前一个后删除(所以比较的时候,比较p->next->val比较好)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* filterList(ListNode* head) {
bool st[10001] = {};
st[abs(head->val)] = true;
for (auto p = head; p->next;) {
int x = abs(p->next->val);
if (st[x]) {
auto q = p->next;
p->next = q->next;
delete q;
} else {
p = p->next;
st[x] = true;
}
}
return head;
}
};
3. 重排链表( 2019年全国硕士研究生招生考试 )
考点:1. 链表反转;2. 链表合并
class Solution {
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
public:
void rearrangedList(ListNode* head) {
// 若只有一个元素,则不需要操作
if (!head->next) {
return;
}
// 计算链表长度
int len = 0;
for (auto p = head; p; p = p->next) {
len++;
}
// 移动到链表中间处
int mid = (len + 1) / 2;
auto a = head;
for (int i = 0; i < mid - 1; i++) {
// 由于该链表没有设头结点,head 就是具有值的结点,因此到 mid - 1
a = a->next;
}
// 反转后半段链表,b在前,c在后
auto b = a->next, c = b->next;
// a->next 是为了从中间将链表截断;b->next 是因为此时的 b 是反转后链表的结尾元素
a->next = b->next = NULL;
while (c) {
auto temp = c->next;
c->next = b;
b = c;
c = temp;
}
// 合并链表,注意此时 b 指向反转链表头部,c 指向 NULL
for (auto p = head, q = b; q;) {
auto qq = q->next;
// 插入结点
q->next = p->next;
p->next = q;
// 移动p和q
p = q->next;
q = qq;
}
}
};
四、日期问题
1. 日期累加( 北京理工大学考研机试题 )
#include 2. 打印日期( 华中科技大学考研机试题 )
#include 五、表达式求值
1. 表达式求值
#include 六、树的遍历( 递归 )
1. 二叉树的带权路径长度
class Solution {
public:
int sum(TreeNode* root, int level) {
if(!root) return 0;
if(!root->left && !root->right) {
return root->val * level;
}
return sum(root->left, level + 1) + sum(root->right, level + 1);
}
int pathSum(TreeNode* root) {
return sum(root, 0);
}
};
2. 重建二叉树
构建二叉树的两种情况
构建二叉树的两种情况【根据前序遍历和中序遍历 构造树】【根据后序遍历和中序遍历 构造树】

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
unordered_map<int,int> pos;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
for (int i = 0; i < n; i ++ )
pos[inorder[i]] = i;
return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
}
TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
{
if (pl > pr) return NULL;
int k = pos[pre[pl]] - il;
TreeNode* root = new TreeNode(pre[pl]);
root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
return root;
}
};
七、二叉搜索树与表达式树
1. 二叉排序树(中序遍历是有序的)
首先我们要清楚:
二叉排序树的特点是
中序遍历(左根右)是有序的
所以如果删除的根节点有左右子树
那么我们为了保证有序
就要把 根节点左子树的最右边 赋值给根节点
因为根节点左子树的最右边是比根节点小中最大的点
只有这样才能保证删除根节点后
左子树比新的根节点都小
右子树比新的根节点都大
#include
// 如果不存在直接return
if (!root) return;
if (x < root->val) remove(root->left, x);
else if (x > root->val) remove(root->right, x);
else
{
if (!root->left && !root->right) root = NULL;
else if (!root->left) root = root->right;
else if (!root->right) root = root->left;
else
{
auto p = root->left;
while (p->right) p = p->right;
root->val = p->val;
remove(root->left, p->val);
}
}
}
// 输出数值 x 的前驱(前驱定义为现有所有数中小于 x 的最大的数)。
int get_pre(TreeNode* root, int x)
{
if (!root) return -INF;
if (root->val >= x) return get_pre(root->left, x);
else return max(root->val, get_pre(root->right, x));
}
// 输出数值 x 的后继(后继定义为现有所有数中大于 x 的最小的数)。
int get_suc(TreeNode* root, int x)
{
if (!root) return INF;
if (root->val <= x) return get_suc(root->right, x);
else return min(root->val, get_suc(root->left, x));
}
int main()
{
int n;
cin >> n;
while (n--)
{
int t, x;
cin >> t >> x;
if (t == 1) insert(root, x);
else if (t == 2) remove(root, x);
else if (t == 3) cout << get_pre(root, x) << endl;
else cout << get_suc(root, x) << endl;
}
return 0;
}
2. 表达式树
本题就是中序遍历
只要不是叶子节点
就加左括号然后遍历左边
遍历完右边加右括号
class Solution {
public:
string dfs(TreeNode* root) {
if(!root) return "";
if(!root->left && !root->right) {
return root->val;
}
string ret = "";
ret += '(';
ret += dfs(root->left);
ret += root->val;
ret += dfs(root->right);
ret += ')';
return ret;
}
string expressionTree(TreeNode* root) {
return dfs(root->left) + root->val + dfs(root->right);
}
};
八、Huffman树
1. 合并果子
本题就记住哈夫曼树的最简代码如下:
#include 2. 荷马史诗
考点:( 构建深度最小的哈夫曼树 )利用pair
可以忽略这个段,下面有
图中所说的合并的次数,本质其实是根节点的深度
所以优先队列的元素是pair
一个记录权值 一个记录深度
考点:( k进制哈夫曼树需要补零节点 )
题解图中有解释
原题链接
所以优先队列的元素是pair
一个记录权值 一个记录深度
#include 八、拓扑排序
1. 有向图的拓扑序列
原题链接
![]()
这就是一个模板
算法原理可以csdn搜一下
#include 九、最小生成树、最短路
1. Prim算法求最小生成树(和dijk算法差不多)
原题链接
![]()
从1节点出发,每次走最短路径(距离集合的最短路径用d表示)选出最短路径再加到res上
(prim算法和dijkstra算法差不多,只是d的表示含义不同)
#include 2. Dijkstra求最短路 I
![]()
#include 3. Floyd求最短路
![]()
#include 4. spfa求最短路
权值可能为负
所以需要每条路径都走
而不是像dijkstra算法只走一部分
所以spfa算法用普通队列存储即可
并且每个点可能走多次,所以st需要再次false
![]()
#include 十、哈希表
1. 模拟散列表
![]()
开散列方法(拉链法)
就记住有N个链表头节点
对于原数据可以 (x % N + N) % N;找到合适位置插入到头节点
#include 开放寻址法代码
本质:(最多存1e5个数)
#include 2. 未出现过的最小正整数( 2018年全国硕士研究生招生考试 )
![]()
由于我们需要从1去找 是否出现在数组中
如果1去遍历一遍数组
2遍历一遍数组
太麻烦
如何一步到位?
其实可以用
哈希思想
把数组出现的数都映射存储到数组中
如何都没有出现
那么一定是大于数组的个数+1的那个值
class Solution {
public:
int findMissMin(vector<int>& nums) {
int n = nums.size();
vector<bool> hash(n + 1);
for (int x: nums)
if (x >= 1 && x <= n)
hash[x] = true;
for (int i = 1; i <= n; i ++ )
if (!hash[i])
return i;
return n + 1;
}
};
十一、KMP
![]()
KMP是快速帮助 子串A 去匹配 主串B的算法
我们利用next记录
当B和A不匹配的时候,A应该返回B中的哪个位置
所以next应该记录的是B的快速匹配位置
具体逻辑可以搜CSDN
#include 十二、排序
1. 快速排序
![]()
- 快速排序的核心思想是:
大于x的 放到数组右边
小于x的放在数组左边
等于x的放在数组中间 - 剩下的背模板即可
#include2. 整数集合划分
![]()
#include 十三、多路归并
1. 三元组的最小距离(2020年全国硕士研究生招生考试)
![]()
![]()
什么是多路归并?
就是三个数组排序到一个数组进行比较
是需要开一个数组的空间的
为了节约空间,我们可以通过三个数组分别用三个指针
指向各自数组,然后判断当前三个元素的大小关系以及进行相应的运算或者应用数据去计算,之后根据三个元素的大小关系进行角标转移
放到本题中
首先我们要理解题意
题意是让我们求三个数组中放到一个数组排序后,出现的最小值到最大值距离最短的是多少
比如![]()
a b c之间满足
最小值a 到 最大值c距离最小
并且之间包含b数组的元素
或者是
b a c也可以
总之就是
最小值和最大值并且中间包含一个与这两个集合不一样的集合元素
的距离值 ✖ 2就是答案
#include 十四、摩尔投票法
1. 数组中出现次数超过一半的数字
![]()
class Solution {
public:
int moreThanHalfNum_Solution(vector<int>& nums) {
int cnt = 0, val;
for (auto x: nums) {
if (!cnt) val = x, cnt ++ ;
else if (x == val) cnt ++ ;
else cnt -- ;
}
return val;
}
};
十五、DFS
1. 全排列( 北京大学考研机试题 )
![]()
#include 2. 八皇后( 北京大学考研机试题 )
![]()
#include高精度计算核心就是
通过数组模拟出草稿纸上的运算过程
具体逻辑可以搜csdn
十六、模拟
1. 反序输出( 清华大学考研机试题 )
考点:reverse(s.begin(), s.end());
#include 2. 特殊乘法( 清华大学考研机试题 )
#include 3. 众数( 清华大学考研机试题 )
#include 4. 糖果分享游戏
#include十七、递推
1. 递推数列( 清华大学考研机试题 )
#include 2. 吃糖果( 北京大学考研机试题 )
#include十八、BFS
1. 玛雅人的密码
![]()
整体思路是用BFS暴搜
存在队列中的基本元素是pair
- 前者表示经过多次交换后当下的字符串的组成
- 后者表示达到当下的字符串状态,经过的交换次数
因为数字本身可能会重复出现,而且对于一个字符串交换它两个不同相邻位置得到的新字符串,也可能产生重复,但我们要求的是最少交换次数,因为BFS的性质,保证了可以实现最小,所以可以设置一个map映射组,来存储已经出现过的字符串情况,防止重复对相同组成的字符串再入队处理,以作到剪枝的作用,降低时间复杂度。
这道题进入BFS暴搜前,要做一些基本的判断,很容易就考虑不到,要做好了。
#include 2. 等差数列
![]()
本题的思路由样例入手
根据样例分析出
只要每行有两个元素
那么该行就能推出所有等差数据
同理列也是
所以我们先遍历所有行和列
看哪些有两个元素的
然后根据这样行和列进行填充
填充过程中观察是否新数据使得对应的行或者列
变得大于两个元素,进而可以填充
那么该过程就想到了bfs
bfs队列存储的元素是什么呢?就是所在的行或者列
怎么判断是行还是列呢?
行的范围为(0-n)
列的范围(n,m+n)
#include 十九、字符串处理
1. 首字母大写
![]()
#include 2. 日志排序
![]()
![]()
#include 3. 字符串转换整数
![]()
#include 二十、递归,画图
1. 重复者
![]()
本题由于第三次图形需要知道 第二层的图形
所以需要递归
#include 二十一、背包问题
1. 01背包
![]()
#include 2. 神奇的口袋( 体积恰好是 )
![]()
#include3. 整数拆分
![]()
本题中如果用这种做法的话会爆内存
#include#include 二十二、高精度
1. N的阶乘
![]()
做法:预处理
#include 2. 基本算术
![]()
#include 3. 整数查询
![]()
#include 二十三、因式分解
1. 质因数的个数
#include 2. 约数个数
#include 3. 阶乘的末尾0(上海交通大学考研机试题)
末尾的0 就表示 因数中有多少个10
那么也就是有多少个因数2 和 5
由于因数2的个数一定大于5的个数
所以就看有多少个因数5就可以了
#include 4. 整除问题(上海交通大学考研机试题)
#include 二十四、枚举
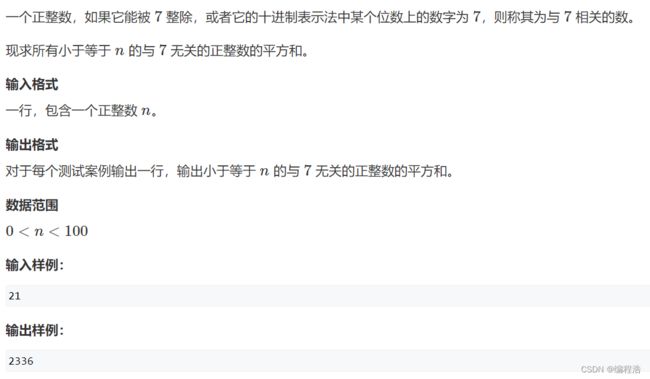
1. 与7无关的数 (北京大学考研机试题)
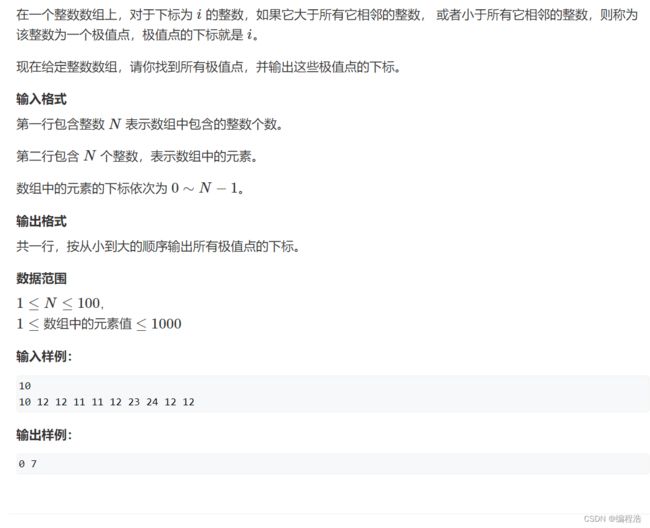
#include 2. 打印极值点下标( 北京大学考研机试题 )
#include 3. 最简真分数( 北京大学考研机试题 ) 【真分数】
- 分子大于分母
- 最大公约数是1
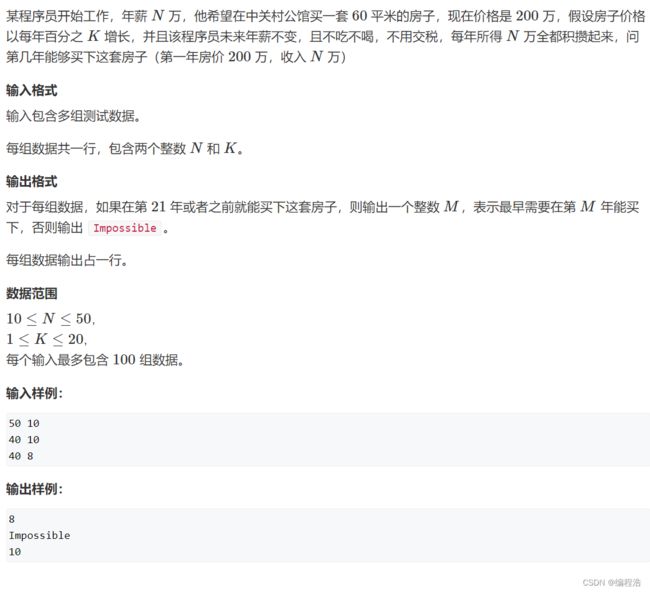
#include 4. 买房子 ( 北京大学考研机试题 )【算立方和平方】
include <iostream>
#include 5. Special数(北京邮电大学考研机试题)
#include 二十六、位运算
1. 位操作练习(北京大学考研机试题)
本题的思路是:
把a右移1位,如果超界,&65535(也就是保留16位)
然后让a + (a未移动的值右移15位的值)
得到的就是循环移动的值了
#include2. 二进制数(北京邮电大学考研机试题)
#include 二十七、矩阵
1. 旋转矩阵(北京航空航天大学考研机试题)
![]()
这道题就是找规律
![]()
#include 2. 矩阵幂【矩阵相乘】(北京邮电大学考研机试题)
![]()
两个矩阵相乘结果
两个矩阵a,b相乘得到一个新的矩阵c,新矩阵的第i行第j列的元素是a的第i行和b的第j列的对应元素相乘的求和。
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
tmp[i][j]+=a[i][k]*b[k][j];
求矩阵的k次方
注意:1次方就是 矩阵乘单位矩阵
#include 3. C翻转(北京邮电大学考研机试题)
![]()
#include 二十八、计算几何
1. 球的计算
![]()
#include 2. 点的距离
![]()
重新定义类的相减
#include 3. 直角三角形
![]()
#include 二十九、前缀和
1. 最长平衡串(北京邮电大学考研机试题)
![]()
![]()
#include 三十、推公式
1. 数字台阶
![]()
![]()
#include 2. 整数和
![]()
推等差公式
#include3. 弹地小球
![]()
#include 三十一、最短路
1. 我想回家(北京大学考研机试题)
![]()
求城市1到所属阵营城市的最短路径,记录在dist1[]中
求城市2到所属阵营城市的最短路径,记录在dist2[]中
遍历所有边,边的两端的城市i、j分别属于阵营1、2, 该边的权重为w
那么本题可以等价于求解:
min(w+dist[i]+dist[j])
#include 2. 最短路径
![]()
#include 3. 最短路径
![]()
#include 三十二、思维题
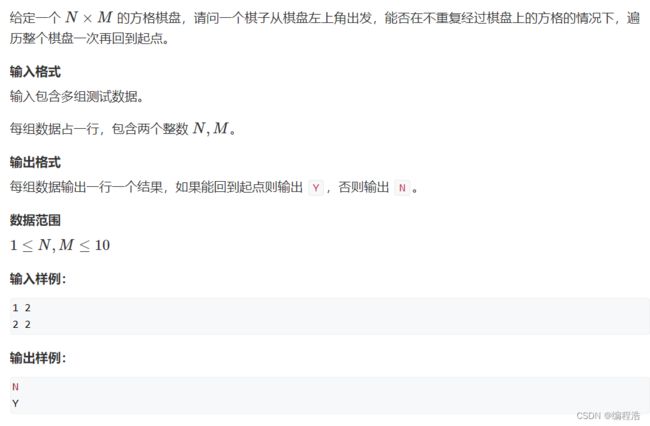
1. 棋盘遍历问题(上海交通大学考研机试题)
2.接着n1||m1时,但棋子走出去后,显然没有回头的路,答案应该是N
3.接着是n%2==0时,棋子可以先一直走到底,再把最后一行遍历完,再是倒数第二行,倒数第三…可以发现,棋子从倒数第一行开始的转向分别是右左右左右左右左…只要最后是向左,就可以遍历完,即n为偶数,答案为Y
示意图:
1 2 3
4 5 6
7 8 9
10 11 12
顺序依次为:1 4 7 10 11 12 9 8 5 6 3 2 1
4.然后是m%2==0时,棋子也是先走到底,再把第二列除去第一行的棋子遍历完,接着是第三,第四,第五列(都不遍历第一行)…最后再把第一行遍历了,即可到达终点,答案为Y
示意图:
1 2 3 4
5 6 7 8
9 10 11 12
顺序依次为:1 5 9 10 6 7 11 12 8 4 3 2 1
5.最后剩下的就是无解情况,答案为N
#include 三十三、哈希表
1. 子串计算(北京大学考研机试题)
map自动排序
#include 2. 查找(北京邮电大学考研机试题)
unordered_set(通过count(x)==0判断是否存在)
#include 3. 单词识别(北京理工大学考研机试题)
#include 三十四、双指针
1. 最小面积子矩阵
算法1:二维前缀和
#include 算法2:一维前缀和 + 双指针
#include 三十五、序列型DP
1. 最大序列和(清华大学考研机试题)

这道题目实际上就是求一串数字中,某一段数字和,使其最大
因此,我们可以使用dp来完成
令:dp[i]为以a[i]结尾的最大序列和
则dp[i]可以为 以a[i-1]结尾的最大序列和加上a[i] 与 a[i]中的最大值
即该题的动态转移方程式可以为:dp[i]=max(dp[i-1]+a[i],dp[i]);
#include 2. 最长ZigZag子序列
#include 三十六、红黑树和并查集
1. 合并集合
![]()
#include