【Matlab】BP神经网络遗传算法(BP-GA)函数极值寻优——非线性函数求极值

目前关于神经网络遗传算法函数极值寻优——非线性函数求极值的博客资源已经不少了，我看了下来源，最初的应该是来自于Matlab中文论坛，论坛出版的《MATLAB神经网络30个案例分析》第4章就是《神经网络遗传算法函数极值寻优——非线性函数极值寻优》。
【简书】神经网络遗传算法函数极值寻优
【博客网】MATLAB神经网络（4） 神经网络遗传算法函数极值寻优——非线性函数极值寻优

参考前人的文章资源，本篇博客将对神经网络遗传算法函数极值寻优进行解析，说明代码使用方法。

1.背景条件

要求：对于未知模型（函数表达式未知）求解极值。
条件：已知模型的一些输入输出数据。

程序的示例是根据用神经网络遗传算法寻优非线性函数 $y=x_1^2+x_2^2$ 的极值，输入参数有2个，输出参数有1个，易知函数有极小值0，极小值点为(0, 0)。已知的只有一些输入输出数据（用rand函数生成输入，然后代入表达式生成输出）：

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=input(i,1)^2+input(i,2)^2;
end

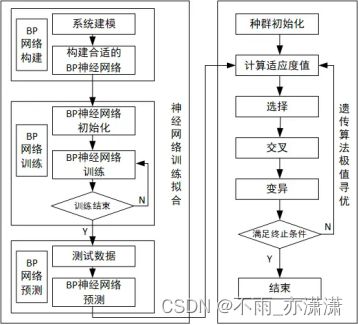
2.算法框架

对于未知的非线性函数，仅通过函数的输入输出数据难以准确寻找函数极值。这类问题可以通过神经网络结合遗传算法求解，利用神经网络的非线性拟合能力和遗传算法的非线性寻优能力寻找函数极值。

3.BP神经网络函数说明

newff

BP神经网络参数设置函数
函数形式：

net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)

P:输入数据矩阵。
T:输出数据矩阵。
S:隐含层节点数。

例如：

net=newff(inputn,outputn,15); % 单隐含层BP神经网络，隐含层的节点数是15

通过配置S向量，可以方便地得到包含多个隐含层的BP神经网络，如下面语句：

net=newff(inputn, outputn, [5,5]); % 双隐含层BP神经网络，每个隐含层的节点数都是5

train

BP神经网络训练函数
函数形式：

[net, tr] = train(NET, X, T, Pi, Ai)

NET:待训练网络。
X:输入数据矩阵。
T:输出数据矩阵。

例如：

net=train(net,inputn,outputn);

sim

BP神经网络预测函数
函数形式：

y=sim(net, x)

net :训练好的网络。
x:输入数据。

例如：

an=sim(net,inputn_test);

4.完整代码

data.m

用于生成神经网络拟合的原始数据。

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=input(i,1)^2+input(i,2)^2;
end
output=output';

save data input output

BP.m

用函数输入输出数据训练BP神经网络，使训练后的网络能够拟合非线性函数输出，保存训练好的网络用于计算个体适应度值。根据非线性函数方程随机得到该函数的4000组输入输出数据，存储于data中，其中input为函数输入数据，output为函数对应输出数据，从中随机抽取3900组训练数据训练网络，100组测试数据测试网络拟合性能。最后保存训练好的网络。

%% 清空环境变量
clc
%clear

tic
%% 训练数据预测数据提取及归一化
%加载输入输出数据
load data input output

%从1到4000间随机排序
k=rand(1,4000);
[m,n]=sort(k);

%找出训练数据和预测数据
input_train=input(n(1:3900),:)';
output_train=output(n(1:3900),:)';
input_test=input(n(3901:4000),:)';
output_test=output(n(3901:4000),:)';

%训练样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);

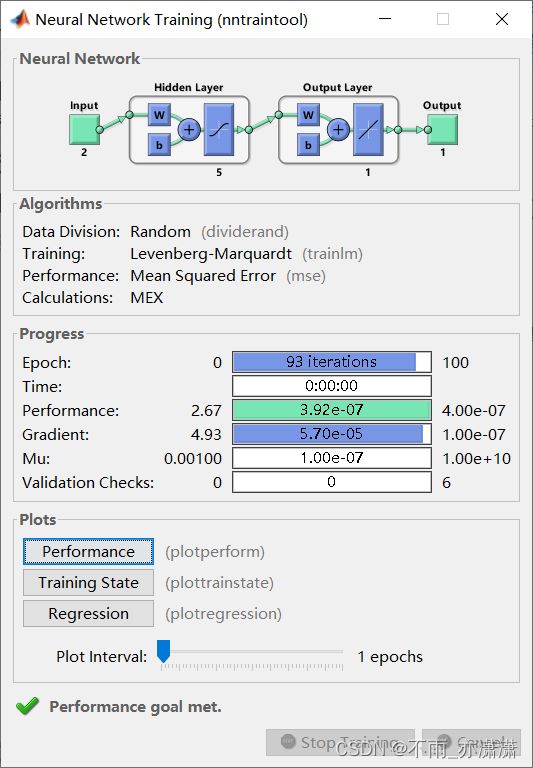
%% BP网络训练
% %初始化网络结构
net=newff(inputn,outputn,5);

% 设置网络参数：迭代次数、学习率和目标
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0000004;

%网络训练
net=train(net,inputn,outputn);

%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
 
%网络预测输出
an=sim(net,inputn_test);
 
%网络输出反归一化
BPoutput=mapminmax('reverse',an,outputps);

%% 结果分析

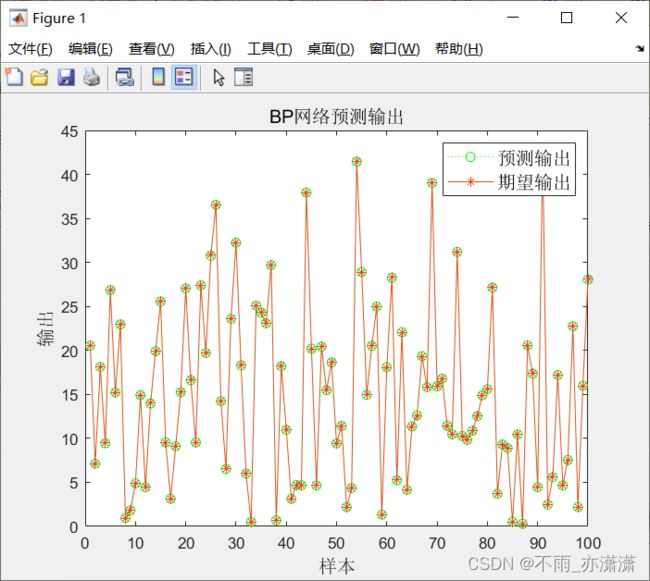
figure(1)
plot(BPoutput,':og')
hold on
plot(output_test,'-*');
legend('预测输出','期望输出','fontsize',12)
title('BP网络预测输出','fontsize',12)
xlabel('样本','fontsize',12)
ylabel('输出','fontsize',12)
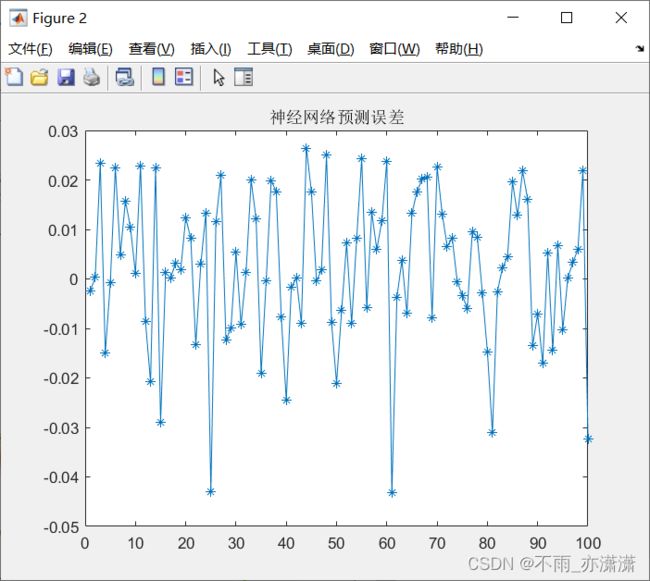
%预测误差
error=BPoutput-output_test;

figure(2)
plot(error,'-*')
title('神经网络预测误差')

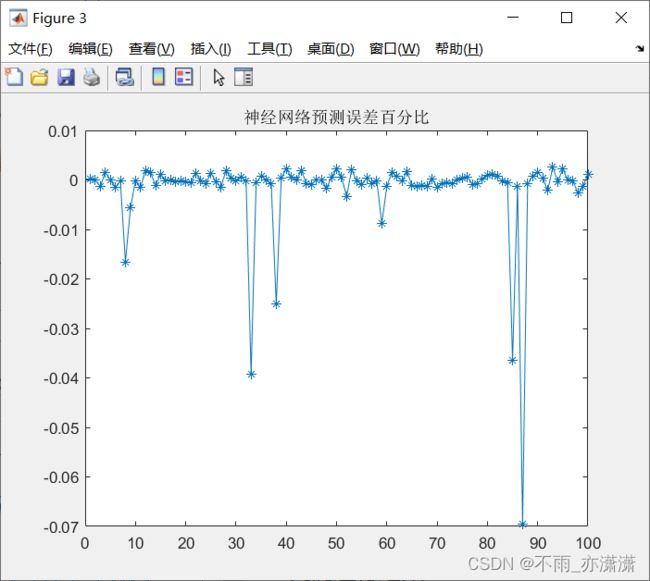
figure(3)
plot((output_test-BPoutput)./BPoutput,'-*');
title('神经网络预测误差百分比')

errorsum=sum(abs(error))

toc

save data net inputps outputps

Code.m

编码成染色体。

function ret=Code(lenchrom,bound)
%本函数将变量编码成染色体，用于随机初始化一个种群
% lenchrom   input : 染色体长度
% bound      input : 变量的取值范围
% ret        output: 染色体的编码值
flag=0;
while flag==0
    pick=rand(1,length(lenchrom));
    ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick; %线性插值，编码结果以实数向量存入ret中
    flag=test(lenchrom,bound,ret);     %检验染色体的可行性
end

fun.m

把训练好的BP神经网络预测输出作为个体适应度值。

function fitness = fun(x)
% 函数功能：计算该个体对应适应度值
% x           input     个体
% fitness     output    个体适应度值

%
load data net inputps outputps

%数据归一化
x=x';
inputn_test=mapminmax('apply',x,inputps);
 
%网络预测输出
an=sim(net,inputn_test);
 
%网络输出反归一化
fitness=mapminmax('reverse',an,outputps);

对于求极小值的函数，适应度可以设为BP网络预测结果，如果需要求极大值，可以对适应度取反。

Select.m

选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。

function ret=select(individuals,sizepop)
% 本函数对每一代种群中的染色体进行选择，以进行后面的交叉和变异
% individuals input  : 种群信息
% sizepop     input  : 种群规模
% ret         output : 经过选择后的种群

fitness1=1./individuals.fitness;
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;
index=[]; 
for i=1:sizepop   %转sizepop次轮盘
    pick=rand;
    while pick==0    
        pick=rand;        
    end
    for i=1:sizepop    
        pick=pick-sumf(i);        
        if pick<0        
            index=[index i];            
            break;  %寻找落入的区间，此次转轮盘选中了染色体i，注意：在转sizepop次轮盘的过程中，有可能会重复选择某些染色体
        end
    end
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;

Cross.m

交叉操作从种群中选择两个个体，按一定概率交叉得到新个体。

function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss                input  : 交叉概率
% lenchrom              input  : 染色体的长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% ret                   output : 交叉后的染色体
 for i=1:sizepop  %每一轮for循环中，可能会进行一次交叉操作，染色体是随机选择的，交叉位置也是随机选择的，%但该轮for循环中是否进行交叉操作则由交叉概率决定（continue控制）
     % 随机选择两个染色体进行交叉
     pick=rand(1,2);
     while prod(pick)==0
         pick=rand(1,2);
     end
     index=ceil(pick.*sizepop);
     % 交叉概率决定是否进行交叉
     pick=rand;
     while pick==0
         pick=rand;
     end
     if pick>pcross
         continue;
     end
     flag=0;
     while flag==0
         % 随机选择交叉位
         pick=rand;
         while pick==0
             pick=rand;
         end
         pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置，即选择第几个变量进行交叉，注意：两个染色体交叉的位置相同
         pick=rand; %交叉开始
         v1=chrom(index(1),pos);
         v2=chrom(index(2),pos);
         chrom(index(1),pos)=pick*v2+(1-pick)*v1;
         chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
         flag1=test(lenchrom,bound,chrom(index(1),:));  %检验染色体1的可行性
         flag2=test(lenchrom,bound,chrom(index(2),:));  %检验染色体2的可行性
         if   flag1*flag2==0
             flag=0;
         else flag=1;
         end    %如果两个染色体不是都可行，则重新交叉
     end
 end
ret=chrom;

test.m

检验染色体的可行性。

function flag=test(lenchrom,bound,code)
% lenchrom   input : 染色体长度
% bound      input : 变量的取值范围
% code       output: 染色体的编码值

x=code; %先解码
flag=1;
if (x(1)<bound(1,1))&&(x(2)<bound(2,1))&&(x(1)>bound(1,2))&&(x(2)>bound(2,2))
    flag=0;
end

Mutation.m

变异操作从种群中随机选择一个个体，按一定概率变异得到新个体。

function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
% 本函数完成变异操作
% pcorss                input  : 变异概率
% lenchrom              input  : 染色体长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% opts                  input  : 变异方法的选择
% pop                   input  : 当前种群的进化代数和最大的进化代数信息
% ret                   output : 变异后的染色体
for i=1:sizepop   %每一轮for循环中，可能会进行一次变异操作，染色体是随机选择的，变异位置也是随机选择的，
    %但该轮for循环中是否进行变异操作则由变异概率决定（continue控制）
    % 随机选择一个染色体进行变异
    pick=rand;
    while pick==0
        pick=rand;
    end
    index=ceil(pick*sizepop);
    % 变异概率决定该轮循环是否进行变异
    pick=rand;
    if pick>pmutation
        continue;
    end
    flag=0;
    while flag==0
        % 变异位置
        pick=rand;
        while pick==0      
            pick=rand;
        end
        pos=ceil(pick*sum(lenchrom));  %随机选择了染色体变异的位置，即选择了第pos个变量进行变异
        v=chrom(i,pos);        
        v1=v-bound(pos,1);        
        v2=bound(pos,2)-v;        
        pick=rand; %变异开始        
        if pick>0.5
            delta=v2*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v+delta;
        else
            delta=v1*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v-delta;
        end   %变异结束
        flag=test(lenchrom,bound,chrom(i,:));     %检验染色体的可行性
    end
end
ret=chrom;

主函数 Genetic.m

%% 清空环境变量
clc
% clear

%% 初始化遗传算法参数
%初始化参数
maxgen=100;                         %进化代数，即迭代次数
sizepop=20;                        %种群规模
pcross=[0.4];                       %交叉概率选择，0和1之间
pmutation=[0.2];                    %变异概率选择，0和1之间

lenchrom=[1 1];          %每个变量的字串长度，如果是浮点变量，则长度都为1
bound=[-5 5;-5 5];  %数据范围

individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness=[];                      %每一代种群的平均适应度
bestfitness=[];                     %每一代种群的最佳适应度
bestchrom=[];                       %适应度最好的染色体

%% 初始化种群计算适应度值
% 初始化种群
for i=1:sizepop
    %随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound);   
    x=individuals.chrom(i,:);
    %计算适应度
    individuals.fitness(i)=fun(x);   %染色体的适应度
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:);  %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness]; 

%% 迭代寻优
% 进化开始
for i=1:maxgen
    i
    % 选择
    individuals=Select(individuals,sizepop); 
    avgfitness=sum(individuals.fitness)/sizepop;
    % 交叉
    individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
    
    % 计算适应度 
    for j=1:sizepop
        x=individuals.chrom(j,:); %解码
        individuals.fitness(j)=fun(x);   
    end
    
  %找到最小和最大适应度的染色体及它们在种群中的位置
    [newbestfitness,newbestindex]=min(individuals.fitness);
    [worestfitness,worestindex]=max(individuals.fitness);
    % 代替上一次进化中最好的染色体
    if bestfitness>newbestfitness
        bestfitness=newbestfitness;
        bestchrom=individuals.chrom(newbestindex,:);
    end
    individuals.chrom(worestindex,:)=bestchrom;
    individuals.fitness(worestindex)=bestfitness;
    
    avgfitness=sum(individuals.fitness)/sizepop;
    
    trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束

%% 结果分析
[r c]=size(trace);
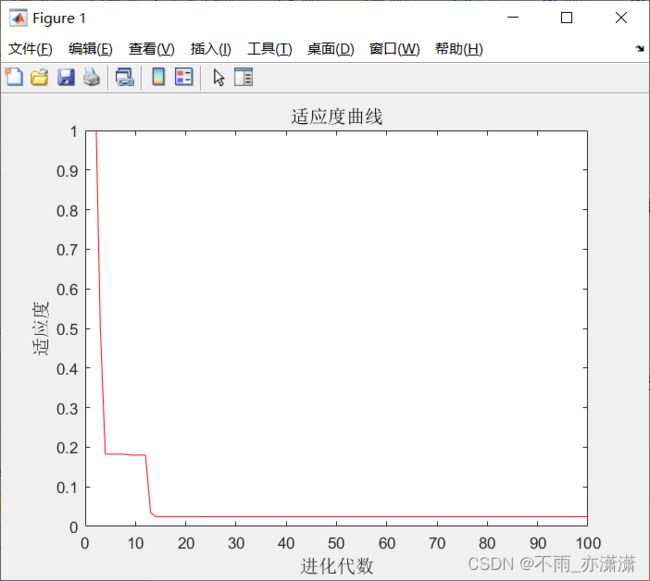
plot([1:r]',trace(:,2),'r-');
title('适应度曲线','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
axis([0,100,0,1])
disp('适应度                   变量');
x=bestchrom;
% 窗口显示
disp([bestfitness x]);

5.代码使用说明

上述代码运行顺序

data.m 生成数据（如果已有 input output 数据可跳过），
BP.m 进行BP神经网络训练及函数拟合，
Genetic.m（主函数）利用遗传算法求极值。

求最大值的方法

上述代码用于求解最小值，对于求解最大值的需求，可以在适应度函数里面，对适应度计算结果求反，把求解最大值的问题转化为求解最小值的问题。

例如：对于非线性函数 $y=-(x_1^2+x_2^2)+4$ ：

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=-(input(i,1)^2+input(i,2)^2)+4;
end

求最大值时，需要在 fun.m 里面，修改最后一行代码：

fitness=-mapminmax('reverse',an,outputps);

最终运行找到的极值点为（0.4714， -0.0319），适应度为-3.7554，极值需要对适应度取反，为3.7554。

注意：每次运行结果不尽相同。

6.代码运行结果

对 $y=x_1^2+x_2^2$ 求极小值

BP神经网络拟合

运行BP.m之后：

输出：

errorsum =

    1.2004

历时 1.386858 秒。

注意：每次运行结果不尽相同。

遗传算法寻优

运行主函数 Genetic.m之后：

输出：

...
i =

   100

适应度                   变量
    0.0247    0.0001    0.0001

最终结果最优个体为（0.0001，0.0001），适应度为0.0247，与实际最小值点（0，0）和最小值0已经很接近了。

注意：每次运行结果不尽相同。

参考

【知乎】遗传算法基础、MATLAB的遗传算法（工具箱实现）