二分法的应用
文章目录
- 什么是二分法
- 二分查找的优先级
- 二分查找的步骤
-
- 图解演示
- 代码演示
-
- python程序实现⬛
- C程序实现
- C++程序实现
- Java程序实现
- 非常规类二分查找
-
- 查找有序列表中某数首次出现的位置
什么是二分法
二分法(Bisection method),即一分为二的的方法。数学的零点估计问题中:对于在区间[a,b]上连续不断且满足 f(a) * f(b) <0的函数y=f(x),通过不断地把函数f(x)的零点所在区间二等分,使区间两个端点逐步逼近零点,进而得到零点的近似值的方法。
当然,在我们技术人的手中,一般是用来解决有序列表中查找某个元素的问题,属于搜索方法的一种。
简单的来说,就是将答案所在的区间不断缩小为原来的 1/2,直到找到答案。
类似二分法的实例
假如你和朋友在玩猜数字游戏,朋友记录一个数,规定数的范围,你来猜。你每猜一个数,朋友会告诉你这个数大了还是小了,直到你猜出正确答案为止。假如有100个数,你一个一个数猜,你最差的情况需要找100次,如果你使用二分的思想查找,每次折半,最多只需要7次即可猜出答案。
二分查找的优先级
二分查找算法的时间复杂度为O(log n),因此其优先级较高,适合在需要快速查找有序列表中的元素时使用。相比于线性查找算法的时间复杂度为O(n),二分查找算法具有更高的效率,尤其适用于数据量较大的情况。同时,二分查找算法较为简单,易于实现和理解,因此被广泛应用于各个领域的程序设计中。
二分查找的效率虽然高,但只局限于有序列表
二分查找的步骤
二分查找的思路是先取中间位置的值进行比较,如果该值等于目标值,则查找成功;否则,如果该值大于目标值,则在左半部分继续查找;如果该值小于目标值,则在右半部分继续查找。不断重复以上步骤,直到找到目标值或者确定目标值不存在为止。
图解演示
在下面这个有序数组中查找数字3
定义三个指针:left、right、mid
这三个指针都是动态的,left 为左边界的下标,right 为右边界的下标,mid=(left+right)/2

arr[mid]>3,中间值大于目标值,说明右边没有要查找的数,之后范围缩小到左边。
改变右指针right=mid-1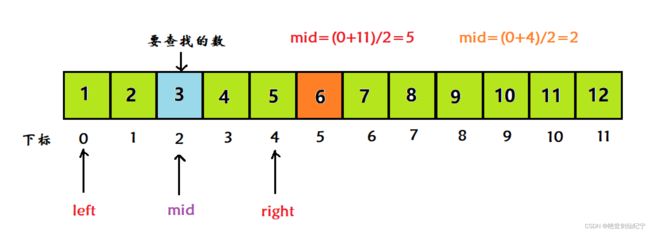
这里 arr[mid] 恰好等于要查找的数,二分结束。
假设要查找的数变为4,那么还需要继续查找,如图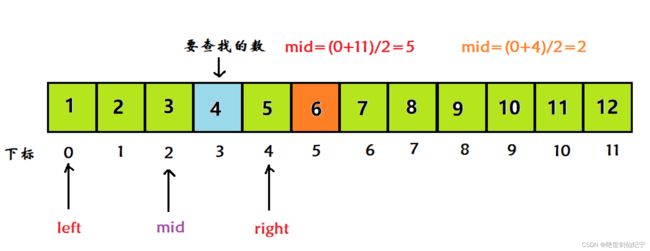
arr[mid]<4,中间值小于目标值,说明左边没有要查找的数,范围再缩小到原来的右边
改变左指针left=mid+1

arr[mid]=4 就找到了需要查找的数
当左指针 left 大于等于右指针 right 时,二分查找结束,答案可能是找到目标值或者目标值不存在。
代码演示
其中,arr为有序列表,target为需要查找的元素,最终未找到就返回 -1
python程序实现⬛
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
定义一个函数binary_search,该函数接受两个参数:一个有序数组 arr 和要查找的目标元素 target
C程序实现
#include 自己定义一个函数binary_search,接收数组、数组的左右边界下标(或数组元素个数),以及要查找的元素
C++程序实现
#include 函数binarySearch为二分查找函数,该函数接受一个整数数组,数组的左右边界以及要查找的元素
Java程序实现
public class BinarySearch {
int binarySearch(int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2;
if (arr[mid] == x) {
return mid;
}
if (arr[mid] > x) {
return binarySearch(arr, l, mid - 1, x);
}
return binarySearch(arr, mid + 1, r, x);
}
return -1;
}
public static void main(String args[]) {
BinarySearch bs = new BinarySearch();
int arr[] = { 2, 4, 6, 8, 10 };
int n = arr.length;
int x = 8;
int result = bs.binarySearch(arr, 0, n - 1, x);
if (result == -1) {
System.out.println("Element not found");
}
else {
System.out.println("Element found at index " + result);
}
}
}
在此示例中定义了一个类BinarySearch,其中包含一个递归函数binarySearch,该函数接受一个整数数组,数组的左右边界以及要查找的元素。
非常规类二分查找
查找有序列表中某数首次出现的位置
如下图中,找到3首次出现的位置(左边界),不难。但要以时间复杂度为 log(N)找到,就要采用二分查找了。

C程序代码
int Find_Edges(int*nums,int len,double k)
{
int left=0,right=len-1;
while(left<=right)
{
int mid=(left+right)/2;
if(nums[mid]<k)
left=mid+1;
else if(nums[mid]>k)
right=mid-1;
}
return left;
}
int GetNumberOfK(int* nums, int numsLen, int k ) {
return Find_Edges(nums,numsLen,k-0,5);
}
上面这段代码将参数 3-0.5 传上去,就可以求出3的左边界,因为传上去的是浮点数,那肯定是找不到的,只能找到距离最近的向上取整的可以找到的数,因为整数除法是向下取整的,所以,mid的值一定是小于等于 (left+right)/2的,所以一定会在 left 位置结束二分查找。
同样,将参数 3+0.5 传上去,就可以求出3的右边界,进而求出这个数组中一共有多少个3,进而解决这篇博客中最后一题C语言笔试训练。
