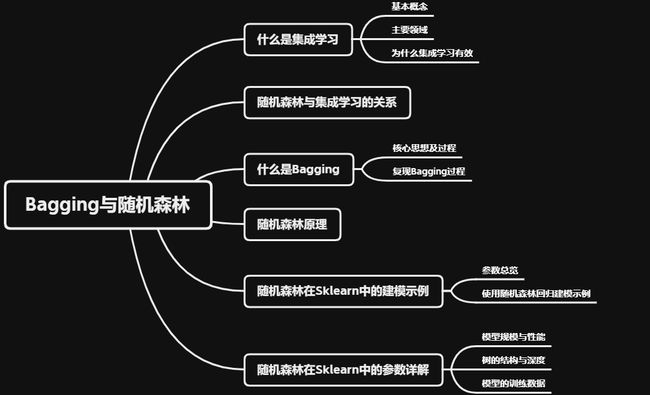
机器学习(十八):Bagging和随机森林
全文共10000余字,预计阅读时间约30~40分钟 | 满满干货(附数据及代码),建议收藏!
本文目标:理解什么是集成学习,明确Bagging算法的过程,熟悉随机森林算法的原理及其在Sklearn中的各参数定义和使用方法
代码及数据集下载点这里
一、引言
在机器学习的众多算法中,随机森林无疑是其中最受欢迎和最经常被应用的方法之一。在机器学习竞赛当中,随机森林往往是在中小型数据上尝试的第一个算法,随机森林算法构筑过程非常简单,可以说如果掌握了决策树的各项属性和参数,随机森林的大部分内容都相当容易理解,如果还不太熟悉的,建议先看看这两篇文章:
机器学习(十六):决策树
机器学习(十七):实操_在Sklearn中的实现CART树的基本流程
但是在深入了解随机森林之前,要先搞懂集成学习的相关概念,原因是随机森林并不是一个孤立存在的算法,而是集成学习方法中的一个典型代表。要真正理解随机森林的工作原理、优势与局限性,必须首先理解它背后的集成学习框架。正如一栋大厦的稳固性不仅仅来自其基石,而是整体结构的合理组合,随机森林的强大之处也在于其将多棵决策树的力量集结起来,形成一个更为强大、稳健的预测模型。
二、什么是集成学习
2.1 基本概念
所谓的集成学习,其本质上是机器学习中的一种策略,通过组合多个学习算法或模型来进行决策或预测,是机器学习中最先进、最有效、最具研究价值的领域之一,这类方法会训练多个弱评估器(base estimators)、并将它们输出的结果以某种方式结合起来解决一个问题。所以其基本思想是组合多个弱学习器形成一个强学习器,最终通过综合多个模型的输出,获得比单一模型更好的泛化性能。
从目前的工业场景视角来看,集成学习的应用也是非常广泛,在Kaggle、天池等数据竞赛中它作为御用算法总是能提供较高的竞赛分数,在搜索、推荐、广告等众多领域,它能作为工业标准和基准模型,它也是目前唯一能与深度学习算法分庭抗礼的算法,所以掌握其原理和使用,是非常有必要的。
如果通俗的理解集成学习算法:想象你要做一个重要的决策,比如购买一辆新车。你可能会询问多位朋友或家人的意见,因为每个人可能会从不同的角度为你提供建议。有的人可能更关注车辆的燃油效率,有的人可能更看重车的舒适性,而有的人可能考虑价格。通过综合这些不同的意见,你能够做出一个更全面和更明智的决策。
集成学习就是这个道理。它并不依赖于单一的模型来做出预测,而是询问多个模型(就像多位朋友)并结合它们的答案。这样,就能得到一个更准确、更稳定的答案,因为这种方法利用了多个模型的"集体智慧"。
2.2 主要领域
在集成学习的发展历程中,集成的思想以及方法启发了众多深度学习和机器学习方面的工作,在学术界和工业界都取得了巨大的成功。总的来说集成学习可以被分为三个主要研究领域:
- 模型融合
模型融合在最初的时候被称为“分类器结合”,这个领域主要关注强评估器,试图设计出强大的规则来融合强分类器的结果、以获取更好的融合结果。这个领域的手段主要包括了投票法Voting、堆叠法Stacking、混合法Blending等,且被融合的模型需要是强分类器。模型融合技巧是机器学习/深度学习竞赛中最为可靠的提分手段之一,常言道:当你做了一切尝试都无效,试试模型融合。 - 弱分类器集成
弱分类器集成主要专注于对传统机器学习算法的集成,这个领域覆盖了大部分熟悉的集成算法和集成手段,如装袋法bagging,提升法boosting。这个领域试图设计强大的集成算法、来将多个弱学习器提升成为强学习器。 - 混合专家模型
混合专家模型常常出现在深度学习(神经网络)的领域。在其他集成领域当中,不同的学习器是针对同一任务、甚至在同一数据上进行训练,但在混合专家模型中,是将一个复杂的任务拆解成几个相对简单且更小的子任务,然后针对不同的子任务训练个体学习器(专家),然后再结合这些个体学习器的结果得出最终的输出。
2.3 为什么集成学习有效
集成学习之所以通常很有效,是因为它结合了多个模型的预测以产生一个最终的预测。这种方法的效果好是基于以下几个原因:
如果您还不太清楚方差、偏差和误差相关的概念,建议您先看下这篇文章:
机器学习(七): Bias、Error和Variance的区别与联系
但值得注意的是,虽然集成学习在很多场景下都很有效,但它并不是一个银弹。在某些情况下,单个模型可能与集成模型的性能相当或更好。此外,集成方法也会增加计算负担,因为需要训练和预测多个模型。因此,使用集成方法时应权衡性能提升与计算成本之间的关系。
三、随机森林与集成学习的关系
上面提到了集成学习主要有三个研究领域,分别是模型融合、弱分类器集成和混合专家模型,随机森林位于弱分类器集成的子领域内。
弱分类器集成重点研究如何将多个性能略低于随机猜测(或稍好一点)的模型(即弱学习器)集成为一个性能更强、更稳定的模型。其中,装袋法(Bagging)和提升法(Boosting)是这个子领域的两大核心技术。
随机森林,具体地说,是装袋法(Bagging)的一个扩展,是基于决策树的Bagging方法的具体实现。它不仅仅是简单地通过自助抽样(bootstrap sampling)进行样本集的随机抽取,而是在此基础上进一步引入了特征的随机选择,为构建的每棵决策树提供不同的特征子集。增强模型的多样性并减少了过拟合的风险。
因此,随机森林与集成学习的关系可以概括为:随机森林是弱分类器集成技术中,基于装袋法并对其进行扩展、并以决策树为基学习器的一种特定算法。
四、什么是Bagging
4.1 核心思想及过程
Bagging是“Bootstrap Aggregating”的缩写,是一种集成学习技术,具体来说是一种弱分类器集成方法。引用Leo Breiman[1996年]的一篇论文“bagging Predictors”,Leo将Bagging描述为:“Bagging predictors是一种生成一个预测器的多个版本并使用这些版本来获得一个聚合预测器的方法”,其核心思想和步骤如下:
- Step 1:Bootstrap抽样
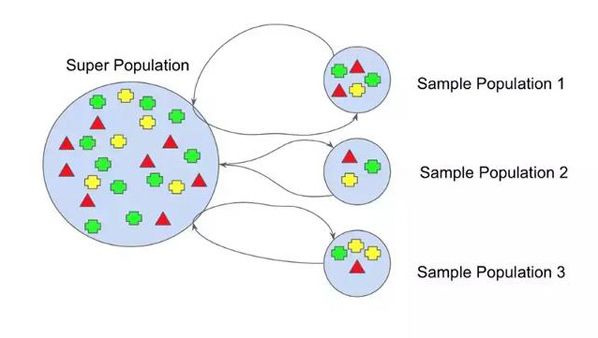
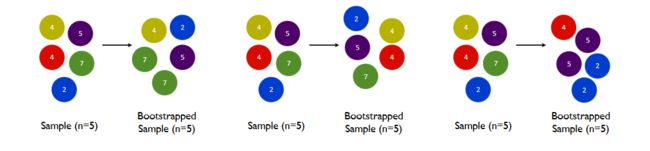
Bagging的核心是通过有放回地随机抽样技术(也称为Bootstrap抽样)从训练数据集中重复地抽取子集。因此,每一次抽样可能会得到不完全相同的数据子集。
在机器学习中,bootstrap方法是指随机抽样和替换,这种样本称为重采样。在Bagging中,Bootstrap抽样被用来创建多个不同的训练数据子集,进而训练多个模型,这个过程需要重点关注以下几个细节:
- 数据集大小的确定:在Bagging中,通常选择的样本数与原始数据集的大小相同。
- 有放回的随机抽样:样本在被选中后不会被从原始数据集中移除,这意味着它在后续的抽样中仍然可能被再次选中。
- 重复抽样:重复上述的随机抽样过程,直到新的数据子集达到预定的大小(通常与原始数据集大小相同).
- 多次抽样:为了在Bagging中训练多个模型,需要重复整个Bootstrap抽样过程多次,从而生成多个数据子集。
如上图,其中每个样本总体都有不同的部分,而且没有一个是相同的。
- Step 2:独立训练
使用每个数据子集来独立训练一个学习模型(例如,决策树、神经网络等)。由于这些模型是在不同的数据子集上训练的,每个模型的偏见和方差都会有所不同。
- Step 3:模型聚合
在Bagging集成当中,并行建立多个弱评估器(通常是决策树,也可以是其他非线性算法),并综合多个弱评估器的结果进行输出。当集成算法目标是回归任务时,集成算法的输出结果是弱评估器输出的结果的平均值,当集成算法的目标是分类任务时,集成算法的输出结果是弱评估器输出的结果少数服从多数。
4.2 复现Bagging过程
复现一下上述Bagging的过程:假设现在一个bagging集成算法当中有9个弱评估器,代码如下:
- Step 1:准备模拟数据并进行Bootstrap抽样
# 创建一个简单的数据集
X, y = make_classification(n_samples=100, n_features=20, random_state=42)
# 设置Bagging参数
n_estimators = 9
# 细节1:在Bagging中,通常选择的样本数与原始数据集的大小相同
subset_size = len(X)
weak_learners = []
# Step 1:Bootstrap抽样
print("Step 1: Bootstrap sampling\n")
for i in range(n_estimators):
# 细节2:有放回的随机抽样,参数 replace=True 指示这是一个有放回的抽样
bootstrap_indices = np.random.choice(np.arange(X.shape[0]), size=subset_size, replace=True)
X_bootstrap = X[bootstrap_indices]
y_bootstrap = y[bootstrap_indices]
print(f"Bootstrap sample {i + 1} contains {len(np.unique(bootstrap_indices))} unique instances out of {subset_size}.")
# 打印每次抽取的X_bootstrap和y_bootstrap
print(f"X_bootstrap {i + 1}:")
print(X_bootstrap)
print(f"y_bootstrap {i + 1}:")
print(y_bootstrap)
print('-' * 75) # 分隔线,方便查看每个bootstrap样本的输出
看一下抽样结果:
仅从前两个就可以看出每个样本是不同的,还有一个关键的点要解释一下,看下图:
Step 2:独立训练对测试集预测
for i in range(n_estimators):
# 细节2:有放回的随机抽样,参数 replace=True 指示这是一个有放回的抽样
bootstrap_indices = np.random.choice(np.arange(X.shape[0]), size=subset_size, replace=True)
X_bootstrap = X[bootstrap_indices]
y_bootstrap = y[bootstrap_indices]
print(f"Bootstrap sample {i + 1} contains {len(np.unique(bootstrap_indices))} unique instances out of {subset_size}.")
# Step 2:独立训练
tree = DecisionTreeClassifier()
tree.fit(X_bootstrap, y_bootstrap)
weak_learners.append(tree)
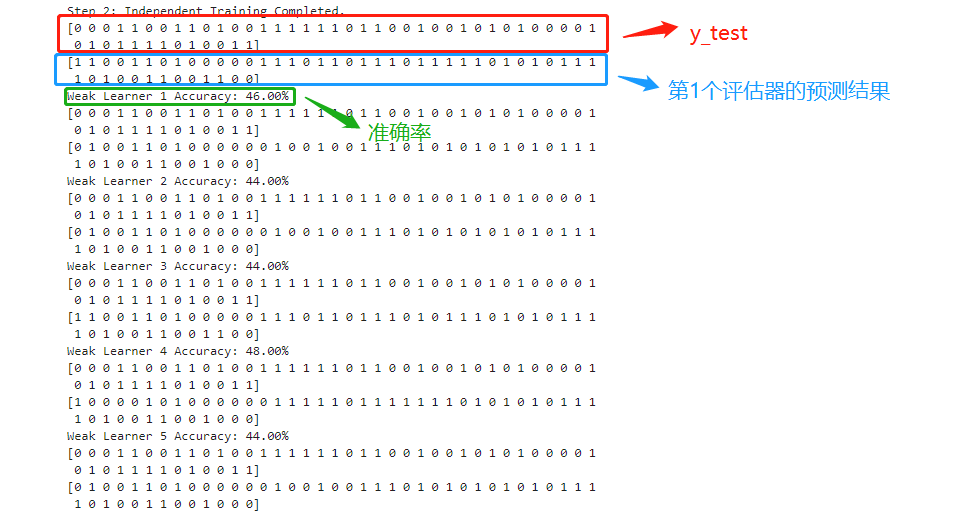
print("\nStep 2: Independent Training Completed.")
# 对于新的数据X_test进行预测
X_test, y_test = make_classification(n_samples=50, n_features=20, random_state=24)
predictions = []
for i, tree in enumerate(weak_learners):
print(y_test)
pred = tree.predict(X_test)
print(pred)
predictions.append(pred)
# 打印每个weak_learner的准确率
print(f"Weak Learner {i + 1} Accuracy: {accuracy_score(y_test, pred)*100:.2f}%")
看下输出结果:
9个不同的抽样数据集,会训练9个独立的评估器,在对同一个测试机y_test下也会得到不同的预测结果。
Step 3:模型聚合
模型聚合在Bagging中是通过少数服从多数来进行的。对于分类问题,每个模型给出其预测结果,然后选择最常见的预测结果作为最终输出。对于回归问题,则是通过取所有模型预测结果的平均值来得到最终输出。此示例是分类问题,所以使用了多数投票(Majority Voting)策略。对于每个测试样本,查看所有弱评估器的预测,然后选择得到最多投票的类别作为最终的预测。
# Step 3:模型聚合
final_predictions = [Counter(row).most_common(1)[0][0] for row in predictions]
print("\nStep 3: Model Aggregation")
print(f"Aggregated Prediction Accuracy: {accuracy_score(y_test, final_predictions)*100:.2f}%")
print("\nIn model aggregation for classification tasks in Bagging, the predictions from all the weak learners are combined, and the final output is the class that gets the most votes among all weak learners.")
看下输出:
结果表明,经过所有弱学习器的投票聚合后,Bagging集成的最终预测在测试数据集上的正确率是44%。换句话说,它正确地预测了44%的测试样本。
此代码只是为了演示手动模拟Bagging过程。在实际应用中,可以直接使用scikit-learn的BaggingClassifier或BaggingRegressor,它们已经高效地实现了这个过程。全部代码如下:
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score
from collections import Counter
# 创建一个简单的数据集
X, y = make_classification(n_samples=100, n_features=20, random_state=42)
# 设置Bagging参数
n_estimators = 9
# 细节1:在Bagging中,通常选择的样本数与原始数据集的大小相同
subset_size = len(X)
weak_learners = []
# Step 1:Bootstrap抽样
print("Step 1: Bootstrap sampling\n")
for i in range(n_estimators):
# 细节2:有放回的随机抽样,参数 replace=True 指示这是一个有放回的抽样
bootstrap_indices = np.random.choice(np.arange(X.shape[0]), size=subset_size, replace=True)
X_bootstrap = X[bootstrap_indices]
y_bootstrap = y[bootstrap_indices]
print(f"Bootstrap sample {i + 1} contains {len(np.unique(bootstrap_indices))} unique instances out of {subset_size}.")
# Step 2:独立训练
tree = DecisionTreeClassifier()
tree.fit(X_bootstrap, y_bootstrap)
weak_learners.append(tree)
print("\nStep 2: Independent Training Completed.")
# 对于新的数据X_test进行预测
X_test, y_test = make_classification(n_samples=50, n_features=20, random_state=24)
predictions = []
for i, tree in enumerate(weak_learners):
pred = tree.predict(X_test)
predictions.append(pred)
# 打印每个weak_learner的准确率
print(f"Weak Learner {i + 1} Accuracy: {accuracy_score(y_test, pred)*100:.2f}%")
predictions = np.array(predictions).T
# 打印每个weak_learner的预测结果
print("\nPredictions from each weak learner:")
for i, pred in enumerate(predictions):
print(f"Weak Learner {i + 1}:")
print(pred, "\n")
# Step 3:模型聚合
final_predictions = [Counter(row).most_common(1)[0][0] for row in predictions]
print("\nStep 3: Model Aggregation")
print(f"Aggregated Prediction Accuracy: {accuracy_score(y_test, final_predictions)*100:.2f}%")
print("\nIn model aggregation for classification tasks in Bagging, the predictions from all the weak learners are combined, and the final output is the class that gets the most votes among all weak learners.")
在sklearn当中,有两个Bagging集成算法,分别是随机森林(RandomForest)和极端随机树(ExtraTrees),这两种算法都是以决策树为弱评估器的有监督算法,用于分类、回归、排序等各种任务。
另外,还可以使用bagging的思路对其它算法进行集成,比如使用装袋法分类的类BaggingClassifier对支持向量机或逻辑回归进行集成。对应如下:
- 随机森林分类:RandmForestClassifier
- 随机森林回归:RandomForestRegressor
- 极端随机树分类:ExtraTreesClassifier
- 极端随机树回归:ExtraTreesRegressor
- 装袋法分类:BaggingClassifier
- 装袋法回归BaggingRegressor
五、随机森林原理
随机森林是一种集成学习方法,它的构建过程主要分为三个步骤:
- 自助抽样(Bootstrap Sampling):有放回的抽样生成多个子数据集
- 构建决策树:对每个子数据集构建一个决策树
- 预测:如果是回归问题,随机森林的预测是所有决策树预测的平均值,如果是分类问题,每个决策树都会进行投票,随机森林的预测是获得最多票数的类别。
简单来说随机森林算法的构建过程可以这样来描述:从提供的数据中随机抽样出不同的子集,用于建立多棵不同的决策树,并按照Bagging的规则对单棵决策树的结果进行集成(回归则平均,分类则少数服从多数)。所以只要掌握了决策树的各项属性和参数,随机森林的大部分内容都相当容易理解。
上述三个过程是不难理解的,但是每个过程会有一些使用上的小细节,下面就通过一个实际的案例,来搞清楚随机森林到底有哪些需要注意的参数和细节。
六、随机森林在Sklearn中的建模示例
6.1 参数总览
在sklearn中,随机森林可以应用于分类和回归两大任务,具体来说有RandomForestClassifier和RandomForestRegressor两个主要的类。
其实可以很明显的看出来,随机森林回归器和分类器的参数高度一致,在使用方式上也可以像调用逻辑回归、决策树等其他sklearn中的算法一样,要依次进行实例化、fit、predict/score来完成相关的任务。
回归森林的默认评估指标为R2,分类森林的默认评估指标为准确率。
6.2 使用随机森林回归建模示例
随机森林有大量的参数,在Sklearn中实现的随机森林所有参数都有默认值,因此即便不学习任何参数,也可以调用随机森林算法完成建模。过程如下:
- Step 1: 导入必要的库
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.tree import DecisionTreeRegressor as DTR
# cross_val_score与cross_validate的区别就是:cross_validate能够输出训练集分数
from sklearn.model_selection import cross_validate, KFold
- Step2:读取数据集并查看
数据集来自Kaggle中House Price竞赛,地址:https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/overview
本文使用的数据集已完成初步的预处理工作
data = pd.read_csv("../../../../datasets/HousePrice/train_encode.csv", index_col=0)
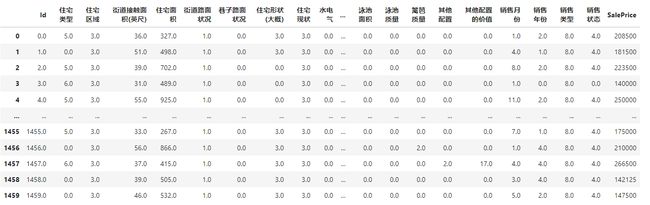
数据情况如下:
- Step 3:初步的数据探索
读取到数据后,初步查看一下数据的情况,了解数据,代码如下:
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
# # 数据的基本信息
# print("Basic Information:")
# print(data.info())
# 1. 数据的大小
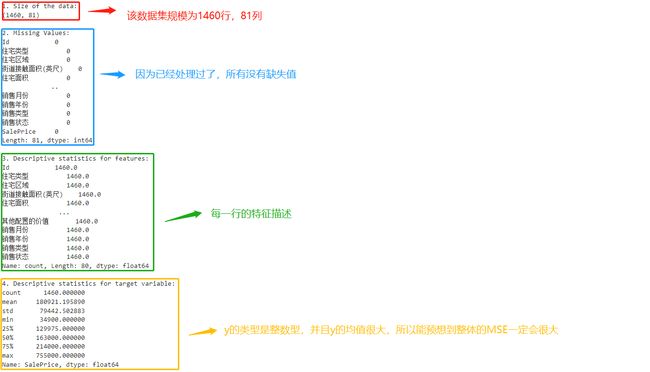
print("1. Size of the data:")
print(data.shape)
# 2. 缺失值
print("\n2. Missing Values:")
print(data.isnull().sum())
# 3. x的数据描述
print("\n3. Descriptive statistics for features:")
print(X.describe().iloc[0]) # 打印第一行,即count
# 4. y的取值描述
print("\n4. Descriptive statistics for target variable:")
print(y.describe())
看下数据情况:
- Step 4:使用RandomForestRegressor默认参数配合交叉验证建模
import time
def random_forest_cross_validation(X, y, n_estimators=100, cv=None):
"""
使用随机森林回归器并应用交叉验证。
参数:
- X: 特征数据
- y: 目标变量
- n_estimators: 随机森林中的树的数量
- cv: 交叉验证方法实例
返回:
- scores: 交叉验证的结果
"""
# 创建随机森林回归器实例
rf_regressor = RandomForestRegressor(n_estimators=n_estimators, random_state=42)
# 记录开始时间
start_time = time.time()
# 使用交叉验证评估模型
scores = cross_validate(rf_regressor, # 评估器
X, # 特征
y, # 标签
cv=cv, # 交叉验证参数
scoring=('neg_mean_squared_error'), # 评估指标
return_train_score=True # 返回训练分数
)
# 记录结束时间,并计算训练时长
end_time = time.time()
elapsed_time = end_time - start_time
# 打印训练时间
print(f"总训练时间: {elapsed_time:.2f} 秒")
return scores
- Step 5:运行函数并做结果解析
# 定义交叉验证方式
cv = KFold(n_splits=5, shuffle=True, random_state=1412)
# 使用函数
scores = random_forest_cross_validation(X, y, cv=cv)
# 打印交叉验证结果
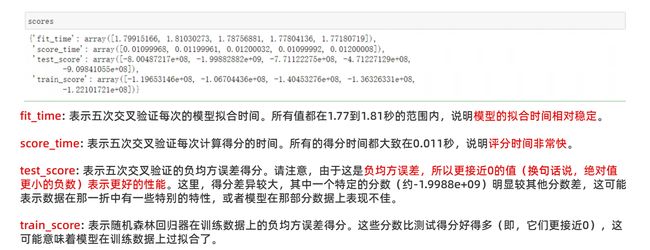
print("交叉验证均方误差得分:", scores['test_score'])
print("平均均方误差得分:", scores['test_score'].mean())
输出如下:
如果进一步解析模型返回的scores,其形式是这样的:
所以针对上述的训练结果综合分析:训练得分明显优于测试得分,这意味着模型在训练数据上存在过拟合。
- Step 6:尝试使用决策树建模
from sklearn.tree import DecisionTreeRegressor
def decision_tree_cross_validation(X, y, cv=None):
"""
使用决策树回归器并应用交叉验证。
参数:
- X: 特征数据
- y: 目标变量
- cv: 交叉验证方法实例
返回:
- scores: 交叉验证的结果
"""
# 创建决策树回归器实例
dt_regressor = DecisionTreeRegressor(random_state=42)
# 记录开始时间
start_time = time.time()
# 使用交叉验证评估模型
scores = cross_validate(dt_regressor, # 评估器
X, # 特征
y, # 标签
cv=cv, # 交叉验证参数
scoring=('neg_mean_squared_error'), # 评估指标
return_train_score=True # 返回训练分数
)
# 记录结束时间,并计算训练时长
end_time = time.time()
elapsed_time = end_time - start_time
# 打印训练时间
print(f"总训练时间: {elapsed_time:.2f} 秒")
return scores
# 使用函数
scores_dt = decision_tree_cross_validation(X, y, cv=cv)
# 打印交叉验证结果
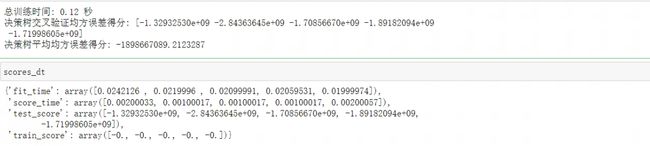
print("决策树交叉验证均方误差得分:", scores_dt['test_score'])
print("决策树平均均方误差得分:", scores_dt['test_score'].mean())
看下结果:
从结果上来分析:训练误差都是0,这意味着决策树在训练集上做到了完美拟合,而测试误差在1.33e+09至2.84e+09之间变化,这说明了这次的建模是超级过拟合状态。
- Step 7:对比分析
对于同一个数据集,决策树和随机森林都在默认参数下得到的结果也是不尽相同的,主要问题如下:
-
决策树在测试集上的均方误差相较于随机森林模型有所增加(训练集和测试在交叉验证上的分数差异更大),因此森林的过拟合程度没有决策树高,这说明随机森林模型在这个任务上可能更为适合。
-
与随机森林相比,决策树的训练时间显著缩短。这是因为决策树只有一个模型需要训练,而随机森林则需要训练多个决策树。
- Step 8:计算随机森林和决策树的RMSE
在集成学习中,衡量回归类算法的指标一般是RMSE(根均方误差),也就是MSE开根号后的结果。现实数据的标签往往数字巨大、数据量庞杂,MSE作为平方结果会放大现实数据上的误差(例如随机森林结果中得到的, 7 ∗ 1 0 8 7*10^8 7∗108等结果)。如果使用RMSE的话,计算代码如下:
# 计算随机森林的RMSE
rf_train_rmse = np.sqrt(abs(scores["train_score"]))
rf_test_rmse = np.sqrt(abs(scores["test_score"]))
# 计算决策树的RMSE
dt_train_rmse = np.sqrt(abs(scores_dt["train_score"]))
dt_test_rmse = np.sqrt(abs(scores_dt["test_score"]))
print(f"随机森林训练数据的平均RMSE: {rf_train_rmse.mean():.2f}")
print(f"随机森林测试数据的平均RMSE: {rf_test_rmse.mean():.2f}")
print(f"决策树训练数据的平均RMSE: {dt_train_rmse.mean():.2f}")
print(f"决策树测试数据的平均RMSE: {dt_test_rmse.mean():.2f}")
- Step 9:绘制图像
# 准备数据
models = [
{"rmse_train": rf_train_rmse, "rmse_test": rf_test_rmse, "color": "green", "label": "RandomForest"},
{"rmse_train": dt_train_rmse, "rmse_test": dt_test_rmse, "color": "orange", "label": "DecisionTree"}
]
xaxis = range(1,6)
plt.figure(figsize=(8,6), dpi=80)
# 使用循环绘制线条
for model in models:
plt.plot(xaxis, model["rmse_train"], color=model["color"], label=f"{model['label']}Train")
plt.plot(xaxis, model["rmse_test"], color=model["color"], linestyle="--", label=f"{model['label']}Test")
# 设置轴标题、图例和轴标签
plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts", fontsize=16)
plt.ylabel("RMSE", fontsize=16)
plt.legend()
plt.show()
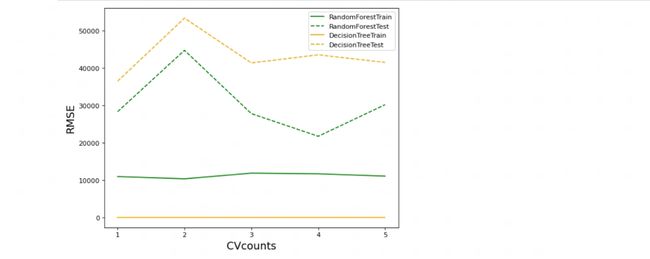
图像如下:
横坐标:交叉验证次数,纵坐标:RMSE数值
从图像中可见,虽然随机森林和决策树都显示出过拟合的迹象,但随机森林的过拟合程度明显较小。在训练集上,决策树达到了完美的拟合,其RMSE为0,而随机森林的训练集上的RMSE约在1万左右。然而,对于测试集,随机森林的表现明显优于决策树。这验证了一个观点:与特定的参数配置相比,随机森林本质上比决策树具有更强的泛化能力和更低的过拟合风险。
尽管随机森林效果优于决策树,但也存在着过拟合问题,这通常意味着模型可能捕获了训练数据中的一些噪音,而不只是基本的模式。所以需要考虑调整随机森林的一些参数(例如,减少树的深度、增加样本叶子的最小数量等)来减少过拟合。
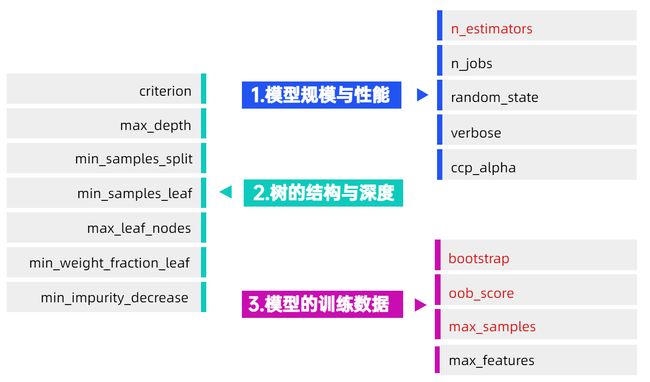
七、随机森林在Sklearn中的参数详解
随机森林回归器的参数数量还是比较多,为了便于理解,可以根据其用处和功能进行参数分类,如下:
根据这种分类规则,在进行参数调优的时候,可以先决定模型的规模和性能,然后调整树的结构和深度,接着优化样本和特征选择,最后考虑其他参数。
7.1 模型规模与性能
- 参数1:n_estimators
n_estimators参数在随机森林中表示弱评估器(通常是决策树)的数量,在sklearn中默认100,它是唯一一个必填的参数。
对单一决策树而言,模型复杂度由树结构(树深、树宽、树上的叶子数量等)与数据量(样本量、特征量)决定,而对随机森林而言,模型复杂度由森林中树的数量、树结构与数据量决定,树的数量越多,模型越复杂。因此在调整n_estimators时,要在模型效果与训练难度之间取得平衡,同时还需要使用交叉验证来随时关注模型过拟合的情况。
7.2 树的结构与深度
随机森林的预测精度和稳定性主要受其组成的弱评估器(通常是决策树)的影响。每一棵树的结构、深度和多样性都会对随机森林的效率、泛化能力及其是否过拟合产生直接效果。单棵树的复杂度越高,随机森林的整体计算复杂度也会上升,增加计算时间并有过拟合的风险。因此,适当地调节和优化每一棵树是确保随机森林效果良好的关键。简而言之,调控每个弱评估器的结构至关重要,因为其复杂性和预测表现都会在全局上影响随机森林的结果。
随机森林的这些参数与决策树类DecisionTreeRegressor中完全一致,用于对决策树进行剪枝、控制单个弱评估器的结构。其中需要重点关注的几个参数如下:
- 参数1:criterion
在随机森林中,criterion 参数用于确定如何对特征进行分割以构建树结构。它指定了衡量分割质量的方法。criterion 参数对于随机森林分类器和回归器都是存在的,但所使用的标准略有不同。在随机森林分类树 (RandomForestClassifier)中,衡量指标就是基尼系数或者信息熵,在之前的文章已经讲过了,此处不再重复说,不太清楚的看这篇文章:
机器学习(十六):决策树
重点说一下随机森林回归器树 (RandomForestRegressor),回归树中的criterion可以选择**“squared_error”(平方误差),“absolute_error”(绝对误差)以及"poisson"(泊松偏差)**。对任意样本 i i i而言, y i y_i yi为真实标签, y i ^ \hat{y_i} yi^为预测标签,则各个criterion的表达式为:
- 平方误差 (MSE, Mean Squared Error)
MSE 是最常用的回归损失函数之一,它试图最小化实际值和预测值之间的平方差。这也意味着大的误差会受到更大的惩罚,因为误差的平方会增大差距。
M S E = ∑ ( y i − y i ^ ) 2 (1) MSE = \sum{(y_i - \hat{y_i})^2} \tag{1} MSE=∑(yi−yi^)2(1)
- 绝对误差 (MAE, Mean Absolute Error)
MAE 对所有误差施加相同的权重,无论它们的大小。这使得模型更对异常值更为稳健,因为它不会像 MSE 那样对大的误差给予额外的惩罚。
M A E = ∑ ∣ y i − y i ^ ∣ (2) MAE = \sum{|y_i - \hat{y_i}|} \tag{2} MAE=∑∣yi−yi^∣(2)
- 泊松偏差 (Poisson Deviance)
泊松偏差常用于计数数据和模型泊松分布的数据。当目标变量代表计数或频率时,这是一个很好的选择。它衡量观察到的计数和预测的计数之间的差异。
P o i s s o n = 2 ∑ ( y i l o g ( y i y i ^ ) − ( y i − y i ^ ) ) (3) Poisson = 2\sum{(y_ilog(\frac{y_i}{\hat{y_i}})-(y_i - \hat{y_i}))} \tag{3} Poisson=2∑(yilog(yi^yi)−(yi−yi^))(3)
总的来说:作为分枝标准,平方误差比绝对误差更敏感(类似于信息熵比基尼系数更敏感),并且在计算上平方误差比绝对误差快很多。泊松偏差则是适用于一个特殊场景的:当需要预测的标签全部为正整数时,标签的分布可以被认为是类似于泊松分布的。
场景:城市公交车站的乘客到达率
假设你是一个城市的交通规划师,你想预测特定公交车站在特定时间段(例如,每小时)的乘客到达数量。这是一个典型的计数问题,因为你正在预测一个非负整数(即到达的乘客数量)。
你有过去几个月的数据,显示了每小时到达每个站点的乘客数量。你注意到到达数量有一些固定的模式(例如,早晨和下午高峰期的到达率高于其他时间),但也有一些随机性。
在这种情况下,到达的乘客数量可能会遵循一个泊松分布,这是描述给定时间段内发生的独立事件数量的典型分布。
为了预测未来的乘客到达数量,就可以使用随机森林回归模型并选择泊松偏差作为损失函数。这样,模型会考虑到数据的泊松特性,可能会比其他损失函数提供更准确的预测。
这只是使用泊松偏差的一个例子,实际上,任何你希望预测计数的问题,特别是当这些计数有一定的随机性时,泊松偏差都可能是一个合适的选择。
正整数预测在实际应用中非常常见,比如预测点击量、预测客户/离职人数、预测销售量等。
其实在实际应用中,选择criterion的唯一指标就是最终的交叉验证结果——无论理论是如何说明的,只取令随机森林的预测结果最好的criterion。
- 参数2:max_depth
这个参数用于控制树的深度,默认值为None。从树结构层面来看,它是对随机森林抗过拟合能力影响最大的参数,因此当随机森林表现为过拟合时,选择一个小的max_depth会很有效。
- 参数3:max_leaf_nodes与min_sample_split
比max_depth更精细的减枝方式,但限制叶子数量和分枝,既可以实现微调,也可以实现大刀阔斧的剪枝。max_leaf_nodes的默认值为None,即不限叶子数量。min_sample_split的默认值为2,等同于不限制分枝。
- 参数4:min_impurity_decrease
最精细的减枝方式,可以根据不纯度下降的程度减掉相应的叶子。默认值为0,因此是个相当有空间的参数。
7.3 模型的训练数据
决策树在分枝的时候会找到每个特征不纯度下降程度最大的节点进行分枝,因此原则上来说,只要给出数据一致、并且不对决策树进行减枝的话,决策树的结构一定是完全相同的。对集成算法来说,平均多棵相同的决策树的结果并没有意义,因此集成算法中每棵树必然是不同的树,所以随机森林采用Bagging算法,依赖于随机抽样数据来实现这一点的。
随机森林会从提供的数据中随机抽样出不同的子集,用于建立多棵不同的决策树,最终再按照Bagging的规则对众多决策树的结果进行集成。相关的参数如下:
- 参数1:bootstrap
bootstrap 参数用来控制是否使用自助采样来创建每棵树的训练数据。输入为布尔值。
-
如果 bootstrap=True(默认值),则对于训练每棵树,都会使用自助采样方法从原始数据中抽取样本。
-
如果 bootstrap=False,则每棵树都会使用完整的原始数据集进行训练。
在随机森林中它特指有放回随机抽样技术,具体过程如下:
假设存在一个含有m个样本的原始训练集,要对它进行随机采样。每次采样一个样本,并在抽取下一个样本之前将该样本放回原始训练集,也就是说下次采样时这个样本依然可能被采集到,这样采集max_samples次,最终得到max_samples个样本组成的自助集。
通常来说,max_samples是等于m的(行业惯例),也就是抽样数据集的大小与原始数据集一致,但是如果原始数据集太大、或者太小,也可以自由调整max_samples的大小。由于是随机采样,这样每次的自助集和原始数据集不同,和其他的采样集也是不同的。这样就可以自由创造取之不尽用之不竭,并且互不相同的自助集,用这些自助集来训练弱分类器,弱分类器自然也就各不相同了。
然而有放回抽样也会有自己的问题。由于是有放回,一些样本可能在同一个自助集中出现多次,而其他一些却可能被忽略。当抽样次数足够多、且原始数据集足够大时,自助集大约平均会包含全数据的63%,这个数字是有数学依据的。因为在max_samples次抽样中,一个样本被抽到某个自助集中的概率为:
1 − ( 1 − 1 m ) m a x _ s a m p l e s (4) 1-(1-\frac{1}{m})^{max\_samples} \tag{4} 1−(1−m1)max_samples(4)
对于任意一个样本而言,一次抽样时抽到该样本的概率为:
1 m (5) \frac{1}{m} \tag{5} m1(5)
一次抽样时抽不到该样本的概率为:
1 − 1 m (6) 1-\frac{1}{m} \tag{6} 1−m1(6)
总共抽样max_samples次,一次也没有抽到该样本的概率就是
( 1 − 1 m ) m a x _ s a m p l e s (7) (1-\frac{1}{m})^{max\_samples} \tag{7} (1−m1)max_samples(7)
因此1减去该概率,就是一个样本在抽样中一定会被抽到某个自助集的概率,当m刚好等于max_samples时,公式可以被修改为:
1 − ( 1 − 1 m ) m (8) 1-(1-\frac{1}{m})^{m} \tag{8} 1−(1−m1)m(8)
这是一个经典的极限问题,由洛必达法则(L’Hôpital’s rule)可知:当m足够大时(接近极限时),这个概率收敛于1-(1/e),其中e是自然常数,整体概率约等于0.632。因此,会有约37%的训练数据被浪费掉,没有参与建模,这些数据被称为袋外数据(out of bag data,简写为oob)。在实际使用随机森林时,袋外数据常常被当做验证集使用。
- 参数2:oob_score
使用oob_score参数的前提是:boostrap=True
oob_score控制是否使用袋外数据进行验证,输入为布尔值,默认为False,如果希望使用袋外数据进行验证,修改为True即可。
- 参数3:max_samples
max_samples表示自助集的大小,可以输入整数、浮点数或None,默认为None。
如果使用袋外数据时,可以用随机森林的另一个重要属性:oob_score_来查看在袋外数据上测试的结果,oob_score_输出的评估指标默认是R2,并且不支持修改。
- 参数4:max_features
在随机森林中max_features的用法与决策树中完全一致,具体如下:
- 输入整数,表示每次分枝时随机抽取max_features个特征
- 输入浮点数,表示每次分枝时抽取round(max_features * n_features)个特征
- 输入"auto"或者None,表示每次分枝时使用全部特征n_features
- 输入"sqrt",表示每次分枝时使用sqrt(n_features)
- 输入"log2",表示每次分枝时使用log2(n_features)
无论对数据进行怎样的抽样,能够控制的都只是建立单棵树时的数据而已。在总数据量有限的情况下,单棵树使用的数据量越大,每一棵树使用的数据就会越相似,每棵树的结构也就会越相似,bagging的效果难以发挥、模型也很容易变得过拟合。因此,当数据量足够时,往往会消减单棵树使用的数据量。
具体如下:
- 输入整数,表示每次分枝时随机抽取max_features个特征
- 输入浮点数,表示每次分枝时抽取round(max_features * n_features)个特征
- 输入"auto"或者None,表示每次分枝时使用全部特征n_features
- 输入"sqrt",表示每次分枝时使用sqrt(n_features)
- 输入"log2",表示每次分枝时使用log2(n_features)
无论对数据进行怎样的抽样,能够控制的都只是建立单棵树时的数据而已。在总数据量有限的情况下,单棵树使用的数据量越大,每一棵树使用的数据就会越相似,每棵树的结构也就会越相似,bagging的效果难以发挥、模型也很容易变得过拟合。因此,当数据量足够时,往往会消减单棵树使用的数据量。
八、总结
本文深入探讨了集成学习及其在随机森林中的应用。对集成学习的基本概念、优势以及为何它有效做了阐述。随机森林,作为一个集成学习方法,与Bagging有紧密联系,其核心思想和实现过程均在文中进行了说明。还详细展示了如何在Sklearn中利用随机森林进行建模,并对其关键参数进行了解读,希望能帮助大家更有效地运用随机森林进行数据建模。
最后,感谢您阅读这篇文章!如果您觉得有所收获,别忘了点赞、收藏并关注我,这是我持续创作的动力。您有任何问题或建议,都可以在评论区留言,我会尽力回答并接受您的反馈。如果您希望了解某个特定主题,也欢迎告诉我,我会乐于创作与之相关的文章。谢谢您的支持,期待与您共同成长!
参考:[Breiman, L. (1996). Bagging predictors. Machine Learning, 24(2), 123-140](Bagging Predictors (springer.com))