长度最小的子数组(滑动窗口)
题目1:给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
解题思路:
1、暴力解法,通过两层for循环直接完成,但是时间复杂度为O(n²)。
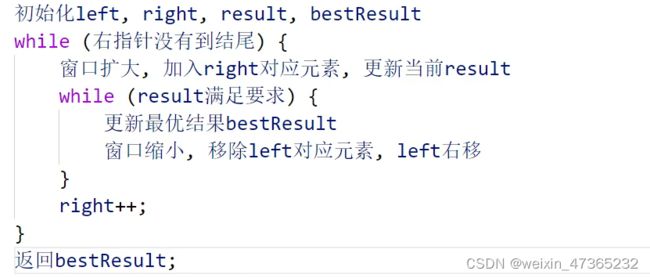
2、窗口滑动。
通过双指针进行遍历,两个指针中间区域看作一个窗口,首先right指针向右移动,当窗口里面的值大于target,也就是满足题目条件时,left指针开始移动,直到结束内层循环。
关键点:
1、内层需要通过while语句进行循环判断,而不能通过if语句判断。
2、对于result的初始值,设为Integer.MAX_VALUE
时间复杂度理解:虽然本题解法也采用两层的循环,但是时间复杂度为(n)。本题最复杂的状态就是right滑动了n次,left滑动了n-1次,总共滑动了2n-1次。
答案代码:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0;
int right = 0;
//由于要找最小长度,因此结果变量定义赋值为最大
int result = Integer.MAX_VALUE;
int sum = 0;
while(right < nums.length)
{
sum += nums[right];
//注意这一步,滑动窗口左边可能会滑动多次,因此内层不能使用if判断
while( sum >= target)
{
int min = right - left + 1;
result = result < min ? result : min;
sum -= nums[left];
left ++;
}
right++;
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}
总结:通过整理网上的资料,得出滑动窗口一般使用的场景。
关键字暗示:子串/子数组/子序列;最长/最短;无重复/覆盖/串联(一种限制性词语)。
题目2:你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
示例 1:
输入:fruits = [1,2,1]
输出:3
解释:可以采摘全部 3 棵树。
示例 2:
输入:fruits = [0,1,2,2]
输出:3
解释:可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘,则只能采摘 [0,1] 这两棵树。
解题思路:
通过本题,对于窗口滑动加深了理解。窗口滑动有一个很关键的地方,就是对于内层循环条件的设计,很多题目的限制条件(无重复,串联等)指的就是这个条件。
本题中,通过Map集合不重复的特性和size()方法,可以很好的解决给出的限制条件,因此把问题转移到对Map集合的维护上。而Map集合维护最关键的点在于对于remove键值的确定。以下是具体remove()键值的确定思路:
当right位置出现新类型导致size()值大于3,最好的方法就是从right位置逆序找到第二种和right位置不同的值,而这个位置就是left下一个初始值的左边。因此令left = right - 2,当fruits[right - 1] != fruits[left]时跳出循环,此时fruits[left]就是要被remove的键值。
本题还有两个细节:
1、由于本题有 left–,left = right - 2这种形式的语句,因此要十分注意对于数组边界的判断,防止数组溢出。在本题中,由于语句执行的前提是size()>2,也就是至少数组有三个不同的元素,数组的length肯定是大于等于3的,因此left = right - 2不会溢出。由于 left–跳出循环的条件肯定是可以在数组大小允许范围内得出,因此也不会溢出。
2、这是最容易忽视的一点,由于外层循环的跳出条件是right等于数组的长度,此时size()<=2,因此最后一种收集水果的方案是可行的,需要计算在内,并且于max比较,最后返回两者中的最大值。
答案代码:
class Solution {
public int totalFruit(int[] fruits) {
int max = 0;
int left = 0;
int right = 0;
HashMap<Integer, Integer> map = new HashMap<>();
while (right < fruits.length) {
//注意因为后面又remove会删除,因此这里每次都加入即可
map.put(fruits[right],right);
if(map.size() > 2) //种类超过两种
{ //计算当前的最大数目,并且和之前的max进行比较
max = Math.max(max,right - left);
//这里其实是通过right左移找到键值,但是为了便于维护变量,直接通过left左移,也更容易定位left
left = right - 2;
//找出需要删除的键值
while (fruits[right - 1] == fruits[left] )
{
left--;
}
//移除键值
map.remove(fruits[left]);
//left确定新起点
left++;
}
right++;
}
//注意最后返回一定要进行判断
//因为right跳出外层循环时,map.size()没有大于2
//因此最后一种收集水果的数目没有计算
return max > right - left ? max : right - left;
}
}