有向图的强连通分量（SCC）

有向图的强连通分量（SCC）

1. 有向图的强连通分量原理

原理

• 强连通分量是针对有向图来说的。如下的讲解默认都是针对有向图的。

• 连通分量：对于一个有向图中的一些点来说，如果任意两点都能相互到达，则称这些点以及对应的边构成连通分量。

• 强连通分量：指极大连通分量。即该联通分量中增加任何一个点都不能构成连通分量了。

• 那么强连通分量有什么作用呢？

  我们可以通过使用求解强联通分量的方式将一个有向图缩点成有向无环图（DAG），也称为拓扑图。缩点：指将强联通分量缩成一个点。

  

  转化为拓扑图有什么好处呢？其中一个好处是我们在求解最短路/最长路的时候可以使用递推的方式求解。

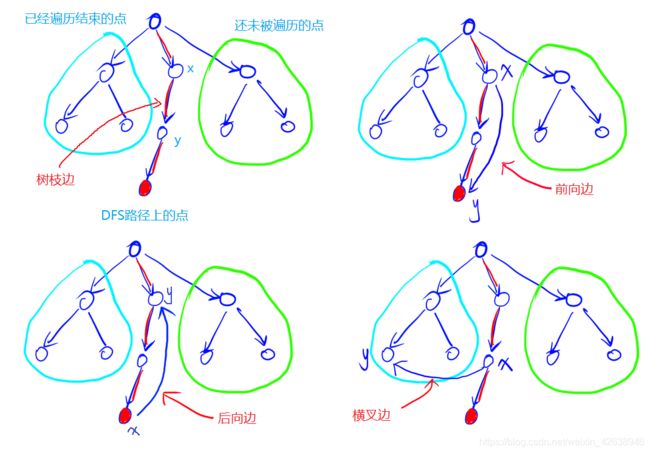
• 下面就要考虑如何求解强联通分量了，我们采用DFS的方式求解。下面首先介绍一下在DFS过程中的各种边的分类：

（1）树枝边（x, y）：x是y的父节点；

（2）前向边（x, y）：x是y的祖先节点，因此树枝边是一种特殊的前向边；

（3）后向边（x, y）：y是x的祖先节点，并且从x还能回到y，这样回去的边（x, y）称为后向边；

（4）横叉边（x, y）：从当前DFS路径上的点x连向已经搜索完毕的的点y的边。

• 我们只需要熟悉一下这几个名词即可。
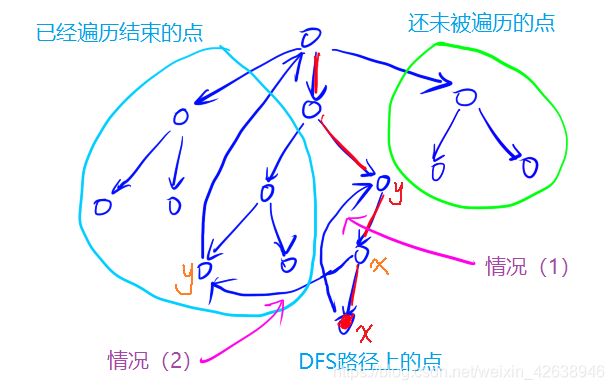
• 如何判断某个点x是否在一个强联通分量中呢？存在以下两种情况：

（1）存在后向边指向祖先节点；

（2）从当前点x可以经过横插边边走到点y，点y可以走到x的祖先节点。

---

• 基于上面的原理，我们直接给出求SCC的算法，即tarjan算法。

• 这里引入时间戳（从1开始计数）的概念，根据DFS过程中每个节点遍历到的顺序依次给每个节点递增赋值。对于树枝边和前向边（x, y），y的时间戳大于x的时间戳；对于后向边和横叉边（x, y），y的时间戳小于x的时间戳。

• 对于每个节点，定义两个时间戳：$dfn[u]$和$low[u]$。

  $dfn[u]$：表示遍历到u的时间戳；

  low[u]：从u开始走，所能遍历到的最小时间戳。

• 我们每次求解的是每个强连通分量所在的最高点。如果u是其所在的强联通分量的最高点$⟺dfn[u]==low[u]$。

• 该做法的证明这里略过，这个证明一般使用不到。

• 因为每个点我们只会遍历一次，时间复杂度一般是$O(n+m)$的。

• 求完强联通分量之后就可以缩点了，设$id[u]$表示点u所在的强连通分量的编号（求SCC的时候可以求出来），则缩点过程如下：

for (int i = 1; i <= n; i++)
	for (i的所有临点j)
		if (id[i] != id[j])
			加一条id[i]到id[j]的新边

• 做完tarjan算法之后，强联通分量按照编号递减的顺序就已经是拓扑序了，因此后面就不需要再做一遍拓扑排序了（这是因为求拓扑序存在两种做法，一种是我们最熟悉的宽搜；另一种是深搜，将深搜过程中遍历到的点记录到seq中，则seq的逆序就是拓扑序）

2. AcWing上的有向图的SCC题目

AcWing 1174. 受欢迎的牛

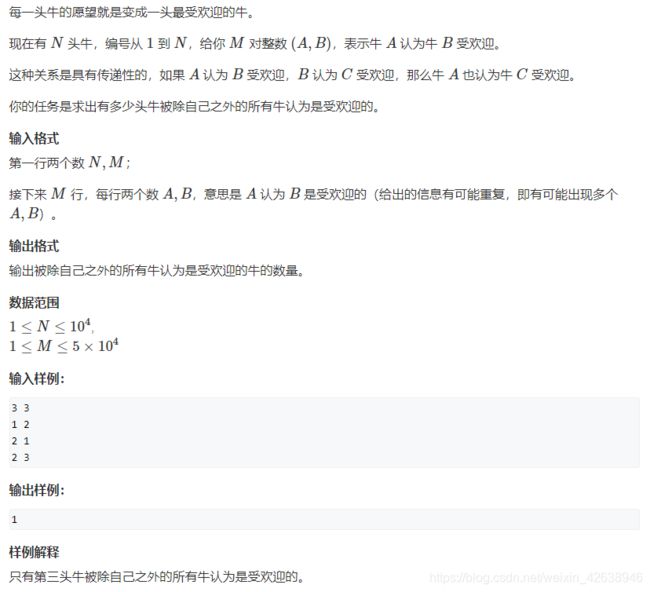
问题描述

• 问题链接：AcWing 1174. 受欢迎的牛

  

分析

• 如果A认为B受欢迎，则从A向B连接一条有向边。
• 这一题可以使用floyd算法求闭包，然后统计每个点的入度是不是n-1，如果是的话说明该头牛被所有其他的牛所欢迎。但是这种做法会超时。
• 考虑一下，如果这个图是DAG的话，如果存在大于等于两个点的出度为0，则说明没有一头牛符合要求；如果只有一个点的出度为0，则说明这头牛被所有其他的牛所欢迎。
• 因此我们可以考虑对这个图求强联通分量，然后缩点（即将每个SCC看成一个点）建图，然后看新图是不是只有一个点的出度为0，如果是的话，新图中该点对应原图中的SCC中点的数量就是答案。
• 其实我们没有必要真正将新图建立出来，我们只需要统计一下每个SCC的出度即可。

代码

• C++

#include 
#include 

using namespace std;

const int N = 10010, M = 50010;

int n, m;  // 点数、边数
int h[N], e[M], ne[M], idx;

int dfn[N];  // dfn[u]: 表示遍历到u的时间戳
int low[N];  // low[n]: 从u开始走，所能遍历到的最小时间戳。
int timestamp;  // 时间戳

int stk[N], top;  // 存储在当前SCC中的点
bool in_stk[N];  // 表示某个点是否在栈中

int id[N];  // 表示某个点所在的SCC编号
int scc_cnt;  // 表示当前有多少个SCC
int sz[N];  // 表示每个SCC中点的数量

int dout[N];  // 表示每个SCC的出度是多少

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {
    
    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u, in_stk[u] = true;  // 将当前点加入栈中
    
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {  // 如果点j没有被遍历过，则遍历j
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u]) {  // 说明u是当前SCC的最高点
        ++scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            sz[scc_cnt]++;
        } while (y != u);
    }
}

int main() {
    
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    
    // tarjan算法
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
    
    // 建图，这里只需要求出每个SCC的出度
    for (int i = 1; i <= n; i++)    
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];  // 边(i, k)
            int a = id[i], b = id[k];  // i,k所在的SCC的编号
            if (a != b) dout[a]++;
        }

    int zeros = 0;  // 出队为0的SCC的数量
    int sum = 0;  // 出度为0的SCC中点的数量
    for (int i = 1; i <= scc_cnt; i++)
        if (!dout[i]) {
            zeros++;
            sum += sz[i];
            if (zeros > 1) {  // 多于一个SCC出队为0，没有满足条件的点
                sum = 0;
                break;
            }
        }
    
    printf("%d\n", sum);
    
    return 0;
}

AcWing 367. 学校网络

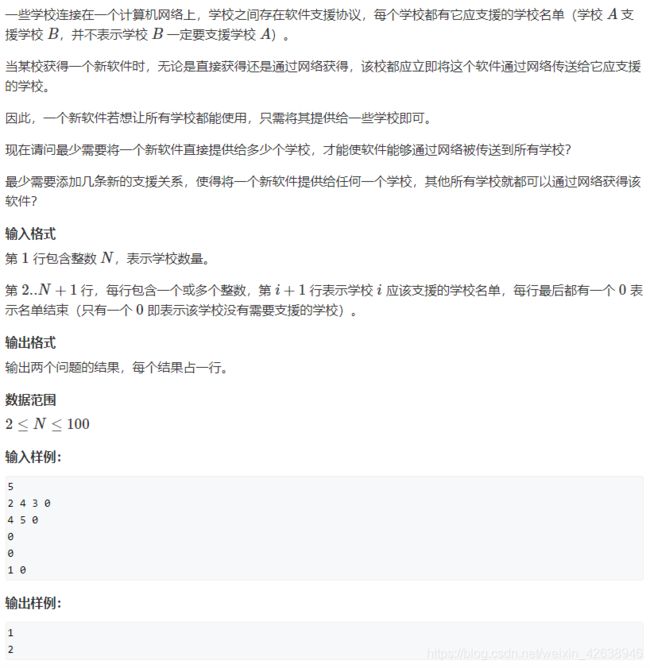
问题描述

• 问题链接：AcWing 367. 学校网络

  

分析

• 本题相当于给了我们一张有向图，一旦一个点得到一个软件，这个点就可以将这个软件传给它指向的边，以此类推，然后问我们两个问题：

（1）我们至少需要将一个软件给多少个点，然后所有的点都可以得到这个软件？

（2）如果我们将一个软件给任意一个点，则其他点都能得到这个软件，需要至少条件多少边？（至少加几条边，可以将整个图变为一个SCC）

• 我们可以考虑缩点之后的新图，假设新图中有P个起点（即入度为0的点），Q个终点（即出度为0的点）。则第（1）问的答案是P，这是因为我们至少发P个，发P个之后每个点都能得到这个软件；第（2）问的答案是MAX(P, Q)，另外如果原图本来就是一个SCC，则答案是0，需要特判一下。

• 关于第（2）问答案的证明，因为起点和终点是对称的，不妨设$|P|\le |Q|$，证明一下答案是$|Q|$。

  ① 如果$|P|==1$，我们只需要让所有终点向起点连一条边，即新增$|Q|$条边，即可让整个图变为一个SCC；

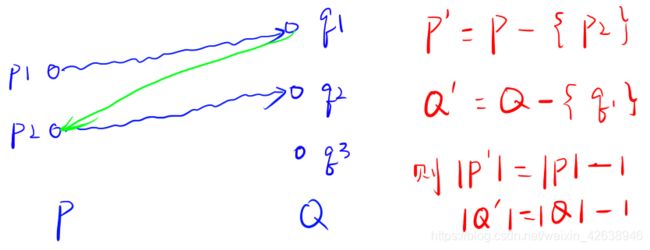
  ② 如果$|P|>1$，则$|Q|\ge |P|>1$，则至少存在两个起点，而且这两个起点到达两个不同的终点（可以用反证法证明这一点，假设如果找不到这样的两个起点，则所有的起点必定都到达一个终点，和$|Q|\ge 2$矛盾），我们可以像下图那样添加边：

  

  只要我们添加一条边，起点终点数量都为减少一个。因为当我们添加$|P|-1$条边后，只有一个起点了，此时还有$|Q|-(|P|-1)$个终点，根据①，此时还需要增加$|Q|-(|P|-1)$即可让整个图变为一个SCC；因此需要增加的边数为：$|P|-1+|Q|-(|P|-1)=|Q|$条边。证明完毕。

代码

• C++

#include 
#include 

using namespace std;

const int N = 110, M = 10010;

int n;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt;
int din[N], dout[N];  // 每个SCC的入度、出度

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {
    
    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u, in_stk[u] = true;
    
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u]) {
        ++ scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
        } while (y != u);
    }
}

int main() {
    
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++) {
        int t;
        while (cin >> t, t) add(i, t);
    }
    
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
    
    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];  // (i, k)
            int a = id[i], b = id[k];
            if (a != b) {
                dout[a]++;
                din[b]++;
            }
        }
    
    int P = 0, Q = 0;
    for (int i = 1; i <= scc_cnt; i++) {
        if (!din[i]) P++;
        if (!dout[i]) Q++;
    }
    
    printf("%d\n", P);
    if (scc_cnt == 1) puts("0");
    else printf("%d\n", max(P, Q));
    
    return 0;
}

AcWing 1175. 最大半连通子图

问题描述

• 问题链接：AcWing 1175. 最大半连通子图

  

分析

• 半连通子图只需要满足图中的点单向可到达即可（当然双向可到达也是可以的），根据定义可知强联通分量一定是半连通子图。
• 另外如果固定了点，则导出子图一定也是固定的，与之相关的边必须全部选上，即使是重边也必须全部选上。
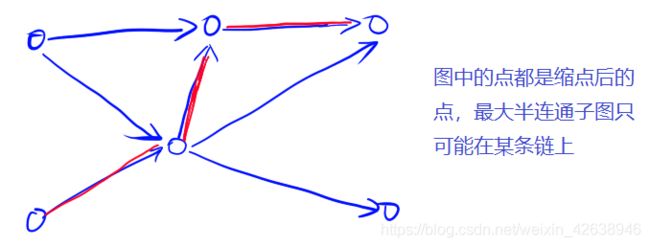
• 因此我们的做法是：①首先求解强联通分量，②然后缩点，建图（注意重边需要判重）③最后在DAG上找到一个最长链（所谓最长是指链上的点最多），这条链上的点的数目就是最大半连通子图的点的数目

• 因为是拓扑图，所以可以采用递推的方式求解最大半连通子图中点的数目以及对应的方案数，本质上是一个DP。
• 定义$f[i]$和$g[i]$。

（1）$f[i]$：表示以第 i 个点为终点的最长链节点数量之和；

（2）$g[i]$：让$f[i]$取到最大值对应的方案数；

• 如果存在一条从i到k的边，则状态转移如下：

（1）如果$f[k]<f[i]+scc\_size[k]$，则$f[k]=f[i]+scc\_size[k],g[k]=g[i]$；

（2）如果$f[k]==f[i]+scc\_size[k]$，则$g[k]+=g[i]$；

• 另外对于重边我们只需要判断一次即可，需要去重，使用哈希表即可，如果边是$(a,b)$，则哈希函数设为$a\times 1000000ll+b$。

代码

• C++

#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, M = 2000010;  // 因为要建新图，两倍的边

int n, m, mod;  // 点数、边数、取模的数
int h[N], hs[N], e[M], ne[M], idx;  // h: 原图；hs: 新图
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, scc_size[N];
int f[N], g[N];

void add(int h[], int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {
    
    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u, in_stk[u] = true;
    
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u]) {
        ++scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            scc_size[scc_cnt]++;
        } while (y != u);
    }
}

int main() {
    
    memset(h, -1, sizeof h);
    memset(hs, -1, sizeof hs);
    
    scanf("%d%d%d", &n, &m, &mod);
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(h, a, b);
    }
    
    // (1) 求SCC
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
    
    // (2) 缩点，建图
    unordered_set<LL> S;  // 判断是否为重边 (u, v) -> u * 1000000ll + v
    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];
            int a = id[i], b = id[k];
            LL hash = a * 1000000ll + b;
            if (a != b && !S.count(hash)) {
                add(hs, a, b);
                S.insert(hash);
            }
        }
    
    // (3) 根据拓扑序遍历DAG，从scc_cnt向前遍历自然满足拓扑序
    // 求解数组f和g
    for (int i = scc_cnt; i; i--) {
        if (!f[i]) {  // 说明是入度为0的点
            f[i] = scc_size[i];
            g[i] = 1;
        }
        for (int j = hs[i]; ~j; j = ne[j]) {
            int k = e[j];  // 边(i, k)
            if (f[k] < f[i] + scc_size[k]) {
                f[k] = f[i] + scc_size[k];
                g[k] = g[i];
            } else if (f[k] == f[i] + scc_size[k])
                g[k] = (g[k] + g[i]) % mod;
        }
    }
    
    // (3) 求解答案
    int maxf = 0, sum = 0;  // 最大半连通子图节点数、对应方案数
    for (int i = 1; i <= scc_cnt; i++)
        if (f[i] > maxf) {
            maxf = f[i];
            sum = g[i];
        }
        else if (f[i] == maxf) sum = (sum + g[i]) % mod;
    
    printf("%d\n", maxf);
    printf("%d\n", sum);
    
    return 0;
}

AcWing 368. 银河

问题描述

• 问题链接：AcWing 368. 银河

  

分析

• 这一题和AcWing 1169. 糖果是一模一样的，代码粘贴过来可以通过该题。
• 这一题还可以通过使用SCC来求解，但是注意并不是所有的差分约束问题都可以会用SCC来求解。
• 这一题可以使用SCC求解，是因为这一题的图比较特殊。
• 依次分析题目中给的5个条件：

（1）$A==B⟺A\ge B,B\ge A$；

（2）$A<B⟺B\ge A+1$；

（3）$A\ge B⟺A\ge B$；

（4）$A>B⟺A\ge B+1$；

（5）$A\le B⟺B\ge A$；

• 另外这个题目还有一个隐含条件：每个小朋友都要分到糖果，因此$x\ge 1$。因此我们可以建立一个虚拟源点$x_0=0$，则有：$x_i\ge x_0+1，i=1,...,n$。
• 根据不等式$x_i\ge x_0+1$可以建立从0号点到任意点的边，边权为1，因为可以到达任意点，所以可以到达任意边。
• 这一题需要求解是否存在正环，如果不存在正环需要求解一下每个点到0号点的最短距离之和。
• 因为本题中所有的边权值都是大于等于0的，我们可以首先求出所有的强联通分量，只要SCC中存在至少一条边的边权为1，则说明该SCC包含正环，无解；当所有SCC中的边权都为0是，存在解，每个SCC中的点到0号点的距离相同，可以看成一个点，采用缩点的技巧；然后相当于在新图（DAG）上求解每个点到0号点的最长路，直接使用递推即可。
• 总结一下，本题的过程是（这一类的题目都是这个套路）：

（1）使用tarjan算法求SCC；

（2）缩点建图；

（3）依据拓扑序递推；

• 需要建立的边数：如果K取$10^5$，所有的条件都是（1），需要$2\times 10^5$条边，同时还要从虚拟源点建立边，需要$10^5$条，因此一共需要$3\times 10^5$条边。又因为需要建新图，需要$6\times 10^5$。
• 另外如果每颗恒星的亮度是单调递增的，则结果可能爆int，因此需要使用long long存储结果。

代码

• C++

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, M = 600010;

int n, m;
int h[N], hs[N], e[M], w[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, sz[N];
int dist[N];  // 最长路径

void add(int h[], int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {
    
    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u, in_stk[u] = true;
    
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }
    
    if (low[u] == dfn[u]) {
        ++scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            sz[scc_cnt]++;
        } while (y != u);
    }
}

int main() {
    
    memset(h, -1, sizeof h);
    memset(hs, -1, sizeof hs);
    
    scanf("%d%d", &n, &m);
    while (m--) {
        int t, a, b;
        scanf("%d%d%d", &t, &a, &b);
        if (t == 1) add(h, a, b, 0), add(h, b, a, 0);
        else if (t == 2) add(h, a, b, 1);
        else if (t == 3) add(h, b, a, 0);
        else if (t == 4) add(h, b, a, 1);
        else add(h, a, b, 0);
    }
    
    for (int i = 1; i <= n; i++) add(h, 0, i, 1);
    
    // (1) 0号点可以到所有点
    tarjan(0);
    
    // (2) 缩点建图
    bool success = true;  // 代表是否存在解
    for (int i = 0; i <= n; i ++ ) {
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];
            int a = id[i], b = id[k];
            if (a == b) {
                if (w[j] > 0) {
                    success = false;
                    break;
                }
            } else add(hs, a, b, w[j]);
        }
        if (!success) break;
    }
    
    // (3) 依据拓扑序递推
    if (!success) puts("-1");
    else {
        for (int i = scc_cnt; i; i--)
            for (int j = hs[i]; ~j; j = ne[j]) {
                int k = e[j];
                dist[k] = max(dist[k], dist[i] + w[j]);
            }
        
        LL res = 0;
        for (int i = 1; i <= scc_cnt; i++) res += (LL) dist[i] * sz[i];
        
        printf("%lld\n", res);
    }
    
    return 0;
}