深度学习阶段性回顾
本文针对过去两周的深度学习理论做阶段性回顾,学习资料来自吴恩达老师的2021版deeplearning.ai课程,内容涵盖深度神经网络改善一直到ML策略的章节。视频链接如下:吴恩达深度学习视频链接
(注:本文出自深度学习初学者,此文内容将以初学者的感悟与见解讲述。当然我也会努力搜寻资料以弥补自身认知的不足,希望本文能对深度学习的其他初学者也有所帮助,文章若有不当之处,望大家在评论区多多指正,我将虚心接纳,多谢!)
Charpter1: 改善神经网络
1.训练集,开发集,测试集
深度学习的关键组成部分是神经网络,而神经网络具有深层次的网络结构,是一种依靠大量数据样本,通过正向传播、逆向传播算法对数据进行训练与学习,进而提取复杂数据特征与模式,从而完成指定任务的计算模型。正如小孩子通过体察世界、阅读书籍等方式认知世界,机器的学习也需要借助学习原料,这些原料就是大量的样本数据。(注:已有了解的同学可跳过段)
模型构建的过程常包括模型的训练,模型参数的调整以及模型的精确度检验,对应的所需数据集合成为训练集,开发集与测试集。
1.1三个数据集的基本概念
训练集指构建深度学习模型的数据集,机器需要依靠大量数据来识别与认知这个世界,而训练集就是机器的学习材料,使机器学习与认识输入数据与对应数据的标签输出之间的关系,让模型不断通过优化迭代算法,调节模型的参数与权重,最大限度地减少模型在训练集上地训练误差。
开发集用于调节与选择模型的超参数与结构,机器在开发集上进行模型选择、调整和验证,评估模型的性能、进行参数调优,并避免对训练集的过拟合,对于模型构建起到关键的评估与选择的作用,从而提高模型在测试集上的泛化能力。
测试集用于最终评估模型的性能与泛化能力,衡量模型在真实环境下的效果与实际的预测能力。
三个数据集往往相互独立,如果机器也能参加高考,那么三个数据集的作用比喻为:训练集是机器学习的学习原材料,用于学习知识点与掌握考点;然而单凭学习还不足以证明你有所掌握,此时开发集就是检验你学习效果的模拟考试,机器在模拟考试之后也会查漏补缺(对应为模式选择与参数调优等操作),从而扩充与巩固知识点;测试集便是机器的高考,用于检验“高中三年”学习训练的最终效果。若成绩优良,那自然是皆大欢喜,否则只能含泪复读了(重新训练或则调节参数)。
1.2 偏差与方差
偏差与方差是机器学习中的两个重要概念,用于衡量机器在训练样本与新样本上的预测效果,与欠拟合与过拟合之间存在着密切的关系。
偏差是指模型对于训练样本的预测值与真实值之间的差距,比如猫识别器识别一张猫图为非猫图,则称预测结果与真实值不符,存在偏差。高偏差通常意味着模型未能提取数据中的特征与模式,无法对数据的真实分布进行准确建模,导致欠拟合问题。
方差是指模型预测结果的变化程度,它反映了模型对训练数据的敏感性和抗干扰能力,方差较高的模型对训练集的小波动过度敏感,可能过度拟合训练数据中的噪声。低偏差与高方差的模型可能表现出良好1的拟合能力,当新数据上的泛化能力较差,导致过拟合。
2.欠拟合与过拟合
2.1判别拟合的方法
判别模型的拟合类别比较简单,欠拟合的判断方法是看模型在训练集上的预测值与真实值上的差距,如果差距较大,出现了高偏差,那么说明模型出现了欠拟合问题,模型还没能提取出数据的复杂特征模式。
判断过度拟合的方式是,在模型出现低偏差的条件下,看模型是否在新的数据集上出现高方差,即模型虽然能够很好地拟合训练集上的数据,但对于新数据缺乏拟合能力,谓之模型出现了过拟合问题。可见,新数据可来源于开发集与测试集。
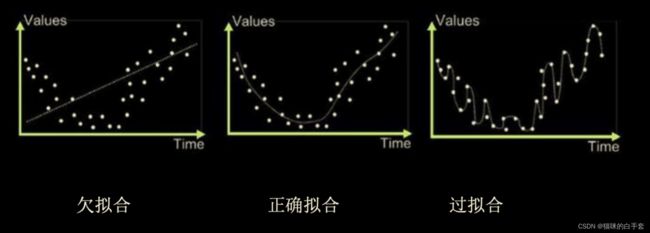
2.2 欠拟合与过拟合的图解
(注:图片来源于博客http://t.csdn.cn/lNUAn)
上图展示构建曲线拟合数据样本点的特征,曲线一出现欠拟合问题,模型无法拟合训练样本的数据特征,预测值与真实值存在高偏差(高误差),即模型出现欠拟合;曲线二则是恰当的拟合曲线,即模型能够提取数据的模式并拟合出数据样本的总体特征;曲线三出现了过拟合问题,模型学习训练集时学得过于精细了(曲线经过了训练数据的所有点),过度适应了训练数据集合,导致模型在新的数据上缺乏预测能力。
2.3解决方法
解决欠拟合的方法有:增加模型复杂度、引入更多特征、增加训练数据量等;
解决过拟合的方法有:降低模型复杂度、增加正则化技术、增加训练数据等,以下将着重讲解正则化技术。
3.正则化技术
正则化技术的用途在于解决模型的过拟合问题,而模型的过拟合问题常常来源于训练数据不足、模型网络过于复杂(学习能力太强了)、模型参数过多且权重过大、数据特征选择不当、数据标注错误、训练时间过长等原因,以下将讲解正则化技术是如何解决过拟合问题。
(注:本人对于正则化技术的理解来源于这位大佬的博客http://t.csdn.cn/TfZF0,所谓站在巨人的肩膀上才能学得更快,感兴趣的同学可以通过该博客了解正则化技术,本博客毕竟也只是初学者的见解!)
3.1 L1正则化
3.1.1 公式解释
![]() 正则化通过在损失函数中添加模型参数绝对值之和的惩罚项,将大部分参数压缩为0,从而实现特征选择和稀疏性。它倾向于生成稀疏权重向量,可以用于特征选择,即通过减小不相关的特征的权重使其趋近于0.
正则化通过在损失函数中添加模型参数绝对值之和的惩罚项,将大部分参数压缩为0,从而实现特征选择和稀疏性。它倾向于生成稀疏权重向量,可以用于特征选择,即通过减小不相关的特征的权重使其趋近于0.
![]() 正则化的损失函数:
正则化的损失函数:![]()
![]() 正则化的参数偏导:
正则化的参数偏导:![]()
新的损失函数在原损失函数的基础上添加了参数绝对值之和的惩罚项,其中![]() 是惩罚系数,
是惩罚系数,![]() 越大,惩罚就越狠。由于模型在梯度下降算法下,以损失函数最小化为目标,而新添的参数绝对值之和会增大损失函数,这意味着模型在训练的过程中,倾向于把参数变小。而参数代表模型对于数据某个特征赋予的权重,当损失函数渴望变小的同时保留对于训练数据的拟合能力,那么它就只能保留那些最重要且最能概括训练数据特征的参数权重,其余代表复杂特征的参数权重统统置为0(或很小值),从而提高了模型的泛化能力,解决了过拟合问题。
越大,惩罚就越狠。由于模型在梯度下降算法下,以损失函数最小化为目标,而新添的参数绝对值之和会增大损失函数,这意味着模型在训练的过程中,倾向于把参数变小。而参数代表模型对于数据某个特征赋予的权重,当损失函数渴望变小的同时保留对于训练数据的拟合能力,那么它就只能保留那些最重要且最能概括训练数据特征的参数权重,其余代表复杂特征的参数权重统统置为0(或很小值),从而提高了模型的泛化能力,解决了过拟合问题。
3.1.2举个栗子
举个例子(当然大佬那篇博客的例子也很不错,本人的例子不愿看可直接跳过),假设我们需要训练一个猫识别器,且为了简化问题只考虑猫的毛色与形态两个特征。我们知道凡是猫都具有普遍的形态:体型小,全身毛被密而柔软,锁骨小,吻部短,眼睛圆,颈部粗壮,四肢较短,足下有数个球形肉垫,舌面被有角质层的丝状钩形乳突等等;但猫的毛色却不尽相同,有白,黄,棕等等,屈指难数,如下为一些不同毛色猫猫的图片:
当我们的训练样本较少(假设只有上面四张图片)且网络结构较复杂(识别复杂特征的能力较强)时,模型同时记住猫的形态与这些猫的各种肤色,此时便出现了过拟合。它会认为只有当新测试样本(假设也是一猫但它的肤色不属于上述任意一种)满足猫的形态且猫的肤色满足上述四种颜色时,这个测试样本才会被判断为猫。由于新样本的肤色特征不符合模型要求,所以它被错判为非猫了。
为了解决这种过拟合问题,我加入惩罚项,迫使模型忘记数据的复杂特征,而只记住普遍特征,于是机器就思考:由于猫的肤色各不相同,若学习这些肤色特征需要消耗大量成本(给每个复杂特征对应的参数赋予高权重,导致损失函数数值过大),但如果只单独学习猫的形态其实便能判断一个动物是否猫,因此它单独学习猫的形态这一猫的普遍特征,因而当新的猫图输入时便能很自然被机器判断为猫啦!
3.1.3 L1正则化求解稀疏解
关于L1正则化是如何产生稀疏解的疑问,我觉得大佬的那篇博客已经解释得够清楚,而本人由于数学能力有限在此也难做解释,但也可以给出一些我的思考:由于模型训练的本质就是调节参数,而损失函数是关于参数的函数,训练目的在于找到损失函数的最优解。当我们限定参数的绝对值之和为一个定值时,由于训练参数较多,高维参数的绝对值之和为定值在高维空间中的图像是某个高维的几何体,几何体的端点比较突出,往往容易触碰到损失函数的最优解领域,从而对于参数向量![]() 只有少部分分量大于0,而大部分分量等于0,因而得到稀疏解。(注:本人也自觉解释得不到位,恰当的解释还是建议看大佬的博客,或者也可以参考这篇博客:http://t.csdn.cn/9bjhl)
只有少部分分量大于0,而大部分分量等于0,因而得到稀疏解。(注:本人也自觉解释得不到位,恰当的解释还是建议看大佬的博客,或者也可以参考这篇博客:http://t.csdn.cn/9bjhl)
3.2 L2正则化
![]() 正则化通过在损失函数中添加模型参数平方和的惩罚项,限制模型参数的值域大小。
正则化通过在损失函数中添加模型参数平方和的惩罚项,限制模型参数的值域大小。![]() 正则化会使模型的参数接近于0,但不等于0,因此不会得到稀疏权重向量。它对异常值的敏感度较低,可以有效地防止过拟合。
正则化会使模型的参数接近于0,但不等于0,因此不会得到稀疏权重向量。它对异常值的敏感度较低,可以有效地防止过拟合。
3.2.1 公式解释
![]() 正则化损失函数:
正则化损失函数:![]()
![]() 正则化参数偏导:
正则化参数偏导:![]()
关于![]() 正则化如何通过惩罚项解决正则化问题,其道理与
正则化如何通过惩罚项解决正则化问题,其道理与![]() 正则化解决过拟合问题的道理是互通的,在此不多加解释。
正则化解决过拟合问题的道理是互通的,在此不多加解释。
3.2.2  与
与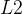 正则化的区别
正则化的区别
- 计算方式的不同:两者在损失函数与参数偏导上的所添加的公式不同;
- 参数限制程度:
 正则化鼓励模型的参数稀疏性,即通过将一部分参数的权重推向零来减少特征的依赖性;
正则化鼓励模型的参数稀疏性,即通过将一部分参数的权重推向零来减少特征的依赖性;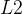 正则化更倾向于将参数权重均匀地减小,但不会强制将其推向零。L2正则化会使得模型的参数权重趋向于较小的值,但不会稀疏参数;
正则化更倾向于将参数权重均匀地减小,但不会强制将其推向零。L2正则化会使得模型的参数权重趋向于较小的值,但不会稀疏参数; - 形状:
 正则化项形状是由参数的绝对值之和构成的一个等边矩形(L1范数的等值线为菱形),其对应的正则化项的图像为“角”状;
正则化项形状是由参数的绝对值之和构成的一个等边矩形(L1范数的等值线为菱形),其对应的正则化项的图像为“角”状;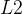 正则化的正则化项形状是由参数的平方和的平方根构成的一个球体(L2范数的等值线为圆),其对应的正则化项的图像为“球”状;
正则化的正则化项形状是由参数的平方和的平方根构成的一个球体(L2范数的等值线为圆),其对应的正则化项的图像为“球”状;
3.3 Dropout正则化
Dropout是一种特殊的正则化技术,其基本思想是在训练过程中以一定的概率丢弃(置零)随机选择的隐藏层单元。这样可以防止某些特征值过度依赖于特定的隐藏单元,并促使模型学习到多个独立的特征表示。通过随机丢弃隐藏层单元,正则化抑制可以减少模型对特定训练样例的过度依赖,从而提高泛化能力和鲁棒性.
3.3.1 python代码实现
Dropout的正向传播代码:
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
#原文有缩进问题,请注意!
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines)
# Steps 1-4 below correspond to the Steps 1-4 described above.
# Step 1: initialize matrix D1 = np.random.rand(..., ...)
#rand是随机生成0~1之间的数
D1 = np.random.rand(A1.shape[0],A1.shape[1])
# Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
D1 = D1Dropout的逆向传播代码实现:
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
### START CODE HERE ### (≈ 2 lines of code)
# Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2*D2
# Step 2: Scale the value of neurons that haven't been shut down
dA2/=keep_prob
### END CODE HERE ###
#确保A2大于0
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
### START CODE HERE ### (≈ 2 lines of code)
# Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1*D1
# Step 2: Scale the value of neurons that haven't been shut down
dA1/=keep_prob
### END CODE HERE ###
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients代码来源于吴恩达的课后编程作业,上述代码实现对3层神经网络实施dropout操作。注意dropout在每一次迭代时会抛弃一部分神经元,被遗弃的神经元无需进行正向传播与逆向传播。
3.4 过拟合的原因解释
有了对于L1正则化如何解决过拟合问题的认识,便能很好地解释出现过拟合原因的所以然,过拟合原因的解释如下:
- 训练数据不足:训练数据不足的反面是训练数据充足,众所周知,模型的训练数据量越大,模型的预测能力越强,泛化能力也越强,为什么呢?第一,训练数据的增多意味着数据多样性的增多,模型自然能见多识广,捕捉罕见样本,涵盖更广泛的场景;第二,当模型的复杂程度一定时,它学习特征与模式的能力也有限,当数据量很大时,模型自然无法对每个数据进行精细化的学习,为了降低损失函数数值,它只能在大量的数据中学习样本的普遍特征,就好比如当样本中有上亿种猫的肤色时,模型学习这种特定特征的能力就有限了,因为它觉得去学习普遍特征更加值得,从而模型的泛化能力较强。反之亦然,当训练的数据量较少时,模型便容易出现过拟合现象,道理都是互通的。(注:此处内容来源于在阅读其他资料后思考得出的见解)
- 模型网络过于复杂:同理,当思考复杂的模型网络会引发过拟合前,,也需要控制其他变量,当数据量一定时,模型网络结构过于复杂,它的特征识别能力也就过强了。(例如,小样本训练复杂模型)当机器“学有余力”时,它便会去提取数据特定的特征(例如,去学习猫的肤色),过度适应训练样本,导致在新数据上缺乏泛化能力。
- 模型参数过多且权重过大:道理都是互通的,当模型参数过多且权重过大时往往意味着模型网络结构过于复杂,自然会导致过拟合。
- 数据特征选择不当:道理都是互通的,训练时模型选择了不当的特征,比如选择了事物的非普遍性特征,便会在预测新数据时出现过拟合问题。